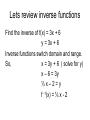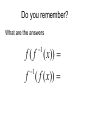Download 4.7 Inverse Trigonometric fucntions

4.7 Inverse Trigonometric
functions
Arcsine
Arccosine
Lets review inverse functions
Find the inverse of f(x) = 3x + 6
y = 3x + 6
Inverse functions switch domain and range.
So,
x = 3y + 6 ( solve for y)
x – 6 = 3y
⅓x–2=y
f -1(x) = ⅓ x - 2
What is the domain and range of
the Sine function
Domain: All real numbers
Range: - 1 to 1
What is the domain and range of
the Inverse of the Sine function
The inverse’s Domain would be -1 to 1; Yet
the Range is not all real numbers.
Range
 

1, 


 2
2
2
y
2
1
 

  1,

2 

1

2
Inverse of the Cosine
Domain: [ -1,1]
Range: [ ,0]
 1,  
1,0
The Tangent function

Domain: All real numbers except  n
2
Where n is a integer
Range: All real numbers
Inverse of Tangent function
Domain: All real numbers



y

Range: 2
2
Definition of Arcsine
The arc sine is the inverse function of the
sine. What is the angle that has a sine
equal to a given number 2
arcsin
2
2



4
2
Since, sin 
4
2
2
Solve
Find the exact value.
For these problems
All answers are in the
First Quadrant.
3
arccos

2
1
arcsin 
2
arctan 1 
Solve
Find the exact value.
For these problems
All answers are in the
First Quadrant.
3 
arccos

2
6
1 
arcsin 
2 6
arctan 1 

4
Do you remember?
What are the answers
1
f ( f ( x)) 
1
f ( f ( x)) 
Solve
Be careful to make sure it is in the Range
 
arcsin  sin  
3

7

arccos cos
6




Solve
Be careful to make sure it is in the Range
  
arcsin  sin  
3 3

7

arccos cos
6

 5

 6
For the arccos the range is [ ,0]
So
arccos(cos x)  0
for[0,  ]
Solve using a triangle
Cot(arctan x)
Let arctan x = u
x2 1
x
u
1
1
Cot u =
x
Solve
Let
x 

csc arctan

2

u  arctan
x
2
, then tan u 
x
2
x2  2
x
u
2
Solve
x 

csc arctan

2

So csc u  1
sin u
sin u 
csc u 
x
x2  2
x2  2
x
1
x
x2  2
u
2
csc u 
x2  2
x
Show that
36  x 2
x
arcsin
 arccos
6
6
Show that
36  x 2
x
arcsin
 arccos
6
6
Using arccos
x ?  6
2
2
6
2
?2  36  x 2
?  36  x
2
?
u
x
Show that
36  x 2
x
arcsin
 arccos
6
6
Using arccos
x ?  6
2
2
6
2
?2  36  x 2
?  36  x
2
36  x 2
u
x
36  x
sin u 
6
x
cos u 
6
2
Homework
Page 328 – 331
# 1, 5, 9, 13, 16,
21, 27, 33, 40,
44, 51, 61, 66,
74, 85, 94, 104,
110, 122
Homework
Page 328 – 331
# 3, 8, 12, 15, 18,
24, 30, 37, 41, 47,
56, 65, 71, 83, 91,
96, 107, 121