Download Unit 11 – Exponential and Logarithmic Functions

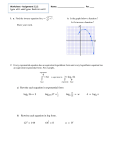
Unit 11 – Exponential and Logarithmic Functions
Unit 11.1 Inverse Functions
We are going to look at exponential functions and logarithmic functions in this unit. For example
f  x   5x is an exponential function and f  x   log3 x is a logarithmic function.
These functions relate to each other. They are inverses of each other. So let’s look at inverse
functions first.
Review:
Define domain: all the inputs, the x values
Define range: all the outputs, the y values
Give an example of a function with an unlimited domain (i.e. all real numbers): f  x   3x  2
1
f  x 
x  2 the
Give an example of a function with a limited domain. What is it’s limitation?:
number -2 is not in the domain as it makes the denominator zero and thus the function is
undefined.
What is the range of the two example functions: the range of the first function is all real numbers
and the range of the second is all real numbers with the exception of zero.
One-to-One functions: In a one-to-one function, each x-value corresponds to only one y-value,
and each y-value corresponds to just one x-value.
What is the difference between this definition and the definition of a function we talked about
earlier this year? A function only requires that each x-value have one and only one y-value. A yvalue may “belong” to more than one x-value. This is not true in a one-to-one function.
Only one-to-one functions have an inverse.
Let’s define function G   2, 2  ,  1,1 ,  0,0  , 1,3 ,  2,5
If we interchange the x and y values we get the inverse of function G.
F   2, 2  , 1, 1 ,  0,0  ,  3,1 , 5, 2 
Because we interchange the x and y values to get the inverse, it follows that the domain of the
original function is the range of the inverse and the range of the original function becomes the
domain of the inverse.
The function notation for inverse functions is f 1  x   . Notice that once again we are using
notation that looks like something else. You’re just going to have to go by the context of the
problem. In this context we are looking at an inverse function, not a negative exponent.
To find an inverse function you first have to determine if the function is a one-to-one function. If
it isn’t, then it doesn’t have an inverse and you can stop looking!
Example:
F   2,1 ,  1,0  ,  0,1 , 1, 2  ,  2, 2 
This is not a one-to-one function because the y-value 2 corresponds to two x-values. No inverse.
582707646
Page 1 of 8
Unit 11 – Exponential and Logarithmic Functions
G   3,1 ,  0, 2  ,  2,3 ,  4,0  is a on-to-one function and thus has an inverse
G 1  1,3 ,  2,0  ,  3, 2  ,  0, 4 
Horizontal Line Test:
We use a Vertical Line Test to help us determine if a particular equation is a function. In a
similar fashion we use a Horizontal Line Test to help us determine if a particular equation is a
one-to-one function. If every horizontal line intersects the graph of the function at only one point
then the function is a one-to-one function. (Note the equation has to first pass the vertical line
test and be a function.
Examples to put on board:
Finding the equation of the inverse of a function
1.
2.
3.
4.
Rewrite the function notation as a “y =” form of equation.
Interchange the y and the x.
Solve for y.
Rewrite in inverse function notation by replacing the y with f 1  x  
Example: Use the function from above f  x   3x  2 .
y  3x  2
1. Rewrite as “y =”
2. Interchange the y and the x x  3 y  2
x  3y  2
x  3 y  2
3. Solve for y 3 y   x  2
3y  x  2
y
x2
3
4. Rewrite in inverse function notation
f  1 x  
x2
3
Examples:
2.
x4
3
1
3
3
f  x   x  1 inverse is f  x   x  1
3.
f  x    x  3 there is no inverse this is not a one-to-one function. Why not?
1.
582707646
f  x   3x  4 inverse is f 1  x  
2
Page 2 of 8
Unit 11 – Exponential and Logarithmic Functions
An inverse function “undoes” it’s related function. One way to look at this is you will end up
back where you started. For example, plug a number into the function in #1 above, take the
output and plug it into the inverse. What do you get?
Unit 11.2 – Exponential Function
For a > 0 and a  1 and all real numbers x, f  x   a x defines the exponential function with base
a.
Graph f  x   2x (blue line) and f  x   5x (green line)
This graph is typical of exponential functions where a > 1. The larger the value of a the faster
the graph rises.
x
x
1
1
Graph f  x     (blue line) and f  x     (green line)
2
5
Here as x gets larger y gets smaller.
Characteristics of the graph of f  x   a x
1. The graph contains the point (0, 1).
2. If a > 1 the graph rises from left to right. If 0 < a < 1, the graph falls from left to right. Both
go from 2nd to 1st quadrants.
3. The x-axis is an asymptote.
4. The domain is  ,   and the range is  0,   .
582707646
Page 3 of 8
Unit 11 – Exponential and Logarithmic Functions
What happens when you graph a more complicated exponential function such as f  x   32 x 4 ?
(Very similar to f  x   3x except it is shifted to the right and rises more rapidly.)
How would we solve 9 x  27 ?
Property for solving an exponential Equation
For a > 0 and a  1, if a x  a y then x  y .
Solving an Exponential Equation
1. Each side must have the same base. If the two sides do not have the same base, express each
as a power of the same base.
2. Simplify exponents, if necessary, using the rules of exponents.
3. Set exponents equal using the exponential equation property.
4. Solve the equation from Step 3.
(Note: for equations such as 3x  12 we need to use a different method because Step 1 is difficult
to do.)
Example:
9 x  27
3 
2
x
 33 write with the same base (step 1)
32 x  33 simplify exponents with the power rule (step 2)
2 x  3 set exponents equal (step 3)
3
x  solve for x (step 4)
2
Examples: 25x  125
4 x  32
81x  27
Unit 11.3 Logarithmic Functions
What is a logarithm?
A logarithm is an exponent. Remember in the previous unit I said that we couldn’t solve 3x  12
because it is difficult to express both sides of the equation as expressions with the same base?
Well, there are ways to use logarithms to solve equations such as this. (We’ve got a ways to go
before we’re ready for that. (check page 695)).
Logarithm
For all positive numbers a, with a  1, and all positive numbers x,
y  log a x means the same as x  a y . This is saying the expression log a x represents the
exponent to which the base a must be raised in order to get x.
582707646
Page 4 of 8
Unit 11 – Exponential and Logarithmic Functions
Exponential Form
Logarithmic Form
32  9
log 3 9  2
2
1
   25
5
105  100, 000
log 1 25  2
5
log10100, 000  5
1
64
5
2  32
1
 3
64
log 2 32  5
1
log10010  1
43 
100
8
2
3
2
log 4
 10
4
64 
log8 4  2
1
1296
log 6
2
3
1
 4
1296
Solving logarithmic equations
log 4 x  2
42  x rewrite as exponential equation using the definition of a logarithm
1
x 2
4
1

16
log 1  3x  1  2
2
2
1
   3x  1 rewrite as an exponential equation
2
1
3x  1 
4
12 x  4  1 multiply both sides by 4 to get rid of the fraction
12 x  3
1
x
4
log x 3  2
x2  2
x  3 only the principal root since the base must be a positive number
582707646
Page 5 of 8
Unit 11 – Exponential and Logarithmic Functions
log 49 3 7  x
49 x  3 7
7 
2
x
7
72 x  7
1
2x 
3
6x  1
1
x
6
1
1
3
3
For any positive real number b, with b  1,
logbb  1
logb1  0
Unit 11.4 Properties of Logarithms
Product Rule for Logarithms
log b xy  log b x  log b y The logarithm of a product is equal to the sum of the logarithms of the
factors.
Proof of the Product Rule
let m  log b x and n  log b y and remember that
log b x  m means b m  x
log b y  n means b n  y
therefore
xy  b m  b n substitution
xy  b m  n product rule for exponents
log b xy  m  n convert to logarithmic form
log b xy  log b x  log b y substitution
Examples:
log5  6  9  log5 6  log5 9
log7 8  log712  log7 96
log3  3x   log3 3  log3 x make sure they understand what log3 3 equals and why
=1+log3 x
582707646
Page 6 of 8
Unit 11 – Exponential and Logarithmic Functions
log 4 x3  log 4  x  x  x 
 log 4 x  log 4 x  log 4 x
 3log 4 x
log 6  5  8   log 6 5  log 6 8
log 4 3  log 4 7  log 4 21
log8 8 x  log8 8  log8 x  1  log8 x
log 5 m 2  2log 5 m
Quotient Rule for Logarithms
If x, y, and b are positive real numbers, where b  1, then
x
logb  logb x  logb y The logarithm of a quotient is the difference between the logarithm of the
y
numerator and the logarithm of the denominator.
Examples:
7
log 4  log 4 7  log 4 9
9
6
log 5 6  log 5 x  log 5 ? any restrictions on x?
x
27
log3
 log3 27  log3 5
this illustrates an important point. When solving logs, if you can
5
 3  log3 5
convert a log to a number then do so.
Power Rule for Logarithms
If x and b are positive real numbers, where b  1, and if r is any real number, then
log b x r  rlog b x
Recall this example from the Product Rule:
log 4 x3  log 4  x  x  x 
 log 4 x  log 4 x  log 4 x
 3log 4 x
Examples:
log 5 42  2log 5 4
logb 7 when using the power rule with logarithms of expressions involving radicals, first
rewrite the radical expression with a rational exponent.
log b 7  log b 7
1
2
1
 log b 7
2
582707646
Page 7 of 8
Unit 11 – Exponential and Logarithmic Functions
log 2 5 x 2  log 2 x
2
5
2
log 2 x
5
log 3 52  2log 3 5

1
log b 8
2
1
log 2 3 2 
3
log b 8 
Special Properties of Logarithms
If b > 0 and b  1, then
blogb x  x and log bb x  x
The second is the easiest to understand.
To prove the first property:
y  logb x
Let b y  x convert to exponential form
blogb x  x replace y with logb x
Properties of Logarithms
logb xy  logb x  logb y
Product Rule
logb
Quotient Rule
Power Rule
x
 logb x  logb y
y
logb xr  rlogb x
blogb x  x and log bb x  x
Special Properties
Writing Logarithms in Alternative Forms
log 4 4 x3  log 4 4  log 4 x3
 1  3log 4 x
log 7
m
m
 log 7  
n
n
1
2
1
m
log 7  
2
n
1
  log 7 m  log 7 n 
2

582707646
Page 8 of 8