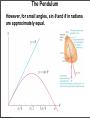
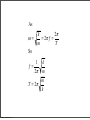* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Biofluid dynamics wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Brownian motion wikipedia , lookup
Reynolds number wikipedia , lookup
Classical central-force problem wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Equations of motion wikipedia , lookup
Mass versus weight wikipedia , lookup
Centripetal force wikipedia , lookup
Seismometer wikipedia , lookup
Hunting oscillation wikipedia , lookup
Fluid dynamics wikipedia , lookup
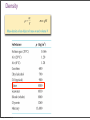
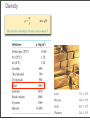
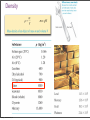
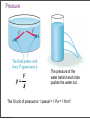
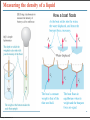
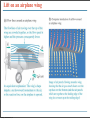
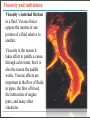
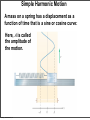
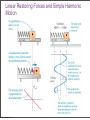
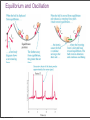
Fluids Monday, November 28, 11 Monday, November 28, 11 Density m = ρV Monday, November 28, 11 Density m = ρV Monday, November 28, 11 Density m = ρV Monday, November 28, 11 Density m = ρV Monday, November 28, 11 Pressure The pressure of the water behind each hole pushes the water out. The SI unit of pressure is 1 pascal = 1 Pa = 1 N/m2. Monday, November 28, 11 Monday, November 28, 11 Monday, November 28, 11 Pressure in a Liquid Increases with Depth Monday, November 28, 11 Pascal’s Law Pressure is everywhere equal in a uniform fluid of equal depth. Monday, November 28, 11 Pascal’s Law Pressure is everywhere equal in a uniform fluid of equal depth. Monday, November 28, 11 Pascal’s Law Pressure is everywhere equal in a uniform fluid of equal depth. F1 F2 = A1 A2 Monday, November 28, 11 Monday, November 28, 11 Blaise Pascal (June 19, 1623 – August 19, 1662) Pascal was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father. Pascal's earliest work was in the study of fluids, and clarified the concepts of pressure and vacuum by generalizing the work of Evangelista Torricelli. Pascal also wrote in defense of the scientific method. Monday, November 28, 11 Weight of air on your hand Monday, November 28, 11 Weight of air on your hand Your hand has an area of approximately 150 cm2, atmospheric pressure is 103,000 Pa, what is the mass of the air pressing down on your hand? Monday, November 28, 11 Weight of air on your hand Your hand has an area of approximately 150 cm2, atmospheric pressure is 103,000 Pa, what is the mass of the air pressing down on your hand? F 150 P = ⇒ F = PA = 103000 × = 154.5N A 10000 F 154.5 F = mg ⇒ m = = ≈ 15.8kg g 9.8 Monday, November 28, 11 Weight of air on your hand Your hand has an area of approximately 150 cm2, atmospheric pressure is 103,000 Pa, what is the mass of the air pressing down on your hand? F 150 P = ⇒ F = PA = 103000 × = 154.5N A 10000 F 154.5 F = mg ⇒ m = = ≈ 15.8kg g 9.8 Why don’t you notice this? Monday, November 28, 11 Weight of air on your hand Your hand has an area of approximately 150 cm2, atmospheric pressure is 103,000 Pa, what is the mass of the air pressing down on your hand? F 150 P = ⇒ F = PA = 103000 × = 154.5N A 10000 F 154.5 F = mg ⇒ m = = ≈ 15.8kg g 9.8 Why don’t you notice this? The same pressure is also pushing up under your hand. Monday, November 28, 11 Monday, November 28, 11 Monday, November 28, 11 Absolute Pressure & Gauge Pressure What is the pressure inside a flat tire? Monday, November 28, 11 Absolute Pressure & Gauge Pressure What is the pressure inside a flat tire? Atmospheric pressure Monday, November 28, 11 Absolute Pressure & Gauge Pressure What is the pressure inside a flat tire? Atmospheric pressure So when we see a tire wall that says inflate to 32 lb/in2 (220 kPa), this means that the difference between the pressure inside the tire and outside the tire needs to be 32 lb/in2 greater than atmospheric pressure. So the total pressure inside the tire is atmospheric pressure 14.7 lb/in2 (103 kPa) plus 32 lb/in2 (220 kPa), this gives a total pressure of 47 lb/in2 (323 kPa). Monday, November 28, 11 Monday, November 28, 11 Finding absolute and gauge pressure By Pascal’s law Pressure to be measured, p Monday, November 28, 11 There are many clever ways to measure pressure Monday, November 28, 11 There are many clever ways to measure pressure Monday, November 28, 11 Monday, November 28, 11 Buoyancy and Archimedes Principle Monday, November 28, 11 Buoyancy and Archimedes Principle Monday, November 28, 11 Buoyancy and Archimedes Principle Bouyant Force, FB = ρ f V f g Monday, November 28, 11 Buoyancy and Archimedes Principle • The buoyant force is equal to the weight of the displaced fluid. Bouyant Force, FB = ρ f V f g Monday, November 28, 11 Monday, November 28, 11 A floating object is in static equilibrium. Monday, November 28, 11 A floating object is in static equilibrium. Monday, November 28, 11 Measuring the density of a liquid Monday, November 28, 11 Measuring the density of a liquid Monday, November 28, 11 Measuring the density of a liquid How a boat floats Monday, November 28, 11 How big does a ballon need to be? Monday, November 28, 11 Buoyancy and Archimedes Principle Monday, November 28, 11 Buoyancy and Archimedes Principle Volume of Statue Monday, November 28, 11 Buoyancy and Archimedes Principle Volume of Statue Weight of displaced seawater Monday, November 28, 11 Buoyancy and Archimedes Principle Volume of Statue Weight of displaced seawater When at rest net force is zero Monday, November 28, 11 Buoyancy and Archimedes Principle Volume of Statue Weight of displaced seawater When at rest net force is zero Monday, November 28, 11 Buoyancy and Archimedes Principle Weight of displaced air Monday, November 28, 11 Q14.1 The sphere on the right has twice the mass and twice the radius of the sphere on the left. Compared to the sphere on the left, the larger sphere on the right has A. twice the density. B. the same density. C. 1/2 the density. D. 1/4 the density. E. 1/8 the density. Monday, November 28, 11 mass m radius R mass 2m radius 2R A14.1 The sphere on the right has twice the mass and twice the radius of the sphere on the left. Compared to the sphere on the left, the larger sphere on the right has mass m radius R mass 2m radius 2R A. twice the density. B. the same density. C. 1/2 the density. D. 1/4 the density. E. 1/8 the density. Monday, November 28, 11 m m 2m ρ = , ρ1 = , ρ2 = 4 4 V 3 πR π (2R)3 3 3 m 4 3 π R ρ1 1 1 1 3 ⇒ = = = = 2m 2 1 1 ρ2 3 2 4 2 4 π (2R)3 2 3 Q14.2 A block of ice (density 920 kg/m3) and a block of iron (density 7800 kg/m3) are both submerged in a fluid. Both blocks have the same volume. Which block experiences the greater buoyant force? A. the block of ice B. the block of iron C. Both experience the same buoyant force. D. The answer depends on the density of the fluid. Monday, November 28, 11 A14.2 A block of ice (density 920 kg/m3) and a block of iron (density 7800 kg/m3) are both submerged in a fluid. Both blocks have the same volume. Which block experiences the greater buoyant force? A. the block of ice B. the block of iron C. Both experience the same buoyant force. D. The answer depends on the density of the fluid. Both displace same volume of water, hence same weight of water, hence both have the same buoyant force. Monday, November 28, 11 Q14.3 A cylinder is completely filled with water. The top of the cylinder is sealed with a tight-fitting lid. If you push down on the lid with a pressure of 1000 Pa, the water pressure at the bottom of the cylinder A. increases by more than 1000 Pa. B. increases by 1000 Pa. C. increases by less than 1000 Pa. D. is unchanged. E. The answer depends on the height of the cylinder. Monday, November 28, 11 A14.3 A cylinder is completely filled with water. The top of the cylinder is sealed with a tight-fitting lid. If you push down on the lid with a pressure of 1000 Pa, the water pressure at the bottom of the cylinder A. increases by more than 1000 Pa. B. increases by 1000 Pa. C. increases by less than 1000 Pa. D. is unchanged. E. The answer depends on the height of the cylinder. Monday, November 28, 11 Surface tension • How is it that water striders can walk on water (although they are more dense than the water)? The surface behaves like a membrane Monday, November 28, 11 Surface tension The cohesive forces among the liquid molecules are responsible for this phenomenon of surface tension. In the bulk of the liquid, each molecule is pulled equally in every direction by neighboring liquid molecules, resulting in a net force of zero. The molecules at the surface do not have other molecules on all sides of them and therefore are pulled inwards. This creates some internal pressure and forces liquid surfaces to contract to the minimal area. Monday, November 28, 11 Surface tension • Surface tension also explains why falling raindrops are spherical not tear drop shaped. A falling drop of water, filmed at 3000 images per second. Monday, November 28, 11 Fluid Flow Fluid flow can be very complex, as can be seen in the smoke from the match. Monday, November 28, 11 Ideal Fluid An Ideal Fluid is a fluid that is incompressible (its density does not change) and has no internal friction (called viscosity). Liquids are approximately incompressible in most situations. We can treat gases as incompressible only if the pressure change from one region to another is not too great. Internal friction in a fluid causes shear stresses when two adjacent layers of fluid move relative to each other, as when fluid flows around an obstacle. Monday, November 28, 11 An Ideal Fluid Monday, November 28, 11 Fluid flow Monday, November 28, 11 Fluid flow Monday, November 28, 11 Fluid flow Monday, November 28, 11 Monday, November 28, 11 Continuity Equation The mass of a moving fluid does not change as it flows, the mass remains constant. This leads to an important quantitative relationship called the continuity equation. ρ A1v1dt = ρ A2 v2 dt or A1v1 = A2 v2 is the continuity equation for incompressible flow dV Q= = Av is the volume flow rate dt dV ρ is the mass flow rate dt ρ1 A1v1dt = ρ2 A2 v2 dt is the continuity equation for compressible flow Monday, November 28, 11 Fluid flow Flow speed changes through a tapered pipe Monday, November 28, 11 Fluid flow The speed of the water is inversely proportional to the diameter of the stream. Monday, November 28, 11 Speed of water through a hose Monday, November 28, 11 Deriving Bernoulli’s The fluid is incompressible, so dV = A1ds1 = A2 ds2 The work done on this fluid element during dt F dW = p1 A1ds1 − p2 A2 ds2 (as W=Fs, P= ⇒ F = PA) A dW = ( p1 − p2 )dV As m = ρdV, the change in kinetic energy is 1 dK = ρdV (v22 − v12 ) 2 The change in gravitational potential energy is dU = ρdVg(y2 − y1 ) The energy equation tells us dW = dK + dU, so 1 2 2 ( p1 − p2 )dV = ρdV (v2 − v1 ) + ρdVg(y2 − y1 ) 2 1 2 2 p1 − p2 = ρ(v2 − v1 ) + ρ g(y2 − y1 ) this is Bernoulli's equation 2 Monday, November 28, 11 equation Pressure difference associated with change in speed of fluid 1 2 2 p1 − p2 = ρ(v2 − v1 ) + ρ g(y2 − y1 ) 2 Pressure difference associated caused by the fluid weight and the difference in elevation at the two ends Monday, November 28, 11 Pressure difference associated with change in speed of fluid 1 2 2 p1 − p2 = ρ(v2 − v1 ) + ρ g(y2 − y1 ) 2 Pressure difference associated caused by the fluid weight and the difference in elevation at the two ends Or can write as: Monday, November 28, 11 Pressure difference associated with change in speed of fluid 1 2 2 p1 − p2 = ρ(v2 − v1 ) + ρ g(y2 − y1 ) 2 Pressure difference associated caused by the fluid weight and the difference in elevation at the two ends Or can write as: Monday, November 28, 11 Pressure difference associated with change in speed of fluid 1 2 2 p1 − p2 = ρ(v2 − v1 ) + ρ g(y2 − y1 ) 2 Pressure difference associated caused by the fluid weight and the difference in elevation at the two ends Or can write as: Monday, November 28, 11 Water pressure in a home (Bernoulli’s Principle) Find speed at bathroom, v2, using the continuity equation Volume flow rate is Find pressure at bathroom, p2, using the Bernoulli’s equation Monday, November 28, 11 Speed of efflux (Bernoulli’s Equation) Apply Bernoulli’s equation to points 1 & 2 y2=h y1=0 Monday, November 28, 11 The Venturi meter (Bernoulli’s Equation) Apply Bernoulli’s equation noting that y1=y2 We know that the pressure difference (p1-p2) is ρgh, so substituting this in the above expression and rearranging for v1 Monday, November 28, 11 Lift on an airplane wing Monday, November 28, 11 Viscosity and turbulence Viscosity is internal friction in a fluid. Viscous forces oppose the motion of one portion of a fluid relative to another. Viscosity is the reason it takes effort to paddle a canoe through calm water, but it is also the reason the paddle works. Viscous effects are important in the flow of fluids in pipes, the flow of blood, the lubrication of engine parts, and many other situations. Monday, November 28, 11 Viscosity and turbulence When we cease to treat fluids as ideal, molecules can attract or repel one another—they can interact with container walls and the result is turbulence. Monday, November 28, 11 A curve ball (Bernoulli’s equation applied to sports) Bernoulli’s equation allows us to explain why a curve ball would curve, and why a slider turns downward. Slower higher pressure air Slower higher pressure air Faster lower pressure air Monday, November 28, 11 Faster lower pressure air A curve ball (Bernoulli’s equation applied to sports) Bernoulli’s equation allows us to explain why a curve ball would curve, and why a slider turns downward. Slower higher pressure air Slower higher pressure air Faster lower pressure air Monday, November 28, 11 Faster lower pressure air Q14.4 An incompressible fluid flows through a pipe of varying radius (shown in cross-section). Compared to the fluid at point P, the fluid at point Q has P radius R radius 2R A. greater pressure and greater volume flow rate. B. greater pressure and the same volume flow rate. C. the same pressure and greater volume flow rate. D. lower pressure and the same volume flow rate. E. none of the above Monday, November 28, 11 Q A14.4 An incompressible fluid flows through a pipe of varying radius (shown in cross-section). Compared to the fluid at point P, the fluid at point Q has P radius R radius 2R A. greater pressure and greater volume flow rate. B. greater pressure and the same volume flow rate. C. the same pressure and greater volume flow rate. D. lower pressure and the same volume flow rate. E. none of the above Monday, November 28, 11 Q Q14.5 An incompressible fluid flows through a pipe of varying radius (shown in cross-section). Compared to the fluid at point P, the fluid at point Q has P radius R radius 2R A. 4 times the fluid speed. B. 2 times the fluid speed. C. the same fluid speed. D. 1/2 the fluid speed. E. 1/4 the fluid speed. Monday, November 28, 11 Q A14.5 An incompressible fluid flows through a pipe of varying radius (shown in cross-section). Compared to the fluid at point P, the fluid at point Q has P radius R radius 2R A. 4 times the fluid speed. B. 2 times the fluid speed. C. the same fluid speed. D. 1/2 the fluid speed. E. 1/4 the fluid speed. A1 = π (2R)2 = 4π R 2 , A2 = π R 2 ⇒ A1 = 4A2 From continuity equation A1v1 = A2 v2 = 4A2 v1 v1 = 4v1 Monday, November 28, 11 Q Blood flow in capillaries Monday, November 28, 11 Blood flow in capillaries Monday, November 28, 11 Blood flow in capillaries Monday, November 28, 11 Simple Harmonic Motion, Pendulums Monday, November 28, 11 Introduction If you look to the right, you’ll see a time-lapse photograph of a simple pendulum. It’s a great example of the regular oscillatory motion we’re about to study. Monday, November 28, 11 Oscillations about Equilibrium Monday, November 28, 11 Monday, November 28, 11 Periodic Motion Period: time required for one cycle of periodic motion Frequency: number of oscillations per unit time 1 f = T This unit is called the Hertz: Monday, November 28, 11 Simple Harmonic Motion A mass on a spring has a displacement as a function of time that is a sine or cosine curve: Here, A is called the amplitude of the motion. Monday, November 28, 11 Simple Harmonic Motion A spring exerts a restoring force that is proportional to the displacement from equilibrium: Monday, November 28, 11 Simple Harmonic Motion A spring exerts a restoring force that is proportional to the displacement from equilibrium: Monday, November 28, 11 Simple harmonic motion An ideal spring responds to stretch and compression linearly, obeying Hooke’s Law. For a real spring, Hookes’Law is a good approximation. Monday, November 28, 11 Linear Restoring Forces and Simple Harmonic Motion Monday, November 28, 11 Monday, November 28, 11 Equilibrium and Oscillation Monday, November 28, 11 Monday, November 28, 11 Sinusoidal Relationships Monday, November 28, 11 Mathematical Description of Simple Harmonic Motion Monday, November 28, 11 Simple Harmonic Motion If we call the period of the motion T – this is the time to complete one full cycle – we can write the position as a function of time: ⎛ 2π ⎞ x = A cos ⎜ t⎟ ⎝ T ⎠ It is then straightforward to show that the position at time t + T is the same as the position at time t, as we would expect. Monday, November 28, 11 Connections between Uniform Circular Motion and Simple Harmonic Motion An object in simple harmonic motion has the same motion as one component of an object in uniform circular motion: Monday, November 28, 11 Simple harmonic motion viewed as a projection If you illuminate uniform circular motion (say by shining a flashlight on a candle placed on a rotating lazy-Susan spice rack), the shadow projection that will be cast will be undergoing simple harmonic motion. Monday, November 28, 11 Connections between Uniform Circular Motion and Simple Harmonic Motion Here, the object in circular motion has an angular speed of 2π ω= T where T is the period of motion of the object in simple harmonic motion. Monday, November 28, 11 Connections between Uniform Circular Motion and Simple Harmonic Motion The position as a function of time: ⎛ 2π ⎞ x = A cosθ = A cos(ω t) = A cos ⎜ t⎟ ⎝ T ⎠ The angular frequency: Monday, November 28, 11 SHM phase, position, velocity, and acceleration SHM can occur with various phase angles. x = A cos(ω t + φ ) Monday, November 28, 11 For a given phase we can examine position, velocity, and acceleration. Connections between Uniform Circular Motion and Simple Harmonic Motion x = A cos(ω t) The velocity as a function of time: dx v= = −Aω sin(ω t) dt And the acceleration: 2 dv d x 2 a= = 2 = −Aω cos(ω t) dt dt Both of these are found by taking components of the circular motion quantities. Monday, November 28, 11 The Period of a Mass on a Spring The force on a mass on a spring is proportional to the displacement (Hooke’s law), and to the acceleration (Newton’s second law) F = ma = −kx since x = A cos(ω t) and a = −Aω cos(ω t) 2 m ⎡⎣ −Aω cos(ω t) ⎤⎦ = −k [ A cos(ω t)] 2 mω = k k 2 ω = m 2 ω= Monday, November 28, 11 k m As ω= k 2π = 2π f = m T So 1 f = 2π k m m T = 2π k Monday, November 28, 11 Frequency and Period The frequency of oscillation depends on physical properties of the oscillator; it does not depend on the amplitude of the oscillation. Monday, November 28, 11 The Period of a Mass on a Spring Therefore, the period is m T = 2π k Monday, November 28, 11 Characteristics of SHM Monday, November 28, 11 Characteristics of SHM Monday, November 28, 11 X versus t for SHO then simple variations on a theme Monday, November 28, 11 Energy in Simple Harmonic Motion As a mass on a spring goes through its cycle of oscillation, energy is transformed from potential to kinetic and back to potential. Monday, November 28, 11 Energy Conservation in Oscillatory Motion In an ideal system with no nonconservative forces, the total mechanical energy is conserved. For a mass on a spring: 1 1 E = K +U = mv + 2 2 2 kx 2 Since we know the position and velocity as functions of time, we can find the maximum kinetic and potential energies: U max 1 2 = kA , i.e. when x = A 2 As v = rω , and in this case rmax = A, and ω = K max k m 1 2 1 1 1 2 2 2 2 k = mv max = mA ω max = mA = kA 2 2 2 m 2 Monday, November 28, 11 Energy Conservation in Oscillatory Motion As a function of time, 1 2 1 2 E = K + U = mv + kx 2 2 2 2 2 2 v = −Aω sin(ω t) ⇒ v = A ω sin (ω t) x = A cos(ω t) ⇒ x = A cos (ω t) 2 So the total energy is constant; as the kinetic energy increases, the potential energy decreases, and vice versa. Monday, November 28, 11 ω= 2 2 k 2 ⇒ mω = k m 1 1 2 2 2 2 2 E = mA ω sin (ω t) + kA cos (ω t) 2 2 1 2 2 1 2 2 E = kA sin (ω t) + kA cos (ω t) 2 2 1 2 2 2 E = kA ⎡⎣sin (ω t) + cos (ω t) ⎤⎦ 2 Energy Conservation in Oscillatory Motion This diagram shows how the energy transforms from potential to kinetic and back, while the total energy remains the same. Monday, November 28, 11 Energy in SHM Monday, November 28, 11 Energy in SHM • Energy is conserved during SHM and the forms (potential and kinetic) interconvert as the position of the object in motion changes. Monday, November 28, 11 Monday, November 28, 11 The Pendulum A physical pendulum is a solid mass that oscillates around its center of mass. Examples: Monday, November 28, 11 The Pendulum A simple pendulum consists of a mass m (of negligible size) suspended by a string or rod of length L (and negligible mass). The angle it makes with the vertical varies with time as a sine or cosine. Monday, November 28, 11 The Pendulum Looking at the forces on the pendulum bob, we see that the restoring force is proportional to sin θ, whereas the restoring force for a spring is proportional to the displacement (which is θ in this case). Monday, November 28, 11 The Pendulum However, for small angles, sin θ and θ in radians are approximately equal. Monday, November 28, 11 The Pendulum However, for small angles, sin θ and θ in radians are approximately equal. Monday, November 28, 11 The Pendulum For small angles θ in radians is approximately the sine of θ, θ ≈ sin θ The net tangential force acting on m is the tangential component of its weight, and is always direct towards the equilibrium point F = mg sin θ ≈ mgθ The arc length displacement of the mass from equilibrium is s ⎛ mg ⎞ S = Lθ ⇒ θ = ⇒ F = mg sin θ ≈ mgθ = ⎜ s ⎟ ⎝ L ⎠ L For a spring F=kx We can use this same form for a pendulum if we let s=x, and k=mg/L m m L As T = 2π = 2π = 2π k mg L g So the period depends on the length of the pendulum and the acceleration due to gravity Monday, November 28, 11 Vibrations of molecules Two atoms separated by their internuclear distance r can be pondered as two balls on a spring. Monday, November 28, 11 Vibrations of molecules Two atoms separated by their internuclear distance r can be pondered as two balls on a spring. The potential energy of such a model is constructed many different ways. The Leonard–Jones potential is sketched below. The atoms on a molecule vibrate as shown below. Monday, November 28, 11 Damped Oscillations In most physical situations, there is a nonconservative force of some sort, which will tend to decrease the amplitude of the oscillation, and which is typically proportional to the speed: This causes the amplitude to decrease exponentially with time: Monday, November 28, 11 Damped Oscillations This exponential decrease is shown in the figure: Monday, November 28, 11 Damped Oscillations The previous image shows a system that is underdamped – it goes through multiple oscillations before coming to rest. A critically damped system is one that relaxes back to the equilibrium position without oscillating and in minimum time; an overdamped system will also not oscillate but is damped so heavily that it takes longer to reach equilibrium. Monday, November 28, 11 Damping Monday, November 28, 11 Damped oscillations A person may not wish for the object they study to remain in SHM. Consider shock absorbers and your automobile. Without damping the oscillation, hitting a pothole would set your car into SHM on the springs that support it. Monday, November 28, 11 Driven Oscillations and Resonance An oscillation can be driven by an oscillating driving force; the frequency of the driving force may or may not be the same as the natural frequency of the system. Monday, November 28, 11 A mass on a spring is driven by a large geared motor apparatus, and exhibits resonance at the appropriate frequency. Below resonance, the driving motion is in phase with the motion of the mass. At resonance the mass is 90 degrees out of phase with the driving motion, and above resonance it is 180 degrees out of phase. Note the amplitude of motion difference when the system is at resonance. Monday, November 28, 11 Resonance y = Ae t − τ The response curve becomes taller and narrower as damping is reduced Monday, November 28, 11 Driven Oscillations and Resonance If the driving frequency is close to the natural frequency, the amplitude can become quite large, especially if the damping is small. This is called resonance. Monday, November 28, 11 Forced (driven) oscillations and resonance • A force applied “in synch” with a motion already in progress will resonate and add energy to the oscillation • A singer can shatter a glass with a pure tone in tune with the natural “ring” of a thin wine glass. Monday, November 28, 11 Forced (driven) oscillations and resonance The Tacoma Narrows Bridge suffered spectacular structural failure after absorbing too much resonant energy Monday, November 28, 11 Summary • Period: time required for a motion to go through a complete cycle • Frequency: number of oscillations per unit time • Angular frequency: • Simple harmonic motion occurs when the restoring force is proportional to the displacement from equilibrium. Monday, November 28, 11 Summary • The amplitude is the maximum displacement from equilibrium. • Position as a function of time: ⎛ 2π ⎞ x = A cos ⎜ t ⎟ = A cos (ω t ) ⎝ T ⎠ • Velocity as a function of time: v = −Aω sin (ω t ) Monday, November 28, 11 Summary © 2010 Pearson Education, Inc. Monday, November 28, 11 Slide 14-32 Summary • Acceleration as a function of time: • Period of a mass on a spring: • Total energy in simple harmonic motion: Monday, November 28, 11 Summary • Potential energy as a function of time: • Kinetic energy as a function of time: • A simple pendulum with small amplitude exhibits simple harmonic motion Monday, November 28, 11 Summary • Period of a simple pendulum: • Period of a physical pendulum: Monday, November 28, 11 Summary © 2010 Pearson Education, Inc. Monday, November 28, 11 Slide 14-33 Summary • Oscillations where there is a nonconservative force are called damped. • Underdamped: the amplitude decreases exponentially with time: • Critically damped: no oscillations; system relaxes back to equilibrium in minimum time • Overdamped: also no oscillations, but slower than critical damping Monday, November 28, 11 Summary • An oscillating system may be driven by an external force • This force may replace energy lost to friction, or may cause the amplitude to increase greatly at resonance • Resonance occurs when the driving frequency is equal to the natural frequency of the system Monday, November 28, 11 Quiz 1. The type of function that describes simple harmonic motion is A. B. C. D. E. linear exponential quadratic sinusoidal inverse Monday, November 28, 11 Answer 1. The type of function that describes simple harmonic motion is A. B. C. D. E. linear exponential quadratic sinusoidal inverse Monday, November 28, 11 Quiz 2. A mass is bobbing up and down on a spring. If you increase the amplitude of the motion, how does this affect the time for one oscillation? A. The time increases. B. The time decreases. C. The time does not change. Monday, November 28, 11 Answer 2. A mass is bobbing up and down on a spring. If you increase the amplitude of the motion, how does this affect the time for one oscillation? A. The time increases. B. The time decreases. C. The time does not change. Monday, November 28, 11 Reading Quiz 3. If you drive an oscillator, it will have the largest amplitude if you drive it at its _______ frequency. A. special B. positive C. resonant D. damped E. pendulum Monday, November 28, 11 Answer 3. If you drive an oscillator, it will have the largest amplitude if you drive it at its _______ frequency. A. special B. positive C. resonant D. damped E. pendulum Monday, November 28, 11 Additional Questions Four 100 g masses are hung from four springs, each with unstretched length 10 cm. The four springs stretch as noted in the following diagram: Now, each of the masses is lifted a small distance, released, and allowed to oscillate. Rank the oscillation frequencies, from highest to lowest. A. a > b > c > d B. d > c > b > a C. a = b = c = d Monday, November 28, 11 Answer Four 100 g masses are hung from four springs, each with unstretched length 10 cm. The four springs stretch as noted in the following diagram: Now, each of the masses is lifted a small distance, released, and allowed to oscillate. Rank the oscillation frequencies, from highest to lowest. A. a > b > c > d B. d > c > b > a C. a = b = c = d Monday, November 28, 11 Increasing k increases f Additional Questions A typical earthquake produces vertical oscillations of the earth. Suppose a particular quake oscillates the ground at a frequency 0.15 Hz. As the earth moves up and down, what time elapses between the highest point of the motion and the lowest point? A. B. C. D. 1s 3.3 s 6.7 s 13 s Monday, November 28, 11 Answer A typical earthquake produces vertical oscillations of the earth. Suppose a particular quake oscillates the ground at a frequency 0.15 Hz. As the earth moves up and down, what time elapses between the highest point of the motion and the lowest point? A. B. C. D. 1s 3.3 s 6.7 s 13 s 1 1 1 T f = ⇒T = = = 6.67 ⇒ = 3.33 T f 0.15 2 Time between highest and lowest point is T/2 Monday, November 28, 11 Answer A typical earthquake produces vertical oscillations of the earth. Suppose a particular quake oscillates the ground at a frequency 0.15 Hz. As the earth moves up and down, what time elapses between the highest point of the motion and the lowest point? A. B. C. D. 1s 3.3 s 6.7 s 13 s 1 1 1 T f = ⇒T = = = 6.67 ⇒ = 3.33 T f 0.15 2 Time between highest and lowest point is T/2 Monday, November 28, 11 Q13.1 An object on the end of a spring is oscillating in simple harmonic motion. If the amplitude of oscillation is doubled, how does this affect the oscillation period T and the object’s maximum speed vmax? A. T and vmax both double. B. T remains the same and vmax doubles. C. T and vmax both remain the same. D. T doubles and vmax remains the same. E. T remains the same and vmax increases by a factor of Monday, November 28, 11 . A13.1 An object on the end of a spring is oscillating in simple harmonic motion. If the amplitude of oscillation is doubled, how does this affect the oscillation period T and the object’s maximum speed vmax? A. T and vmax both double. B. T remains the same and vmax doubles. C. T and vmax both remain the same. D. T doubles and vmax remains the same. E. T remains the same and vmax increases by a factor of Monday, November 28, 11 . Q13.2 This is an x-t graph for an object in simple harmonic motion. At which of the following times does the object have the most negative velocity vx? A. t = T/4 B. t = T/2 C. t = 3T/4 D. t = T Monday, November 28, 11 A13.2 This is an x-t graph for an object in simple harmonic motion. At which of the following times does the object have the most negative velocity vx? A. t = T/4 B. t = T/2 C. t = 3T/4 D. t = T Monday, November 28, 11 Q13.3 This is an x-t graph for an object in simple harmonic motion. At which of the following times does the object have the most negative acceleration ax? A. t = T/4 B. t = T/2 C. t = 3T/4 D. t = T Monday, November 28, 11 A13.3 This is an x-t graph for an object in simple harmonic motion. At which of the following times does the object have the most negative acceleration ax? A. t = T/4 B. t = T/2 C. t = 3T/4 D. t = T Monday, November 28, 11 Q13.4 This is an ax-t graph for an object in simple harmonic motion. At which of the following times does the object have the most negative displacement x? A. t = 0.10 s B. t = 0.15 s C. t = 0.20 s D. t = 0.25 s Monday, November 28, 11 A13.4 This is an ax-t graph for an object in simple harmonic motion. At which of the following times does the object have the most negative displacement x? A. t = 0.10 s B. t = 0.15 s C. t = 0.20 s D. t = 0.25 s Monday, November 28, 11 Q13.5 This is an ax-t graph for an object in simple harmonic motion. At which of the following times does the object have the most negative velocity vx? A. t = 0.10 s B. t = 0.15 s C. t = 0.20 s D. t = 0.25 s Monday, November 28, 11 A13.5 This is an ax-t graph for an object in simple harmonic motion. At which of the following times does the object have the most negative velocity vx? A. t = 0.10 s B. t = 0.15 s C. t = 0.20 s D. t = 0.25 s Monday, November 28, 11 Q13.6 This is an x-t graph for an object connected to a spring and moving in simple harmonic motion. At which of the following times is the potential energy of the spring the greatest? A. t = T/8 B. t = T/4 C. t = 3T/8 D. t = T/2 E. more than one of the above Monday, November 28, 11 A13.6 This is an x-t graph for an object connected to a spring and moving in simple harmonic motion. At which of the following times is the potential energy of the spring the greatest? A. t = T/8 B. t = T/4 C. t = 3T/8 D. t = T/2 E. more than one of the above Monday, November 28, 11 Q13.7 This is an x-t graph for an object connected to a spring and moving in simple harmonic motion. At which of the following times is the kinetic energy of the object the greatest? A. t = T/8 B. t = T/4 C. t = 3T/8 D. t = T/2 E. more than one of the above Monday, November 28, 11 A13.7 This is an x-t graph for an object connected to a spring and moving in simple harmonic motion. At which of the following times is the kinetic energy of the object the greatest? A. t = T/8 B. t = T/4 C. t = 3T/8 D. t = T/2 E. more than one of the above Monday, November 28, 11 Q13.8 To double the total energy of a mass-spring system oscillating in simple harmonic motion, the amplitude must increase by a factor of A. 4. B. C. 2. D. E. Monday, November 28, 11 A13.8 To double the total energy of a mass-spring system oscillating in simple harmonic motion, the amplitude must increase by a factor of A. 4. B. C. 2. D. E. Monday, November 28, 11 Q13.9 A simple pendulum consists of a point mass suspended by a massless, unstretchable string. If the mass is doubled while the length of the string remains the same, the period of the pendulum A. becomes 4 times greater. B. becomes twice as great. C. becomes greater by a factor of D. remains unchanged. E. decreases. Monday, November 28, 11 . A13.9 A simple pendulum consists of a point mass suspended by a massless, unstretchable string. If the mass is doubled while the length of the string remains the same, the period of the pendulum A. becomes 4 times greater. B. becomes twice as great. C. becomes greater by a factor of D. remains unchanged. E. decreases. Monday, November 28, 11 .