Download Linear Equations

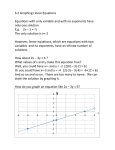
Linear Equations
Honors Advanced Algebra II with
Trigonometry
Ms. Lee
Essential Stuff
Essential Question
 How do you write the equation of linear
functions?
Essential Vocabulary




Linear Function
Slope-Intercept Form
Point-Slope Form
Standard Form
Linear Functions
 A linear function is a function whose
graph is a line.
 Linear equation: equation containing x
and/or y, where the exponent of both is 1.
 In a linear equation…
 Independent Variable is x
 Dependent Variable is y
Linear Equations
 To write a linear equation, you must
have two pieces of information…
 Point on the Line
 Slope of the Line
 Slope isn’t always given… may have
to use information to find it.
Slope of Lines
 Given points (x1,y1) and (x2,y2):
y2  y1
slope  m 
x2  x1
 Slope is 0 if 0 on top, and undefined is 0 is
on bottom.
 Slope = 0… Horizontal Line
 Slope = undefined… Vertical Line
Find the Slope
Find the slope of the line that passes
through the given points.
1. (-2,3), (5,1)
2. (8,5), (-2,-3)
3. (4,-6), (2,-6)
4. (-7,10), (1,-1)
5. (3,-5), (-8,-3)
6. (2,-5), (2,-8)
Linear Equations
 Point-Slope Form: y – y1 = m(x – x1)
 Point = (x1, y1)
and
slope = m
 Slope-Intercept Form: y = mx + b
 Slope = m
and
y-intercept = b
 Standard Form: Ax + By = C
 A, B, C = integers
and A is positive
Special Lines
 Horizontal Lines: y = constant
 Vertical Lines:
x = constant
 Parallel Lines: two lines with same slope
 Perpendicular Lines: two lines with slopes
that are opposite reciprocals
Homework
Homework 1.3