Download Print - Circulation Research

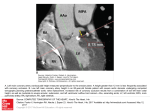
319
Profound Spatial Heterogeneity of
Coronary Reserve
Discordance Between Patterns of Resting and Maximal
Myocardial Blood Flow
Richard E. Austin Jr., Gabriel S. Aldea, Dwain L. Coggins,
Arthur E. Flynn, and Julien I.E. Hoffman
Downloaded from http://circres.ahajournals.org/ by guest on June 14, 2017
We examined the ability of individual regions of the canine left ventricle to increase blood flow
relative to baseline rates of perfusion. Regional coronary flow was measured by injecting
radioactive microspheres over 90 seconds in seven anesthetized mongrel dogs. Preliminary
experiments demonstrated a correlation between the regional distributions of blood flow during
asphyxia and pharmacological vasodilatation with adenosine (mean r=0.75; 192 regions in
each of two dogs), both of which resulted in increased coronary flow. Subsequent experiments,
during which coronary perfusion pressure was held constant at 80 mm Hg, examined the
pattern of blood flow in 384 regions (mean weight, 106 mg) of the left ventricular free wall
during resting flow and during maximal coronary flow effected by intracoronary adenosine
infusion. We found that resting and maximal flow patterns were completely uncorrelated to
each other in a given dog (mean r=0.06, p=NS; n=3 dogs). Furthermore, regional coronary
reserve, defined as the ratio of maximal to resting flow, ranged from 1.75 (i.e., resting flow was
57% of maximum) to 21.9 (resting flow was 4.5% of maximum). Thus, coronary reserve is
spatially heterogeneous and determined by two distinct perfusion patterns: the resting (control)
pattern and the maximal perfusion pattern. Normal hearts, therefore, contain small regions
that may be relatively more vulnerable to ischemia. This may explain the patchy nature of
infarction with hypoxia and at reduced perfusion pressures as well as the difficulty of using
global parameters to predict regional ischemia. Despite the wide dispersion of coronary reserve,
we found, by autocorrelation analysis, that reserve in neighboring regions (even when separated
by a distance of several tissue samples) was significantly correlated. This also applied to
patterns of resting myocardial flow. Thus, both resting coronary blood flow and reserve appear
to be locally continuous and may define functional zones of vascular control and vulnerability,
respectively. (Circulation Research 1990;67:319-331)
It is now well accepted that myocardial perfusion
is spatially heterogeneous. Not only is this lack
of uniformity apparent when one considers
blood flow to the heart by layer (i.e., a given depth
from the epicardial surface) but also when one
examines coronary flow to regions within a layer.1-8
Regional variability of perfusion, which has been
observed in the hearts of all species studied thus far,
From the Cardiovascular Research Institute and Departments
of Surgery, Pediatrics, and Cardiology, University of California,
San Francisco, Calif.
Supported in part by program project grant HL-25847 from the
National Institutes of Health. R.E.A. is a Stanley J. Sarnoff fellow;
G.S.A. and D.L.C. are supported by grant HL-07192 from the
National Institutes of Health; A.E.F. is supported by the American
Heart Association, California Affiliate.
Address for correspondence: Julien I.E. Hoffman, MD, Box
0544, University of California, San Francisco, CA 94143.
Received May 25, 1989; accepted March 13, 1990.
is quantitatively much larger than the error of the
techniques used to measure blood flow.9 King et al,3
for example, have found that even after correcting for
methodological error and temporal variability, flow
to small regions of the left ventricle of conscious
baboons ranges almost sixfold in its extremes.
Although the basis for such heterogeneity remains to
be explained, differences in local metabolic needs,
perhaps secondary to differences in regional function, have been suggested.2'3
Physiologically more interesting than resting differences in perfusion, however, is the ability of
individual regions to meet blood flow demands in
times of need (e.g., with exercise or decreased perfusion pressure). Studies of regional blood flow in the
absence of coronary tone demonstrate that the distribution of maximal flow - as with resting flow - is
extremely heterogeneous.6 This suggests that seem-
320
Circulation Research Vol 67, No 2, August 1990
Downloaded from http://circres.ahajournals.org/ by guest on June 14, 2017
ingly intrinsic properties, such as maximal regional
blood flow, vary significantly throughout the heart.
In this study, we examined the relative ability of
myocardial regions to increase blood flow by comparing resting and maximal flows in individual small
regions of the heart. We wondered whether regions
with higher than average resting flow also have
higher than average maximal flow. The correspondence between resting and maximal perfusion patterns determines the spatial distribution of coronary
reserve. Poor correlation between these patterns
would result in a wide range of regional reserve,
whereas a good match implies a fairly uniform ability
to increase flow.
To evaluate these possibilities, we studied the distribution of left main coronary artery (LMCA) blood flow
using separately labeled sets of radioactive microspheres to compare resting and maximal regional blood
flow at normal perfusion pressures. Initial experiments
addressed qualitative aspects of this comparison, as
well as the relation between pharmacological manipulation of vascular tone and the physiological challenge
of asphyxia. In the remaining experiments, coronary
perfusion pressure was held constant to allow absolute
comparisons of regional blood.
Materials and Methods
Experimental Preparation
We studied seven mongrel dogs of both sexes
weighing 23.9-29.5 kg. Each was sedated with
sodium thiopental (25 mg/kg i.v.) before endotracheal intubation and mechanical ventilation with
room air supplemented by oxygen at tidal volumes of
15-20 ml/kg. Anesthesia was maintained with 1%
halothane. Periodic arterial blood gas measurements
allowed us to adjust ventilatory settings to keep pH,
Po2, and Pco2 within normal limits.
Femoral arterial catheters were placed for blood
gas sampling, aortic pressure monitoring, and microsphere reference samples. After left thoracotomy via
the fifth intercostal space, the heart was suspended in
a pericardial cradle. In two dogs, catheters were
inserted into the left atrium via the left atrial appendage to inject microspheres and adenosine.
In the five remaining dogs, LMCA perfusion pressure was held constant with a pressurized femoralcoronary shunt under servo control. After anticoagulation with heparin (10,000 units i.v. and then 5,000
units hourly), a Gregg cannula, as described by
Sarnoff et al,10 was inserted through the left subclavian artery, placed just inside the left coronary
ostium, and secured with an external silk ligature
around the proximal LMCA. Pressure at the distal
tip of the cannula was digitally sampled at 20 Hz and
compared with a previously calibrated target pressure. This feedback was used to modulate the opening and closing of an air valve connecting a 250mm Hg pressure source to a sealed air-blood level in
the femoral-coronary circuit (Figure 1). The servo
FIGURE 1. Schematic diagram of the servo-controlled
femoral-coronary Gregg circuit10 used in experiments requiring
constant coronary perfusion pressure.
system ensured that mean coronary pressure was
maintained within 0.5% of target pressure.
Blood Flow Measurements With Radiolabeled
Microspheres
Regional coronary blood flow was measured using
the radioactive microsphere technique." Each dog
received either intracoronary or left atrial injections
of 3-10 million 15+1.5-Am diameter (mean+SD)
microspheres over 90 seconds. These spheres contained the gamma-emitting nuclides 153Gd, 57Co,
14mIn 51Cr, "'Sn, 85Sr, 95Nb, 54Mn, and 65Zn (3M, St.
Paul, Minn.; New England Nuclear, Boston, Mass.),
each corresponding to a particular coronary blood
flow determination. To prevent aggregation, the
spheres were suspended in saline with surfactant
(0.01% Tween 80). In the dogs receiving left atrial
injections, femoral blood was collected continuously
during and for 2 minutes after the end of the
injection. The timed femoral artery withdrawal provided us with a microsphere-containing reference
sample collected at a known flow rate. This allowed
us to calculate absolute blood flow in a tissue sample
using the following relation":
Qsample = Qreference -Csample
Creference
Austin et al Heterogeneity of Coronary Reserve
Base
*Pi
mid -,'
~
.ll
-.
,..I1
~I
m]
mi
m]
EL... 5
RI
ME
m
m
-1
m
L-1
m
i
---1
-1
5.
-
---------
.o
---
m
-
m
%.--
-
-1
m
3
3
m
0
m
59-M
JP
xs~.1384
Downloaded from http://circres.ahajournals.org/ by guest on June 14, 2017
Apex
FIGURE 2. Left ventricular;free wall cutting scheme for dogs
receiving intracoronary microsphere injections. Thefree wall of
each left ventnicle was trimmed, cut into subendocardial
(endo), middle (mid), and subepicardial (epi) layers, and
sectioned into a total of 384 pieces.
where Qsaple is blood flow in the sample, Qreference iS
the rate of reference flow, Csample is the radioactivity
of the tissue sample, and Creference is the radioactivity
of the reference sample.
Regional myocardial blood flow measurements
based on intracoronary microsphere injections were
referenced to total LMCA flow as determined with
an in-line electromagnetic flow transducer. The
above relation holds if Qreference=LMCA flow and
Creference=total activity of the heart.
After the final microsphere injection, each dog was
killed with a large dose of pentobarbital, and its heart
was removed. The left ventricular free wall was
trimmed into a square approximately 6 cm on a side,
fixed in formaldehyde, and subsequently cut into
subendocardial, middle, and subepicardial layers.
Each layer was further subdivided into 128 regions
(Figure 2) with a mean piece weight of 106+30 mg
(mean±+SD); in the dogs receiving left atrial microsphere injections, there were 3 x 64=192 regions
(mean weight, 142±+44 mg). The radioactivity of each
of these samples was measured with a gamma detector. In the dogs receiving intracoronary injections,
the remainder of the heart was homogenized and
counted so that total heart radioactivity could be
calculated. In all, there were a total of 6,912 measurements in 2,304 regions of seven hearts.
The radioactivity of each sample of myocardium
was determined using a NaI(Tl) detector (Tracor
Analytic, TM Analytic, Brandon, Fla.) and a multichannel pulse height analyzer (Norland Corp., Fort
Atkinson, Wis.), along with a NOVA-3 minicomputer
(Data General, Southboro, Mass.). Individual nuclide
activities were determined using the least-squares
method described by Baer et al.'2 All samples were
counted for 3 minutes. The measured activity of each
321
tissue sample was corrected for differences in geometric configuration by applying an empirically established relation (least-squares linear fit) between sample weight and the measurement of known activities."
All blood samples were the same height and were
counted using calibrations based on reference samples
placed on the bottom of sample vials. We estimated
the errors of counting inherent to the NaI(Tl) detector
by using the goodness of fit of nuclide separation to
approximate the variance in the determinations of the
activity of each individual nuclide.12
Experimental Protocol
The initial phase of the study focused on the
patterns of coronary perfusion during increased coronary flow due to intra-atrial adenosine administration (350 gg/kg/min) or asphyxia induced by disconnecting the respirator for 90 seconds. Control
measurements were obtained before and between
interventions in the two dogs studied in this part of
the protocol. In the first dog, asphyxia preceded
adenosine infusion. This order was reversed in the
second dog. In both dogs regional blood flow was
measured using left atrial injections of microspheres.
For the remainder of the study, coronary perfusion
pressure was maintained at a pressure of 80 mm Hg
during all conditions in all dogs. In five dogs, we
examined the resting pattern of myocardial perfusion. In three of these, regional blood flow was also
determined during maximal coronary vasodilatation
with intracoronary infusions of adenosine (20 jig/
kg/min). Maximal coronary vasodilatation was confirmed in these dogs by temporarily doubling the
infusion rate without evidence of a concomitant
increase in left coronary blood flow.
In some of the dogs, temporal variability of
regional blood flow and experimental error of the
microsphere technique were evaluated by using
sequential or simultaneous microsphere injections
containing different radionuclides.
Numerical Methods
Statistical comparisons of coefficients of variation
(the ratio of the standard deviation of a distribution
of measurements to its mean) were performed using
the technique of Lewontin, as described by Zar.13
Correlation coefficients (r) were calculated in a standard fashion and refer to a "simple" or Pearson
product-moment correlation coefficient.13 Statistical
comparisons of correlation coefficients were made
using standard techniques.13 Comparisons among
layers were made by two-way analysis of variance.13
To assess local continuity, we studied autocorrelations of flow and reserve within a layer with respect
to distance. The autocorrelations were calculated by
evaluating the correlation of flow (or reserve) in
myocardial regions a given distance apart, without
regard to direction (i.e., isotropically). Specifically,
we first estimated covariance for each distance (d)
using the following relation:
Circulation Research Vol 67, No 2, August 1990
322
TABLE 1. Assessing Components of Error in the Microsphere Technique
Dogs 3-7
Dogs 1 and 2
Relative error
Mean
Relative error
Mean
3.3%
624
1,103
4.0%
Number of spheres/region
0.6%
0.8%
25,457
14,069
Counts (3 min)
6.7%
517
605
12.9%
Separation error (cpm)
7.8%
...
13.5%
...
Mean combined
Dogs 1 and 2, dogs in initial phase of study with increased coronary flow due to intra-atrial adenosine administration
(350 ,ug/kg/min); dogs 3-7, dogs with coronary perfusion pressure maintained at 80 mm Hg.
1
V(d) =-*
nd
Downloaded from http://circres.ahajournals.org/ by guest on June 14, 2017
result of the discrete and, therefore, stochastic
nature of both microsphere entrapment and radioactive disintegrations. The following relation has been
shown to account for all of the variability in relative
measurements and the majority of variability in absolute blood flow measurements with radioactive
microspheres14:
RE'total = RE2counting + RE2spheres
where REtotal is the total relative error of a microsphere measurement, REwounting is the error of separation and radioactive counting, and REspheres is the
Poisson error associated with the number of spheres
in a sample. Traditionally, only the latter component,
REspheres, has been considered when estimating
error.15 In dogs requiring microsphere reference
samples, additional error must be included.14"16
Based on the above relation, a theoretical estimate14
of the mean error of coronary blood flow due to the
microsphere technique can be calculated for both parts
of the study (Table 1). Simultaneous injections of
separately labeled microspheres during some of the
[Qa-Q][Qb-Q]
all regions a,b
distance d apart
where V(d) is the covariance for distance d, nd is the
number of regions distance d apart, Q is mean flow
per layer, and Qa and Qb are flows in regions (a and b,
respectively) that are distance d apart. The correlation
function [r(d)] is the ratio of the spatial covariance to
the variance of flow within a layer [V(O)]; that is,
V(d)
r (d)V(O)
We estimated the significance (versus zero) of an
autocorrelation for a specific distance by comparing
each point to 2/\/,i7 this is a commonly employed
approximation to twice the standard deviation (personal communication, D.R. Brillinger, University of
California, Berkeley).
Assessment of the Microsphere Method
The errors in microsphere blood flow measurements have, in part, a statistical basis.14-17 This is a
During Adenosine Infusion
12-
r = 0.93
10-
D
1
8-
"O
6-
E
44
CD
2
E
z
/
2
#1
~~~~~~~~Dogl
4
6
8
10
FIGURE 3. Plots showing
12
85
Sr
o
0
During Control Conditions
empiric assessment of the microsphere technique using simulta-
85Sr
10,
neous injections. Microspheres
containing different isotopes
were injected during different
manipulations of coronary flow.
During Adenosine Infusion
0
a10
'E
8.
3
6.
c
4.
2.
Dog 02
u .-.
153
Gd
0
2
4
6
51
Cr
Regional Blood Flow (milgm/min)
8
10
Austin et al Heterogeneity of Coronary Reserve
323
TABLE 2. Hemodynamic Parameters in Dogs Receiving Left Atrial Injections
Control
Asphyxia
R
Order of
Q
(mm HgQ
PAO
Dog interventions (ml/min) (mm Hg) min. ml-l) (mlmin)
1
C As C Ad
48
134/95
1.98
192
2
C Ad C As
40
124/98
2.46
157
C, control; As, asphyxia; Ad, adenosine; Q, left main coronary artery
resistance (calculated using diastolic pressure).
Downloaded from http://circres.ahajournals.org/ by guest on June 14, 2017
coronary blood flow manipulations in the initial dogs
allowed us to evaluate the error of the microsphere
method empirically (Figure 3). Because of the lower
coronary concentrations of microspheres in heart tissue
with left atrial injections, blood flow determinations in
the initial dogs had significantly more error than in the
remaining dogs. It should be noted that examinations of
the variability of microsphere measurements of
regional blood flow only assess the reproducibility of
the technique and do not encompass systematic errors
of the microsphere technique.9
Results
Initial Regional Coronary Flow Measurements
Table 2 outlines the order of interventions, the
mean LMCA flow, and the aortic blood pressure in
the dogs receiving left atrial microsphere injections.
During intra-atrial adenosine administration, mean
blood pressure fell in both dogs but was increased
markedly after 90 seconds of asphyxia.
Figure 4 demonstrates the distribution of regional
coronary blood flow for these dogs. Although mean
LMCA flow was greater during asphyxia than during
o
.2
a
o
D
E
Z
50
40
30
20
10
04
b
80.
'
70
m 601
.
42
.
.
.
4
6
8
10
Constant Coronary Perfusion Pressure
To eliminate the effect of changes in aortic pressure on coronary pressure during manipulations,
coronary perfusion pressure was held constant at 80
mm Hg via a Gregg circuit.10 Direct access to the
coronary circulation also provided a way to adminis-
Control
F
0
80.
-h
42
4
701
Asphyxia
6
8
10
Asphyxia
60
cc
so
SO
o
40
40
30
D 30
z
10
0
L-
2
4
80
70
60
50
40
30
20
z
10
0
6
#
8
10
0
2
4
46
8
10
80*
Adenosine
Infusion
Adenosine
Infusion
70
60
so
40
30
E
2
4
46
.1..
8
10
10
Regional Coronary Blood Flow (mlIgmin)
R
Dog #2
80
70
60
50
40
30
20
10
Control
R
PAO
(mm Hg.
Q
(mm Hg.
PAO
(mm Hg) min * ml- ) (ml/min) (mm Hg) min. ml- l)
170/110
0.57
162
90/45
0.28
153/115
0.73
141
93/62
0.44
flow; PAO, aortic blood pressure; R, left main coronary artery
adenosine infusion, coronary vascular resistance,
defined as the ratio of diastolic aortic pressure to
mean coronary flow, was lower during adenosine
infusion (Table 2). Figure 5 depicts a comparison of
coronary flow in regions of the left ventricular free
wall during different experimental conditions: control versus control, adenosine versus asphyxia, and
adenosine versus control. The correlation was significant only when we compared either 1) regional flow
during adenosine administration to flow during
asphyxia or 2) repeat measurements of resting
regional flow (p<0.001). The distribution of coronary flow was poorly, or not significantly, correlated
when we compared resting regional flow (during
control conditions) with flow during either high coronary flow condition (i.e., asphyxia or adenosine).
Dog #1
80
70
60
Adenosine
~0
_
2
4
6
8
10
Regional Coronary Blood Flow (milg/min)
FIGURE 4. Histograms showing distribution of regional coronary flow during
different experimental conditions in dogs
receiving left atrial microsphere injections. Arrows indicate mean flow for
each condition.
324
Circulation Research Vol 67, No 2, August 1990
-4
c
8E 8.
0
CO
o 6.
c
3
0
0
2
0
E
Elo-
0)
'g0
.s 10-
c
CD
a
*0
c
p0
c
CD
c
@0
CJ1
c
1
2
3
Control Flow (mUlg/min)
4
4
r=0.75
_
0
2
4
6
8 10
Flow during Asphyxia (mllglmin)
c 8
0
*0
64
r=0.36
2
0
_
%
E
4'
c0
c
iL O.
E
CD
to6
0
4.
0
0
0.
0
m
0 2.
r=0.76
8.
00
0
-5
-E
c
E
'
0O;4-
81
4
-
1
2
3
Control Flow (ml/g/min)
1
4
00 ob00
to0 0
0
0
°t3
*0
b*:
0
Downloaded from http://circres.ahajournals.org/ by guest on June 14, 2017
'i4
0
0
0
rL
c
09
0
2
r=.7 ;4
!0.74
!0
0
1
2
3
Control Flow (mllglmin)
1
0.
p000
0
i
0
00
O0
10
*
0
@ 0
c
0
r=0.08
-
4
1
2
3
Control Flow (mulg/min)
of regional coronary flow during different experimental manipulations in dog 1 (top
4
0
2
4
6
8
Flow during Asphyxia (milg/min)
FIGURE 5. Plots showing comparisons
panels) and dog 2 (bottom panels). Not depicted are plots of asphyxia
1 and dog 2 of 0.38 and 0.21, respectively.
ter adenosine locally and, therefore, reduce total
systemic dose (intracoronary doses
intra-atrial doses).
were
1/17 of
Regional Distribution of Coronary Blood Flow
We assessed the distribution of regional blood flow
in five dogs with intracoronary microsphere injections. Figure 6 illustrates a typical distribution from a
single dog. This dog had a coefficient of variation of
regional flows of 17.6%. Although mean flow was
1.58 ml/g/min, the extremes of flow ranged more than
threefold. The mean coefficient of variation in all
dogs was 24.3% (n=5). We also examined regional
flow by layer and found no consistent pattern among
dogs (Table 3).
Using intracoronary infusions of adenosine, we
examined the regional pattern of coronary perfusion
versus
0
control, which had correlation coefficients in dog
in the absence of vascular tone. Figure 6 displays the
distribution of maximal regional flow from a single
dog. Although mean flow rose to 8.14 ml/g/min, the
distribution of regional flow ranged more than fourfold. The coefficient of variation was 33.1% in this
dog and averaged 30.4% for all three dogs (significantly different from the resting flow coefficient of
variation, p<O.05). When we assessed flow by layer
(Table 3), we found that maximal flow was significantly less in the subepicardial layer than in the inner
layers (p<0.05 by two-way analysis of variance).
Temporal Stability of Flow Distributions
The stability of these distributions was assessed by
injecting a second label 5 minutes after the first
(Figure 7). We found strong correlation between
repeat measurements of resting flow in dogs thus
45
0
c
0
FIGURE 6. Histograms showing distrbution of
regional coronary flow in a single dog receiving
intracoronary microsphere injections. Left panel:
Resting (control) distrbution. Right panel: Distribution of maximal regional flow for the same dog.
.a
0
Q)
0
0
.0
E
E
z
z
.5
1
1.5
2
2.5
Regional Control Flow (mulg/min)
0 2 4 6 8 10 12 14 16
Regional Flow during Adenosine (ml/g/min)
Austin et al Heterogeneity of Coronary Reserve
325
TABLE 3. Mean Regional Flow and Reserve by Ventricular Layer
Reserve
Maximum (ml/g/min)
Control (ml/g/min)
Epi
Mid
Endo
Epi
Mid
Endo
Epi
Endo
Mid
Dog
...
...
...
...
...
...
0.94
3
1.22
1.28
...
...
...
...
...
...
1.26
4
1.05
1.13
5.07
7.98
6.60
6.39
9.02
10.1
1.67
1.52
1.53
5
3.10
4.69
3.78
3.50
4.69
4.04
1.13
1.00
6
1.07
6.84
9.27
8.92
6.91
9.46
9.45
1.01
1.02
7
1.06
5.00*
6.95
6.63
5.60*
7.72
7.86
1.12
1.19
1.11
Mean
Reserve is maximum flow divided by control flow. Endo, subendocardium; mid, midwall; epi, subepicardium.
*Significantly different from the inner layers by two-way analysis of variance (p<0.05 andp<0.01 for maximum flow
and reserve, respectively).
Downloaded from http://circres.ahajournals.org/ by guest on June 14, 2017
flows of regions a given distance apart (Figure 10).
This provided a way to compare relative flows in
neighboring regions and to demonstrate that, although
regional flow (and reserve) may be highly variable
within a layer, it appears to be locally continuous since
flow correlation consistently increased at shorter and
shorter distances. One can assess the size of these
"zones of continuity" by estimating r1/2, the halfcorrelation distance (i.e., the distance at which the
autocorrelation falls to 0.5).18 For simplicity, we estimated r1/2 from the best-fit line predicted by the
least-squares method. The mean r1/2 for all layers
during control conditions was 3.5 mm (n = 15 layers in
five dogs). The mean r1/2 of the maximum flow patterns
was 8.4 mm, and the mean r1/2 of regional reserve was
7.6 mm (n =9 layers in three dogs). We noted that the
half-correlation distances for reserve were generally
longer in the subepicardium than in the subendocardium, suggesting greater continuity of regional reserve
in the outer layers of the heart (Figure 11). Figure 12,
a perspective plot from a single dog, graphically
depicts the increasing continuity of regional reserve in
the direction of the subepicardium.
Another way to assess local continuity is to note the
maximum distance at which there is significant autocorrelation. Although this parameter is more sensitive to
the errors of the microsphere technique (i.e., increased
methodological error would shorten the maximum distance of correlation), it sets a minimum on the range
over which flow in two regions is correlated. The mean
maximum distance of significant correlation was
9.2±3.1 mm for resting flow (n=15 layers). It was
12.0+4.4 and 11.4+3.5 mm for maximum flow and
regional reserve, respectively (n=9 layers).
studied (mean r=0.93, n=3). In other words, regions
that tended to have low flows continued, over time, to
have low flows, and regions with higher than average
blood flow remained high. The patterns of blood flow
during maximal coronary vasodilatation were also
found to be very stable over time (Figure 7).
Regional Coronary Reserve
Because resting and maximal regional blood flow
displayed heterogeneous distributions, we compared
flow in each region during resting flow with the
region's blood flow during pharmacological coronary
vasodilatation. Figure 8 demonstrates the lack of
correlation between resting and maximal flow patterns in all dogs examined (mean r=0.06, p=NS).
Pieces with high resting flow, therefore, had no
greater tendency to have above-average maximal flow
than pieces with low resting flow.
Figure 9 contains histograms of the distribution of
regional coronary flow reserve for these dogs. We
defined reserve as the ratio of maximum flow to resting
flow at a given perfusion pressure. Note that although
the mean reserve in these dogs was 6.2, it ranged from
1.75 (i.e., resting flow was 57% of maximum) to 21.9
(resting flow was 4.5% of maximum). In addition,
distributions were skewed to the right, suggesting a
physiological lower limit for coronary reserve.
Continuity of Flow and Flow Reserve Pattems
Finally, we examined the degree of local continuity
of flow and flow reserve using autocorrelation, that is,
by comparing all possible pairings of pieces within a
layer (there were 8,128 such comparisons per layer per
dog) and calculating the mean correlation among
E
FIGURE 7. Plots evaluating the temporal stability
of the distribution of regional blood flow. A second
set of microspheres containing a different nuclide
was injected 5 minutes after the first. Left panel:
Comparison of repeated measurements of regional
controlflow. Right panel: Comparison of repeated
measurements of maximal regionalflow. (This dog
is also depicted in Figure 6).
E
r = 0.91
E2
3.1CD
0
40
o
-a
CD
0
U.
0
1
a
0
0
i
/~~~~~
2= 0
i 2
Control Flow (mulg/min)
3
4
8
12
16
Regional Flow during Adenosine (mulg/min)
Circulation Research Vol 67, No 2, August 1990
326
o
0
7-
o
6-
*0
5
16-
._
CA
14-
(D
12
0
c
_
-
*
CD
Cu
.C
10-
0
_
.~ ^ 4-
190
BE8-
CP0
00
-6
E
0
0
*1
cc
O
0
r
*0
.5
r = 0.04
2
=
r
0.0
~
-t)
3
2
1
14
O
12
11
0.03
0
0
0
10
4
0
=
1
2
Regional Control Flow (ml/g/min).
Regional Control Flow (milg/min)
)
r
1
1a
FIGURE 8. Plots comparing regional
blood flow at rest with regional flow
during maximal pharmacological
vasodilatation with adenosine in three
dogs. (The dog depicted on the upper
left is in Figures 6 and 7.)
D00
10
o0
cc
00O
Downloaded from http://circres.ahajournals.org/ by guest on June 14, 2017
E
.g4 6
%,0CDE 4
B,
.2
2
cc
0
o
o
r
1
0
=
0.11
2
3
Regional Control Flow (milg/min)
We also analyzed the local correlation of resting
flow and reserve in the radial direction (i.e., layer
versus layer). We compared regional flow and reserve
in corresponding regions in the subendocardial, middle, and subepicardial layers. Mean correlation (r)
between adjacent layers was 0.63 and 0.67 for resting
flow and reserve, respectively (p<0.001). Mean correlation of flow and reserve between corresponding
601
20
45.
40
35,
cc 30
0
25
20
15
10
z
Dog #5
[skewness = .566]
50
c
0
U)
20
40
c
30
4)
0
E
z
E 10'
0 1.1
0
L
2
I
4
6
IA
8
10
5'
12
Regional Reserve (Maximal Flow/Control Flow)
60
50
CD
c
40
cc
30
20
E
z
Discussion
Critique of Method
As our assessment of regional flow is based solely
on microsphere measurements, the validity of this
Dog #6
(skewness = .245)
I
..
.-.Fr
X
,,- m ,
6
7
4
5
1
2
3
U0
Regional Reserve (Maximal Flow/Control Flow)
nj
4.a
L.*
pieces in the subendocardium and subepicardium
0.42 and 0.48, respectively (p<0.01).
was
10
25
15
20
10
5
g
Regional Reserve (Maximal Flow/Control Flow)
FIGURE 9. Histograms showing distribution of coronary reserve in three dogs at a
perfusion pressure of 80 mm Hg. Coronary
reserve is defined as the ratio of maximal
regional blood flow to control flow. Note
the consistent rightward skew.
Austin et al Heterogeneity of Coronary Reserve
Dog #3
20-1
Dog #7
*
1.0 r
1.0
inner Layer
Inner Layer
4
I
x-
8
12
\O0
E
0
16
1.0
0.0
0
4
8
12
16
Middle Layer
0
I
Dog #5
r 0.50
0
r 0.5
0
4
8
12
16
0.0
0
4
0
8
12
16
Downloaded from http://circres.ahajournals.org/ by guest on June 14, 2017
1.0
1.0 r
Outer Layer
Outer Layer
N\b
r o.
r 0.5[
'0"~
o.
i
4
middle
outer
j~/
,
1.0
Middle Layer
0
B
O
10*
!Q,
r112
0.0
inner
r on5
r 0.5 r- ---0
0
327
8
12
16
0
4
8
12
..
Dog #6
Dog #7
FIGURE 11. Bar graph showing half-correlation distance
(rj12) by layer for regional coronary reserve in three dogs. r1/2 is
the estimated distance (by least-squares method) at which
regional flow has a mean autocorrelation of 0.5. The mean
subepicardial r112 was significantly longer than in the inner
layers (p<O.OS by two-way analysis of variance). Because an
autocorrelation must equal one at a distance of zero (a point
we did not use in our regression), it is likely that, in general,
regional flow autocorrelations are not linearly related to
distance. Note that at times, we calculated the value for r1/2 by
extrapolating the best-fit line (Figure 10). Thus, some of our
estimates of r112 are conservative (i.e., perhaps shorter than true
16
Distance (mm)
FIGURE 10. Plots comparing mean autocorrelation of
regional flow versus distance in the subendocardial, middle,
and subepicardial layers of two dogs. Only significant autocorrelations have been plotted (see "Materials and Methods"). For
the inner layer of dog 3, the half-correlation distance (r112) has
been indicated (see also Figure 11). r, correlation coefficient.
Distance (mm)
technique is of primary importance in the interpretation of our results. The accuracy of the radioactive
microsphere technique has been examined extensively,7-9"11'15'16 and recently our laboratory has also studied this question in detail.14 There are two major
concerns with the microsphere technique: the degree
to which flow is proportional to sphere deposition and
the effect of microspheres on the microcirculation.
We evaluated the reproducibility of measurements
with microspheres both theoretically (Table 2) and
empirically (Figure 3), using simultaneous injections
of microspheres containing different isotopes. These
estimates of the error in flow (i.e., the stochastic
errors14) were minimal when compared with measured regional heterogeneity. Another potential
source of error with the microsphere technique is the
possibility that the rheological properties of the
spheres may prevent them from reflecting true blood
flow.8'9 Although large microspheres (e.g., 50 ,um in
diameter) have been demonstrated to deposit preferentially in areas of high flow,7-9 this appears to be
less important with smaller spheres such as the
15-,m spheres used in this study. Fifteen-micron
spheres have been shown to correlate well with
nonparticulate tracers, including iododesmethylimipramine.8'9 Thus, although it is likely that there
are significant systematic, as well as random, errors
associated with the microsphere technique, they
appear to be much smaller than the observed heterogeneity of flow and flow reserve we have found in
this study. Therefore, it is unlikely that our findings
are qualitatively affected by these errors.
Another concern with the microsphere technique
has been the degree of circulatory impairment after a
microsphere measurement. Surprisingly, even with
large numbers of spheres, the amount of microvasculature at risk with most measurements is small. In
our study, dogs that had four coronary microsphere
injections received a total of approximately 20 million
microspheres. We estimate this number of spheres to
affect only about 4% of capillaries.8 The apparent
temporal stability of repeat measurements of
regional flow (Figures 5 and 7) also suggests that
progressive circulatory impairment was minimal.
Another consideration is that our system of perfusing the LMCA may have resulted in a heretofore
unappreciated effect on measured heterogeneity.
Data from the initial dogs, which agrees qualitatively
with those from dogs in which the LMCA was
cannulated, suggest that our findings were not due to
an artifact associated with experimental control of
coronary perfusion. Finally, it is possible that the use
of anesthetized, open-chest dogs affected our measurements of flow and regional reserve. Previous
studies2,3,5-9"19 in conscious and anesthetized ani-
Circulation Research Vol 67, No 2, August 1990
328
r 1X2
=
2.82 mm
CV = 26.2%
Subendocardium
r 12 = 10.7 mm
CV=32A%
Midwall
mals, though, have demonstrated similar magnitudes
of flow heterogeneity. The effect of volatile anesthesia on regional flow in the absence of coronary tone
has been less well studied.
Downloaded from http://circres.ahajournals.org/ by guest on June 14, 2017
Regional Coronary Flow and Reserve
In our study we examined the regional distribution
of LMCA perfusion in the dog, specifically, the
pattern of blood supply to the left ventricular free
wall. We focused on the left ventricular free wall
because of its exclusive LMCA supply. In the initial
experiments we attempted to assess, primarily in a
qualitative way, the regional distribution of blood
flow during baseline conditions and two fundamentally different manipulations, both of which resulted
in marked increases in total coronary flow. Because
the number of microspheres per tissue sample was
limited in the dogs with left atrial microsphere
administration, there was a moderate amount of
error (Table 1). In addition, the opposing systemic
effects of these manipulations on aortic, and thus
coronary, perfusion pressure prevented absolute
comparisons of regional blood flow during different
experimental conditions. Nevertheless, comparisons
of relative regional flow provided several interesting
observations, some of which are corroborated by
findings in the latter part of this study.
First, although total LMCA flow varied with time,
the relative distribution of resting regional flow was
stable, even when compared before and several minutes after an experimental manipulation (Figure 5).
Second, there were strong correlations between patterns of regional perfusion when coronary flow was
increased, although the methods used to increase
coronary flow were quite different and actually had
opposite effects on arterial blood pressure (Table 2).
This is of interest because several laboratories have
recently demonstrated that, even during significant
reductions in coronary flow, vasodilatory reserve is
not exhausted.20,21 Our experiments demonstrate
that although the absolute change in regional vascular resistance during adenosine administration was
larger than with asphyxia, the relative change in a
given region was approximately the same. This suggests that the pharmacological recruitment of reserve
qualitatively, if not quantitatively, mimics the physi-
r12 = l5Amm CV = 25.2%
FIGURE 12. Perspective plots of
regional coronary reserve in
subepicardium, midwall and subendocardium for the dog depicted
in Figures 6-9. The coronary
reserve in each region is represented by the apparent height of
each intersection of lines r112,
half-correlation distance; CV,
coefficient of variation.
Subepicordium
ological response to increased blood flow demand
during hypoxia and hypercapnia.
Finally, there was little correlation between perfusion patterns when comparing relative regional flow
at rest and during increased coronary flow. It is
important to note that in the preliminary experiments we did not directly measure coronary flow and,
since our experimental manipulations were limited
by their systemic effects, we did not test whether
coronary flow was maximal.
To overcome these limitations, we controlled coronary blood flow in the remainder of the experiments
by means of a Gregg circuit.'0 This had several
advantages, the most important of which was control
of LMCA perfusion pressure. Because in the absence
of coronary autoregulation regional blood flow
depends on perfusion pressure, accurate comparisons of regional flow require constant coronary pressure. In addition, direct access to the coronary circulation enabled us to use doses of adenosine that
minimized systemic effects and thus to avoid significant changes in afterload that had been observed to
alter transmural distribution of regional blood flow.22
Direct access also ensured that the number of microspheres trapped by the myocardium would be independent of the type of experimental manipulation
and its effect on the distribution of cardiac output.
As in the initial dogs, we found significant spatial
heterogeneity of both baseline and maximum
regional flow. This agrees with several previous
studies.'-9"19 In addition, these distributions of flow
were found to be relatively constant over time (Figure 7). Studies in conscious animals3,5 demonstrate
that regional perfusion patterns can be quite stable
over several hours. Despite the stability of each flow
distribution, however, there was no correlation
between resting and maximal regional flow patterns
(Figure 8). Thus two distinct perfusion patterns
determine coronary flow reserve: the resting (or
control) pattern and the maximal flow pattern.
The resting distribution of regional myocardial
blood flow is of particular interest, because there is
evidence that under most conditions regional perfusion closely reflects local metabolic needs. First, it is
well known that the resting coronary arteriovenous
oxygen difference is near maximal (approximately
Austin et al Heterogeneity of Coronary Reserve
Downloaded from http://circres.ahajournals.org/ by guest on June 14, 2017
60-70%) and does not appreciably widen with exercise or reductions in coronary flow.23'24 This suggests
that myocardial blood supply and demand are optimally matched because little oxygen, even at rest,
passes unextracted through the myocardium. Second,
changes in regional contractility following changes in
coronary blood flow also suggest that regional perfusion is coupled to metabolic demand.25-27 Finally, the
increased myocardial oxygen requirement during
high coronary flow, a phenomenon known as the
Gregg effect,28 also provides an "incentive" for tight
control of coronary flow. These points suggest that
the heterogeneous distribution of regional coronary
flow probably reflects an equally heterogeneous metabolic demand.
The distribution of maximal regional blood flow,
on the other hand, appears to reflect factors that are
largely mechanical and quite separate from those
that influence regional perfusion when vascular tone
is intact. Coronary driving pressure, length of diastole, and extraluminal tissue pressure are major
determinants of maximum regional flow.29 Ultimately
though, the underlying vascular architecture establishes the upper limit of the maximum blood flow
possible to a given region of myocardium. Studies of
the regional vascularity of the heart reveal arteriolar
and capillary networks that have random branching
patterns.30,31 Indeed, recent models of regional blood
flow now incorporate the stochastic nature of the
vascular tree.32,33 Thus, a combination of factors
influences regional flow in the absence of vascular
tone and results in the spatially heterogeneous maximal perfusion pattern found in this and previous
studies.6 Because resting and maximal regional blood
flow patterns appear to be determined by distinct
factors, there is little reason to expect them to be
related.
The apparent mismatch between perfusion patterns has several implications. First, it implies there
are markedly different amounts of reserve from one
region to another. In this study, we had tissue samples with resting blood flows as low as 4.5%, and as
high as 57%, of maximal blood flow in the region
(Figures 8 and 9). Thus, especially when one considers that in humans mean coronary blood flow can
increase more than fourfold during heavy exercise,24,34 some regions required resting rates of perfusion that were relatively close to maximal capacity.
Extreme spatial heterogeneity of reserve may
explain the patchy nature of myocardial infarction
after hypoxia or global reductions in coronary perfusion pressure, for example, with cardiac tamponade,
shock, aortic valvular stenosis, or severe coronary
stenosis.35 Regions with low coronary flow reserve
simply may be more vulnerable. Studies using an
ultraviolet fluorescence technique to measure
reduced nicotinamide adenine dinucleotide have
demonstrated small regions of ischemia on the epicardial surface of perfused rat hearts either with low
perfusion pressure or during hypoxia.36,37 This suggests that the supply of oxygen can become locally
329
insufficient. Other tissues, for the same reasons, may
contain multiple foci of vulnerability. After decreases
in renal perfusion, for instance, ischemic damage to
the kidney is often patchy.38
Although the distribution of regional reserve may
explain the focal nature of infarction in the setting of
reduced perfusion pressure, it does not explain the
frequently subendocardial distribution of these
patchy infarcts. In fact, when we examined reserve by
layer, we found slightly less reserve at 80 mm Hg in
the subepicardium than in the middle and inner
layers (Table 3). Several investigators27'39 have demonstrated, however, that as coronary perfusion pressure is lowered, mean reserve falls more rapidly in
the inner layers. Thus, other factors, such as transmural tissue pressure or perhaps the movement of
blood flow from inner to outer layers during
systole,40-43 may significantly compromise subendocardial reserve at low perfusion pressures. Our
study suggests, though, that even when global factors
(e.g., elevated diastolic ventricular pressure or
reduced perfusion pressure) place the subendocardium at risk for ischemia, there will be islands of
relatively greater vulnerability within the inner layers
of the heart.
The spatial heterogeneity of reserve may also
explain the difficulty in predicting regional ischemia
using global measurements that do not take into
account the wide distribution of regional reserve. For
instance, it may be that some patients with symptoms
of stress-induced angina despite normal coronary
anatomy (as assessed by angiography)44'45 have
regionally inadequate coronary reserve. Conversely,
regional variability of reserve may make it misleading
to extrapolate about the heart as a whole using a
limited number of regional measurements46 (e.g.,
biopsies and regional pH measurements). In this
study, we found that, on average, measurements of
regional reserve were completely unrelated (i.e., not
significantly correlated) at distances greater than 11.4
mm. Thus, it may be wise to use several spatially
distinct samples in regional assessments of ischemia.
Our method of regional flow analysis allowed us to
examine a final consideration: the local continuity of
regional perfusion and reserve within layers of the
heart. This issue is separate from the assessment of
regional blood flow dispersion (e.g., the coefficient of
variation), which does not take into account the
degree of local variation among neighboring regions.
For example, when a layer of myocardium has
greater blood flow in the apex than the base, it
necessarily has a dispersion about the mean flow of
the layer. If, in the same layer, regional flow gradually,
but steadily, changed from apex to base, total dispersion could remain high while local discontinuity
(reflecting only the change from piece to piece in the
direction of the base-apex axis) would be minimal. In
fact, we had several instances in which the coefficient
of variation of regional flow increased or stayed the
same from one layer to the next, yet local discontinuity
fell (i.e., half-correlation distance, r,12, increased; Fig-
330
Circulation Research Vol 67, No 2, August 1990
Downloaded from http://circres.ahajournals.org/ by guest on June 14, 2017
ure 12). Of note, in all dogs in which we measured
reserve, we consistently found smaller half-correlation
distances in the inner layers, implying that regional
reserve was less continuous in the subendocardium
and midwall than in the subepicardium (Figures 11
and 12). In all dogs, we observed significant correlation of flow among neighboring regions of a layer. The
correlation was often significant over a distance of
several regions and consistently improved at shorter
distances (Figure 11). Bassingthwaighte et a119 have
recently proposed a fractal model of regional coronary
flow that predicts a moderately strong correlation
between local flows. In the current study, we have
used autocorrelation to directly demonstrate the
degree of local flow continuity.
Because flow in adjacent myocardial regions is correlated, these areas may be considered to be contained
within a functional zone ofvascular control. Using r112 as
a conservative estimate of the radius of such a zone, we
calculate a mean size of 0.38 cm2. Such a unit encompasses several hundred arterioles.47,48 Similarly, when
examining regional reserve, the r1/2 defines a "zone of
vulnerability," which, in our study, had a mean size in
the dog of approximately 1.8 cm2. Because reserve
appeared to be less continuous in the subendocardium
than the subepicardium, functional areas of reserve are
probably smaller in inner layers of the heart. The
mechanisms contributing to continuity of flow or flow
reserve in regions much larger than the area perfused
by a single arteriole-the major locus of control of
vascular resistance49-are unknown. Perhaps macroscopic factors, such as intraventricular or transmural
pressure, affect the caliber of vessels in a stochastic
microvasculature (and thus the maximal perfusion pattern) and influence local metabolic needs (and thus the
resting perfusion pattern) in a continuous way.
Acknowledgments
We would like to express our gratitude to Waleed
Husseini, Bruce Payne, and Carl McWatters for their
invaluable assistance with this project. We would also
like to express our debt to Dr. David Brillinger of the
Department of Statistics of the University of California
at Berkeley, who generously assisted in our analysis of
local continuity and provided the perspective plots.
References
1. Aldea GS, Austin RE Jr, Flynn AE, Coggins DL, Hoffman
2.
3.
4.
5.
JIE: The heterogeneous delivery of cardioplegic solution in
the nonischemic heart. J Thorac Cardiovasc Surg 1990;
99:345-353
Franzen D, Conway RS, Zhang H, Sonnenblick EH, Eng C:
Spatial heterogeneity of local blood flow and metabolite
content in dog hearts. Am J Physiol 1988;254:H344-H353
King RB, Bassingthwaighte JB, Hales JRS, Rowell LB: Stability of heterogeneity of myocardial blood flow in normal
awake baboons. Circ Res 1985;57:285-295
Kirk ES, Honig CR: Nonuniform distribution of blood flow
and gradients of oxygen tension within the heart. Am J Physiol
1964;207:661-668
Marcus ML, Kerber RE, Ehrhardt JE, Falsetti HL, Davis DM,
Abboud FM: Spatial and temporal heterogeneity of left ventricular perfusion in awake dogs. Am Heart J 1977;94:748-754
6. Sestier FJ, Mildenberger RR, Klassen GA: Role of autoregulation in spatial and temporal perfusion heterogeneity of
canine myocardium. Am J Physiol 1978;235:H64-H71
7. Utley J, Carlson EL, Hoffman JIE, Martinez HM, Buckberg
GD: Total and regional myocardial blood flow measurements
with 25,, 15,u, 9,u, and filtered 1-10Al diameter microspheres
and antipyrine in dogs and sheep. Circ Res 1974;34:391-405
8. Yipintsoi T, Dobbs WA Jr, Scanlon JD, Knopp TJ, Bassingthwaighte JB: Regional distribution of diffusible tracers and
carbonized microspheres in the left ventricle of isolated dog
hearts. Circ Res 1973;33:573-587
9. Bassingthwaighte JB, Malone MA, Moffett TC, King RB,
Little SE, Link JM, Krohn KA: Validity of microsphere
depositions for regional myocardial flows. Am J Physiol 1987;
253(Heart Circ Physiol 22):H184-H193
10. Sarnoff SJ, Case RB, Waithe PE, Isaacs JP: Insufficient
coronary flow and myocardial failure as a complicating factor
in late hemorrhagic shock. Am J Physiol 1954;176:439-444
11. Heymann MA, Payne BD, Hoffman JIE, Rudolph AM: Blood
flow measurements with radionuclide-labeled particles. Prog
Cardiovasc Dis 1977;20:55-79
12. Baer RW, Payne BD, Verrier ED, Vlahakes GJ, Molodowitch
D, Uhlig PN, Hoffman JIE: Increased number of myocardial
blood flow measurements with radionuclide-labeled microspheres. Am J Physiol 1984;246(Heart Circ Physiol 15):
H418-H434
13. Zar JH: Biostatistical Analysis. Englewood Cliffs, NJ, PrenticeHall, Inc, 1984, pp 122-125
14. Austin RE Jr, Hauck WW, Aldea GS, Flynn AE, Coggins DL,
Hoffman JIE: Quantitating error in blood flow measurements
with radioactive microspheres. Am J Physiol 1989;257(Heart
Circ Physiol 26):H280-H288
15. Buckberg GD, Luck JC, Payne DB, Hoffman JIE, Archie JP,
Fixler DE: Some sources of error in measuring regional blood
flow with radioactive microspheres. J Appl Physiol 1971;
31:598-604
16. Dole WP, Jackson DL, Rosenblatt JI, Thompson WL: Relative error and variability in blood flow measurements with
radiolabeled microspheres. Am J Physiol 1982;243(Heart Circ
Physiol 12):H371-H378
17. Nose Y, Nakamura T, Nakamura M: The microsphere method
facilitates statistical assessment of regional blood flow. Basic
Res Cardiol 1985;80:417-429
18. Bras RL, Rodriguez-Iturbe I: Random Functions and Hydrology. Reading, Mass, Addison-Wesley, 1985, p 335
19. Bassingthwaighte JB, King RB, Roger SA: Fractal nature of
regional myocardial blood flow heterogeneity. Circ Res 1989;
65:578-590
20. Aversano T, Becker L: Persistence of coronary vasodilator
reserve despite functionally significant flow reduction. Am J
Physiol 1985;248(Heart Circ Physiol 17):H403-H411
21. Grattan MT, Hanley FL, Stevens MB, Hoffman JIE: Transmural coronary reserve patterns in dogs. Am J Physiol 1986;
250(Heart Circ Physiol 19):H276-H383
22. Stevens MB, Hill AC, Mori H, Husseini W, Hoffman JIE: The
effect of wall forces on coronary flow, in Sideman S, Beyar R
(eds): Activation, Metabolism, and Perfusion of the Heart.
Dordrecht, The Netherlands, Martinus Nijhoff Publishing,
1987, pp 433-439
23. Feigl EO: Coronary Physiology. Physiol Rev 1983;63:1-205
24. Holmberg S, Serzysko W, Varnauskas E: Coronary circulation
during heavy exercise in control subjects and patients with
coronary heart disease. Acta Med Scand 1971;190:465-480
25. Canty JM Jr: Coronary pressure-function and steady-state
pressure-flow relations in the unanesthetized dog. Circ Res
1988;63:821-836
26. Downey JM: Myocardial contractile force as a function of
coronary blood flow. Am J Physiol 1976;230:1-6
27. Gallagher KP, Matsuzaki M, Koziol JA, Kemper WS, Ross J
Jr: Regional myocardial perfusion and wall thickening during
ischemia in conscious dogs. Am JPhysiol 1984;247:H727-H738
28. Gregg DE: Effect of coronary perfusion pressure or coronary
flow on oxygen usage of the myocardium. Circ Res 1963;
13:497-500
Austin et al Heterogeneity of Coronary Reserve
Downloaded from http://circres.ahajournals.org/ by guest on June 14, 2017
29. Raff WK, Kosche F, Lochner W: Extravascular coronary
resistance and its relation to microcirculation. Am J Cardiol
1972;29:598-603
30. Bassingthwaighte JB, Yipintsoi T, Harvey RB: Microvasculature of the dog left ventricular myocardium. Microvasc Res
1974;7:229-249
31. Grayson J, Davison JW, Fitzgerald-Finch A, Scott C: The
functional morphology of the coronary microcirculation in the
dog. Microvasc Res 1974;8:20-43
32. Dawant B, Levin M, Popel AS: Effect of dispersion of vessel
diameters and lengths in stochastic networks. Microvasc Res
1986;31:203-222
33. Wieringa PA, Spaan JAE, Stassen HG, Laird JD: Heterogeneous flow distribution in a three dimensional network simulation of the myocardial microcirculation. Microcirculation
1982;2:195-216
34. Kitamura K, Jorgensen CR, Gobel FL, Taylor HL, Wang Y:
Hemodynamic correlates of myocardial oxygen consumption
during upright exercise. JAppl Physiol 1972;32:516-522
35. Melcher GW, Walcott WW: Myocardial changes following
shock. Am J Physiol 1951;164:832-836
36. Barlow CH, Chance B: Ischemic areas in perfused rat hearts:
Measurement by NADH fluorescence photography. Science
1976;193:909-910
37. Steenbergen C, Deleeuw G, Barlow CH, Chance B, Williamson JR: Heterogeneity of the hypoxic state in the perfused rat
heart. Circ Res 1977;41:606-615
38. Brezis M, Rosen S, Silva P, Epstein FH: Renal ischemia: A
new perspective. Kidney Int 1984;26:375-383
39. Guyton RA, McClenathan JH, Newman GE, Michaelis LL:
Significance of subendocardial S-T segment elevation caused
by coronary stenosis in the dog. Am J Cardiol 1977;40:373-380
40. Arts T, Reneman RS: Interaction between intramyocardial
pressure (IMP) and myocardial circulation. J Biomech Eng
1985;107:51-56
331
41. Flynn AE, Coggins DL, Aldea GS, Austin RE Jr, Goto M,
Husseini W, Hoffman JIE: Ventricular contraction increases
subepicardial blood flow: Evidence for a deep myocardial
pump (abstract). FASEB J 1989;3:A1305
42. Hoffman JIE, Baer RW, Hanley FL, Messina LM, Grattan
MT: Regulation of transmural myocardial blood flow. J Biochem Eng 1985;107:2-9
43. Spaan JAE, Breuls NPW, Laird JD: Diastolic-systolic coronary flow differences are caused by intramyocardial pump
action in the anesthetized dog. Circ Res 1981;49:584-593
44. Likoff W, Segal BL, Kasparian H: Paradox of normal selective
coronary arteriograms in patients considered to have unmistakable coronary heart disease. N Engl J Med 1967;
276:1063-1066
45. Opherk D, Zebe H, Weihe E, Mall AG, Durr Ch, Gravert B,
Mehmel HC, Schwarz F, Kubler W: Reduced coronary dilatory capacity and ultrastructural changes of the myocardium in
patients with angina pectoris but normal coronary arteriograms.
Circulation 1981;63:817-825
46. Steenbergen C, Deleeuw G, Williamson JR: Analysis of
control of glycolysis in ischemic hearts having heterogeneous
zones of anoxia. J Mol Cell Cardiol 1978;10:617-639
47. Eng C, Cho S, Factor SM, Sonnenblick EH, Kirk ES: Myocardial micronecrosis produced by microsphere embolization.
Circ Res 1984;54:74-82
48. Weiss HR, Conway RS: Morphometric study of the total and
perfused arteriolar and capillary network of the rabbit left
ventricle. Cardiovasc Res 1985;19:343-354
49. Chilian WM, Eastham CL, Marcus ML: Microvascular distribution of coronary vascular resistance in beating left ventricle.
Am J Physiol 1986;251(Heart Circ Physiol 20):H779-H788
KEY WORDS * coronary flow * regional coronary reserve
autocorrelation * continuity
.
Profound spatial heterogeneity of coronary reserve. Discordance between patterns of
resting and maximal myocardial blood flow.
R E Austin, Jr, G S Aldea, D L Coggins, A E Flynn and J I Hoffman
Downloaded from http://circres.ahajournals.org/ by guest on June 14, 2017
Circ Res. 1990;67:319-331
doi: 10.1161/01.RES.67.2.319
Circulation Research is published by the American Heart Association, 7272 Greenville Avenue, Dallas, TX 75231
Copyright © 1990 American Heart Association, Inc. All rights reserved.
Print ISSN: 0009-7330. Online ISSN: 1524-4571
The online version of this article, along with updated information and services, is located on the
World Wide Web at:
http://circres.ahajournals.org/content/67/2/319
Permissions: Requests for permissions to reproduce figures, tables, or portions of articles originally published
in Circulation Research can be obtained via RightsLink, a service of the Copyright Clearance Center, not the
Editorial Office. Once the online version of the published article for which permission is being requested is
located, click Request Permissions in the middle column of the Web page under Services. Further information
about this process is available in the Permissions and Rights Question and Answer document.
Reprints: Information about reprints can be found online at:
http://www.lww.com/reprints
Subscriptions: Information about subscribing to Circulation Research is online at:
http://circres.ahajournals.org//subscriptions/