* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Corresponding angles and corresponding sides are congruent in
Dessin d'enfant wikipedia , lookup
Penrose tiling wikipedia , lookup
Multilateration wikipedia , lookup
Technical drawing wikipedia , lookup
Apollonian network wikipedia , lookup
Rational trigonometry wikipedia , lookup
Euler angles wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Trigonometric functions wikipedia , lookup
History of trigonometry wikipedia , lookup
Pythagorean theorem wikipedia , lookup
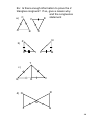
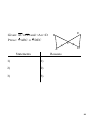
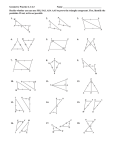
Unit 4: Congruence and Triangles (4.2) p.202211 Congruent Triangles:2 triangles that are exactly the same, both equal in length and equal in angle measure Corresponding angles and corresponding sides are congruent in congruent triangles. see example below Ex: Triangle ABC ≅ Triangle DEF E B D A C F 1 Third Angles Theorem: If 2 angles are congruent in one triangle to 2 angles in another triangle, then the third angle in each triangle will also be congruent B D F A C E If <A≅<D and <B≅<E, then <C≅<E 2 Ex: Solve for x and y I ABCDE≅FGHIJ A 111o E 93o B 15 in. 14 in. 105o D 12 in. C (4x + 7) in. (2y7)o J H G F 3 Ex: Solve for x (5x + 8)o 42o (4x 1)o 4 Properties of Congruent Triangles Reflexive Property of Congruent Triangles: a triangle is congruent to itself ABC ≅ ABC A Symmetric Property of Congruent Triangles : DEF ≅ ABC If ABC ≅ DEF, then D Transitive Property of Congruent Triangles : If and , ABC ≅ DEF DEF ≅ JKL then ABC ≅ JKL J B C E F K L 5 X Ex: Given: XY // WZ XY ≅ WZ V is the midpoint of XZ and WY Prove: YVX ≅ WVZ W V Y Z StatementsReasons 1) XY // WZ, XY ≅ WZ 1) _________________ 2) <YXV≅<VZW <XYV≅<ZWV 2) _________________ 3)__________________ 3) Vertical <'s Theorem 4) V is the mdpt XZ & WY 4)__________________ 5)___________________ 5) __________________ 6) YVX ≅ WVZ 6) __________________ 6 HW: p.206207 #1014 #1621 #2328 7 Unit 4: Proving Triangles are Congruent: SSS & SAS(4.3)p.212219 5 Congruence Postulates and Theorems: THE BIG 5 1: Side Side Side Postulate (SSS) 2: Side Angle Side Postulate (SAS) 3: Angle Side Angle Postulate (ASA) 4: Angle Angle Side Postulate (AAS) 5: Hypotenuse Leg Theorem (HL) 8 SideSideSide (SSS) Postulate: SSS: If 3 sides of one triangle are congruent to the 3 corresponding sides of another triangle, then the two triangles are congruent. D B A C F E 9 SideAngleSide (SAS) Postulate: SAS: If 2 sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then two triangles are congruent. B M N A C L 10 Ex: Given AB≅DB and AC≅DC Prove: ABC≅ DBC A Statements C B D Reasons 1) 1) Given 2) 2) 3) 3) 11 Ex: Given: C is the midpoint of AE and BD B Prove: ABC ≅ EDC E C A Statements D Reasons 1) 1) 2) 2) 3) 3) 4) 4) 12 T Given: UV bisects TW at point V TU≅WU Prove: TVU ≅ WVU V U Statements W Reasons 1) 1) Given 2) V is the midpoint of 2) TW 3) 3) Def. of midpoint 4) 4) Given 5) 5) 6) 6) 13 Ex: Is there enough information to prove the 2 triangles congruent? If so, give a reason why. and the congruence statement C a) E F A B D N Z b) X Y M L T c) V R Q R d) N M L Q 14 HW: p.216217 #1123 all 15 Unit 4: Proving Triangles are Congruent: ASA & AAS (4.4) p.220228 ASA: If 2 angles and the included side of one triangle are congruent to 2 angles and the included side of another triangle, then the 2 triangles are congruent. Z A B C X Y 16 AAS: If 2 angles and a nonincluded side of one triangle are congruent to 2 angles and a nonincluded side of another triangle, then the 2 triangles are congruent. A H C B K J 17 HL: If the hypotenuse and a leg of one right triangle are congruent to a hypotenuse and a leg of another right triangle, then the 2 triangles are congruent. B A C I G H 18 Given: <A≅<C and <ADB and <BDC are right angles Prove: ADB ≅ CDB A Statements 1) 2) <ADB≅<BDC B D C Reasons 1) 2) 3) 3) 4) 4) 19 Given: AC≅CD and <A≅<D Prove: ABC ≅ DEC E B C A Statements D Reasons 1) 1) 2) 2) 3) 3) 20 A Given: AZ≅AX <AYX and <AYZ are right angles Prove: AYZ ≅ AYX Z Reasons Statements 1) 1) 2) 2) 3) 3) 4) 4) Y X 21 E Given: BE bisects <AED <A≅<D Prove: ABE ≅ DBE A Statements B D Reasons 1) BE bisects <AED 1) 2) 2) 3) <A≅<D 3) 4) 4) 5) 5) 22 Ex: Is there enough information to prove the triangles are congruent? If so, explain why? D B a) C E A Y b) Z X W O c) M N P L d) T S Q R 23 HW: p.223224 #822 all 24 Review Congruent TrianglesExtra Practice with THE BIG FIVE: SSS, SAS, ASA, AAS, HL Example 1: Are the 2 triangles congruent? If so, why are they congruent and give the congruence statement. B b) A R Z a) C X Y T Q E D 25 Ex 1: continued c) H e) R E N d) X T S F G A O f) M L O C M E Y N 26 Example 1: continued S D g) A h) U C B Q T i) R j) T D G E F U X W V 27 Unit 4: Using Congruent Triangles (4.5) p.229242 TIDBITS OF INFO There is no Angle Side Side when proving congruent triangles Once you use 1 of THE BIG 5, the reason you can use to say all other parts of triangles are congruent is: Corresponding Parts of Congruent Triangles are Congruent (CPCTC): If 2 triangles are congruent, then all corresponding parts (sides and angles) are also congruent. Vertical angles are always congruent E A <ACB ≅ <ECD C D B Reflexive sides are always congruent N LN ≅ LN M P L Parallel Lines only allow you to say 2 angles are congruent A E <A≅<D <E≅<B C B D A B C <ABC≅<E E D 28 B Given: AB≅BC and AD≅AC Prove: <A≅<C A Reasons Statements 1) 1) 2) 2) 3) 3) 4) 4) D C 29 Given: AB//DC and BD//AC Prove: AB≅CD B A Statements 1) 2) <ABC≅______ <ACB≅______ D C Reasons 1) 2) 3) 3) 4) 4) 5) 5) 30 Given: QR//VT , QR≅VT, and <R≅<T Prove: QV≅VX Q R V T X Statements 1) QR//VT Reasons 1) 2) 2) 3) 3) Given 4) 4) 5) 5) 31 Given: <WVY≅<WXZ and WZ≅WY Prove: <Z≅<Y V Z Reasons Statements 1) 1) 2) 2) 3) 3) 4) 4) W X Y 32 HW: p.232234 #818 all 33