Download 5-1 Bisectors of Triangles

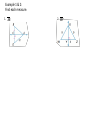
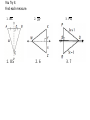
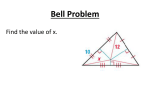
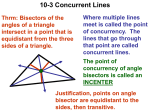
5-1 Bisectors of Triangles
The student will be able to:
1. Identify and use perpendicular bisectors in triangles.
2. Identify and use angle bisectors in triangles.
Perpendicular Bisector Theorem
Segment Bisector:
Perpendicular Bisector:
Perpendicular Bisector Theorem – A point is on the perpendicular
bisector of a segment if and only if it is equidistant from the
endpoints of the segment.
Example 1 & 2:
Find each measure.
1. AB
2. WY
Example 3 & 4:
3. RT
You Try it:
Find each measure.
1. BC
1. 8.5
2. XY
3. PQ
2. 6
3. 7
When three or more lines intersect at a common point, the lines
are called concurrent lines. The point where concurrent lines
intersect is called the point of concurrency.
Circumcenter Theorem – If you draw a perpendicular bisector
from each side of a triangle, the 3 perpendicular bisectors
intersect at a point called circumcenter that is equidistant from
the vertices of the triangle. J is the circumcenter.
The circumcenter will be:
inside
outside
on
Examples 5, 6, & 7:
Example 8:
A stove S, sink K, and refrigerator R are positioned in a kitchen as
shown. Find the location for the center of an island work station so that
it is the same distance from these three points.
You Try It:
Two triangular-shaped gardens are shown below. Determine if a
fountain can be placed at the circumcenter of each garden and still be
inside the garden. Why or Why not?
Angle Bisectors
An Angle Bisector is a special segment, ray, or line that divides an
angle into two congruent angles.
Two properties of angle bisectors are:
1. A point is on the angle bisector of an angle if and only if it is
equidistant from the sides of the angle.
2. The three angle bisectors of a triangle meet at a point,
called the incenter of the triangle, that is equidistant from
the three sides of the triangle. Point K is the incenter of
ΔABC.
You Try It:
If P is the incenter of ΔXYZ, find each measure.
PK =
mÐLZP =