Download Introduction to Monte Carlo Simulation

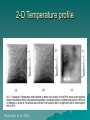
Introduction to Monte
Carlo Simulation
What is a Monte Carlo simulation?
• In a Monte Carlo simulation we attempt to
follow the `time dependence’ of a model
for which change, or growth, does not
proceed in some rigorously predefined
fashion (e.g. according to Newton’s
equations of motion) but rather in a
stochastic manner which depends on a
sequence of random numbers which is
generated during the simulation.
Details of the Method



Random Walk: Markov chain is a sequence of
events with the condition that the probability of
each succeeding event is uninfluenced by prior
events
Choosing from Probability Distribution: Any
random variable has a probability distribution for
its occurrence. We need to choose a random
variable which mimics that probability distribution
Best way to relate random number to a random
variable is to use cumulative probability
distribution and equating it to the random nuber
Random Numbers
 Uniformly
distributed numbers in
[0,1]
 Most useful method for obtaining
random numbers for computer use is
a pseudo random number generator
 How random are these pseudo
random numbers?
Anyone who considers arithmetical
methods of producing random digits is, of
course, in a state of sin.
John von Neumann (1951)
Application to Microscale Heat
Transfer
 Boltzmann
Transport Equation (BTE)
for phonons best describes the heat
flow in solid nonmetallic thin films
 difficult to solve analytically or even
numerically using deterministic
approaches
 alternative is to solve the BTE using
stochastic or Monte Carlo techniques
Boltzmann Transport Equation for Particle Transport
Distribution Function of Particles: f = f(r,p,t)
--probability of particle occupation of momentum p at location r and time t
Equilibrium Distribution:
f0, i.e. Fermi-Dirac for electrons, Bose-Einstein for phonons, Plank for photons, etc.
Non-equilibrium, e.g. in a high electric field or temperature gradient:
f
 f 
 v  r f  F   p f   
t
 t  scat
Relaxation Time Approximation


fo  f
 f 














W
p,
p
f
p

W
p
,
p
f
p

 
 

 
 
   r, p 

t
  scat p  
pp
pp


Relaxation time
f  fo
e
t

t
Monte Carlo Solution Technique
Phonons are drawn from the six individual
stochastic spaces, including three wavevector components and the three position
vector components
 Phonons are then allowed to drift (or
unrestrained motion) and scatter in time,
and their statistics is collected at various
points in time and space, and processed to
extract the necessary information

Initial Conditions
number of phonons per unit volume and
polarization (p) is usually an extremely large
number
 a scaling factor is used to simulate only a
fraction of the phonons
 A series of random numbers properly
distributed to match the equilibrium
distribution are drawn to initialize the
positions, frequencies, polarizations, and
wavevectors of the ensemble of phonons
chosen for the simulation

Initial conditions

Mazumdar and Majumdar developed a
numerical scheme to obtain the number of
phonons within the ith frequency interval
Dw as:
Boundary Conditions
 Isothermal
boundary condition:
Phonons incident on the wall are
removed from the computation
domain and a new phonon is
introduced in the system which
depends on the wall temperature
 Adiabatic boundary condition:
reflects all the phonons that are
incident on the wall
Drift


During the drift phase, phonons move
linearly from one location to another and
their positions are tracked using an explicit
first-order time integration
phonons are tallied within each spatial bin,
and the energy of each spatial bin is
computed and stored
Scattering
Three-Phonon Scattering (Normal and
Umklapp Processes): need to know
scattering time-scales, probability of 3-P
scattering is given by PNU = 1-exp(Dt/tNU)
 A random number is chosen and
compared to the probability, if less then it
is scattered
 If scattered then the new phonon is
generated based on the pseudo
temperature of the cell

Scattering



Scattering by Impurities: Scattering by impurities,
defects and dislocations are treated in the Monte
Carlo scheme in isolation from normal and Umklapp
scattering
The time-scale for scattering due to impurities,i is
given by
where a is a constant of the order of unity, r is the
defect density per unit volume, and s is the
scattering cross-section
Temperature profile for ballistic
transport
2-D Temperature profile
Mazumder et al. 2001
Monte Carlo Simulation of
Silicon Nanowire Thermal
Conductivity
Boundary scattering play an important role in
thermal resistance as the structure size
decreases to nanoscale
Thermal conductivity (W/K.m)

70
115nm
37nm
22nm
60
50
40
30
20
10
0
0
50
100
150
200
250
Temperature (K)
300
350
Heat Generation in Electronic
Nanostructure
Pop E. et al. 2002
Statistical Error
 Monte
Carlo simulation is a
stochastic sampling process, hence
have inherent statistical error
 errors depend primarily on the
number of stochastic samples used
in the simulation and the number of
scattering events that occur
Reference



Mazumder, S. and Majumdar, A., “Monte Carlo study of phonon
transport in solid thin films including dispersion and
polarization,” J. of Heat Transfer, vol. 123, pp. 749-759, 2001
Pop E., Sinha S., Goodson K. E., “Monte Carlo modeling of heat
generation in electronic nanostructures”, 2002 ASME
International Mechanical Engineering Congress and Exposition
Jacoboni, C. and Reggiani., L., “The Monte Carlo method for the
solution of charge transport in semiconductors with applications
to covalent materials,” Reviews of Modern Physics, vol. 55, pp.
645-705, 1983