Download Linear Algebra

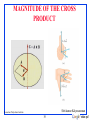
Linear Algebra
A gentle introduction
Linear Algebra has become as basic and as applicable
as calculus, and fortunately it is easier.
--Gilbert Strang, MIT
Shivkumar Kalyanaraman
Rensselaer Polytechnic Institute
1
: “shiv rpi”
What is a Vector ?

Think of a vector as a directed line
segment in N-dimensions! (has “length”
and “direction”)

Basic idea: convert geometry in higher
dimensions into algebra!
 Once you define a “nice” basis along
each dimension: x-, y-, z-axis …
 Vector becomes a N x 1 matrix!
 v = [a b c]T
 Geometry starts to become linear
algebra on vectors like v!
a 
  
v  b 
 c 
y
v
x
Shivkumar Kalyanaraman
Rensselaer Polytechnic Institute
2
: “shiv rpi”
Vector Addition: A+B
vA+B
 w  ( x1 , x 2 )  ( y 1 , y 2 )  ( x1  y 1 , x 2  y 2 )
A
A+B = C
(use the head-to-tail method
to combine vectors)
B
C
B
A
Shivkumar Kalyanaraman
Rensselaer Polytechnic Institute
3
: “shiv rpi”
Scalar Product: av
a v  a ( x1 , x 2 )  ( ax1 , ax 2 )
av
v
Change only the length (“scaling”), but keep direction fixed.
Sneak peek: matrix operation (Av) can change length,
direction and also dimensionality!
Shivkumar Kalyanaraman
Rensselaer Polytechnic Institute
4
: “shiv rpi”
Vectors: Dot Product
d 
A  B  AT B   a b c   e   ad  be  cf
 f 
The magnitude is the dot
product of a vector with itself
A  AT A  aa  bb  cc
2
A  B  A B cos( )
Think of the dot product as
a matrix multiplication
The dot product is also related to the
angle between the two vectors
Shivkumar Kalyanaraman
Rensselaer Polytechnic Institute
5
: “shiv rpi”
Inner (dot) Product: v.w or wTv
v

w
v .w  ( x1 , x 2 ).( y1 , y 2 )  x1 y1  x 2 . y 2
The inner product is a SCALAR!
v .w  ( x1 , x 2 ).( y1 , y 2 )  || v ||  || w || cos 
v .w  0  v  w
If vectors v, w are “columns”, then dot product is wTv
Shivkumar Kalyanaraman
Rensselaer Polytechnic Institute
6
: “shiv rpi”
Projection: Using Inner Products (I)
p = a (aTx)
||a|| = aTa = 1
Shivkumar Kalyanaraman
Rensselaer Polytechnic Institute
7
: “shiv rpi”
Bases & Orthonormal Bases

Basis (or axes): frame of reference
vs
Basis: a space is totally defined by a set of vectors – any point is a linear
combination of the basis
Ortho-Normal: orthogonal + normal
[Sneak peek:
Orthogonal: dot product is zero
Normal: magnitude is one ]
Rensselaer Polytechnic Institute
8
x  1 0 0
y  0 1 0
x y  0
xz  0
z  0 0 1
yz  0
T
T
T
Shivkumar Kalyanaraman
: “shiv rpi”
What is a Matrix?

A matrix is a set of elements, organized into rows and
columns
rows
columns
a b 
c d 


Shivkumar Kalyanaraman
Rensselaer Polytechnic Institute
9
: “shiv rpi”
Basic Matrix Operations

Addition, Subtraction, Multiplication: creating new matrices (or functions)
a b   e
c d    g

 
f  a  e b  f 


h  c  g d  h 
a b   e
c d    g

 
f  a  e b  f 



h  c  g d  h 
a b   e
c d   g


f  ae  bg


h  ce  dg
af  bh
cf  dh 
Just add elements
Just subtract elements
Multiply each row
by each column
Shivkumar Kalyanaraman
Rensselaer Polytechnic Institute
10
: “shiv rpi”
Matrix Times Matrix
L  M N
 l11 l12 l13   m11 m12
l


 21 l22 l23    m21 m22
l31 l32 l33   m31 m32
m13   n11 n12


m23    n21 n22
m33   n31 n32
n13 

n23 
n33 
l1 2  m 1 1 n 1 2  m 1 2 n 2 2  m 1 3 n 3 2
Shivkumar Kalyanaraman
Rensselaer Polytechnic Institute
11
: “shiv rpi”
Multiplication

Is AB = BA? Maybe, but maybe not!
a b   e
c d   g





f  ae  bg ...


h   ...
...
e
g

f  a b  ea  fc ...




h   c d   ...
...
Matrix multiplication AB: apply transformation B first, and
then again transform using A!
Heads up: multiplication is NOT commutative!
Note: If A and B both represent either pure “rotation” or
“scaling” they can be interchanged (i.e. AB = BA)
Shivkumar Kalyanaraman
Rensselaer Polytechnic Institute
12
: “shiv rpi”
Matrix operating on vectors





Matrix is like a function that transforms the vectors on a plane
Matrix operating on a general point => transforms x- and y-components
System of linear equations: matrix is just the bunch of coeffs !
x’ = ax + by
y’ = cx + dy
a b   x   x'

    
c d   y  y'
Shivkumar Kalyanaraman
Rensselaer Polytechnic Institute
13
: “shiv rpi”
Direction Vector Dot Matrix
 ax
a
v  M  v   y
 az

0
bx
by
cx
cy
bz
cz
0
0
d x   vx 
d y  v y 

d z   vz 
  
1  1
vx  vx ax  v y bx  vz cx
v  v xa  v yb  v zc
vy  vx a y  v y by  vz c y
vz  vx az  v y bz  vz cz
Shivkumar Kalyanaraman
Rensselaer Polytechnic Institute
14
: “shiv rpi”
Inverse of a Matrix




Identity matrix:
AI = A
Inverse exists only for square
matrices that are non-singular
 Maps N-d space to another
N-d space bijectively
Some matrices have an
inverse, such that:
AA-1 = I
Inversion is tricky:
(ABC)-1 = C-1B-1A-1
Derived from noncommutativity property
1 0 0


I  0 1 0 
0 0 1
Shivkumar Kalyanaraman
Rensselaer Polytechnic Institute
15
: “shiv rpi”
Determinant of a Matrix


Used for inversion
If det(A) = 0, then A has no inverse
a b 
A

c
d


det( A)  ad  bc
1  d  b
A 
ad  bc  c a 
1
http://www.euclideanspace.com/maths/algebra/matrix/functio
ns/inverse/threeD/index.htm
Shivkumar Kalyanaraman
Rensselaer Polytechnic Institute
16
: “shiv rpi”
Transpose of a Matrix

Written AT (transpose of A)
a b 
A

c
d




a c 
A 

b
d


T
Keep the diagonal but reflect all other elements about the diagonal
aij = aji where i is the row and j the column
in this example, elements c and b were exchanged
For orthonormal matrices A-1 = AT
Shivkumar Kalyanaraman
Rensselaer Polytechnic Institute
17
: “shiv rpi”
Vectors: Cross Product

The cross product of vectors A and B is a vector C which is
perpendicular to A and B

The magnitude of C is proportional to the sin of the angle
between A and B

The direction of C follows the right hand rule if we are
working in a right-handed coordinate system
A  B  A B sin(  )
A×B
B
A
Shivkumar Kalyanaraman
Rensselaer Polytechnic Institute
18
: “shiv rpi”
MAGNITUDE OF THE CROSS
PRODUCT
Shivkumar Kalyanaraman
Rensselaer Polytechnic Institute
19
: “shiv rpi”
DIRECTION OF THE CROSS
PRODUCT

The right hand rule determines the direction of the
cross product
Shivkumar Kalyanaraman
Rensselaer Polytechnic Institute
20
: “shiv rpi”
For more details


Prof. Gilbert Strang’s course videos:
http://ocw.mit.edu/OcwWeb/Mathematics/18-06Spring2005/VideoLectures/index.htm

Esp. the lectures on eigenvalues/eigenvectors, singular value
decomposition & applications of both. (second half of course)

Online Linear Algebra Tutorials:
http://tutorial.math.lamar.edu/AllBrowsers/2318/2318.asp

Shivkumar Kalyanaraman
Rensselaer Polytechnic Institute
21
: “shiv rpi”