Lecture 8. Quaternions
... pq = (p0 + p1 i + p2 j + p3 k )(q0 + q1 i + q2 j + q3 k ) = (p0 q0 − p1 q1 − p2 q2 − p3 q3 ) + . . . i + . . . j + . . . k pq = (p0 + p)(q0 + q) = (p0 q0 + p0 q + q0 p + pq) The last product includes many different kinds of product: product of two reals, scalar product of vectors. But what is pq? Cr ...
... pq = (p0 + p1 i + p2 j + p3 k )(q0 + q1 i + q2 j + q3 k ) = (p0 q0 − p1 q1 − p2 q2 − p3 q3 ) + . . . i + . . . j + . . . k pq = (p0 + p)(q0 + q) = (p0 q0 + p0 q + q0 p + pq) The last product includes many different kinds of product: product of two reals, scalar product of vectors. But what is pq? Cr ...
Linear Algebra - UC Davis Mathematics
... 1. uncover aspects of functions that don’t change with the choice (Ch 12) 2. make calculations maximally easy (Ch 13 and Ch 17) 3. approximate functions of several variables (Ch 17). Unfortunately, because the subject (at least for those learning it) requires seemingly arcane and tedious computation ...
... 1. uncover aspects of functions that don’t change with the choice (Ch 12) 2. make calculations maximally easy (Ch 13 and Ch 17) 3. approximate functions of several variables (Ch 17). Unfortunately, because the subject (at least for those learning it) requires seemingly arcane and tedious computation ...
Linear Algebra - Cornell Computer Science
... Here are my online notes for my Linear Algebra course that I teach here at Lamar University. Despite the fact that these are my “class notes” they should be accessible to anyone wanting to learn Linear Algebra or needing a refresher. These notes do assume that the reader has a good working knowledge ...
... Here are my online notes for my Linear Algebra course that I teach here at Lamar University. Despite the fact that these are my “class notes” they should be accessible to anyone wanting to learn Linear Algebra or needing a refresher. These notes do assume that the reader has a good working knowledge ...
Linear Algebra in Twenty Five Lectures
... like Jill, how much does Andrew like Andrew, etcetera). We could arrange these in a square array ...
... like Jill, how much does Andrew like Andrew, etcetera). We could arrange these in a square array ...
... rarely defined carefully, and the definition usually has to do with transformation properties, making it difficult to get a feel for what these objects are. Furthermore, physics texts at the beginning graduate level usually only deal with tensors in their component form, so students wonder what the ...
Vector Spaces
... x2 axis; cf. Figure 2.5. Every vector, which we picture as an arrow emanating from the origin, is uniquely determined once we know where its tip is located. This means that every vector can be uniquely associated with an ordered pair of numbers. In other words, two vectors are equal if and only if t ...
... x2 axis; cf. Figure 2.5. Every vector, which we picture as an arrow emanating from the origin, is uniquely determined once we know where its tip is located. This means that every vector can be uniquely associated with an ordered pair of numbers. In other words, two vectors are equal if and only if t ...
Math 304 Answers to Selected Problems 1 Section 5.5
... (b) Solve the least squares problem Ax = b for each of the following choices of b. (i) b = (4, 0, 0, 0)T (ii) b = (1, 2, 3, 4)T (iii) b = (1, 1, 2, 2)T Answer: (a) Let a1 and a2 denote the first and second column vectors of A, respectively. To show that the column vectors of A form an orthonormal s ...
... (b) Solve the least squares problem Ax = b for each of the following choices of b. (i) b = (4, 0, 0, 0)T (ii) b = (1, 2, 3, 4)T (iii) b = (1, 1, 2, 2)T Answer: (a) Let a1 and a2 denote the first and second column vectors of A, respectively. To show that the column vectors of A form an orthonormal s ...
Cross product
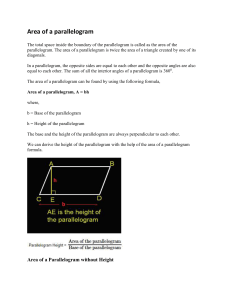
In mathematics and vector calculus, the cross product or vector product (occasionally directed area product to emphasize the geometric significance) is a binary operation on two vectors in three-dimensional space (R3) and is denoted by the symbol ×. The cross product a × b of two linearly independent vectors a and b is a vector that is perpendicular to both and therefore normal to the plane containing them. It has many applications in mathematics, physics, engineering, and computer programming. It should not be confused with dot product (projection product).If two vectors have the same direction (or have the exact opposite direction from one another, i.e. are not linearly independent) or if either one has zero length, then their cross product is zero. More generally, the magnitude of the product equals the area of a parallelogram with the vectors for sides; in particular, the magnitude of the product of two perpendicular vectors is the product of their lengths. The cross product is anticommutative (i.e. a × b = −b × a) and is distributive over addition (i.e. a × (b + c) = a × b + a × c). The space R3 together with the cross product is an algebra over the real numbers, which is neither commutative nor associative, but is a Lie algebra with the cross product being the Lie bracket.Like the dot product, it depends on the metric of Euclidean space, but unlike the dot product, it also depends on a choice of orientation or ""handedness"". The product can be generalized in various ways; it can be made independent of orientation by changing the result to pseudovector, or in arbitrary dimensions the exterior product of vectors can be used with a bivector or two-form result. Also, using the orientation and metric structure just as for the traditional 3-dimensional cross product, one can in n dimensions take the product of n − 1 vectors to produce a vector perpendicular to all of them. But if the product is limited to non-trivial binary products with vector results, it exists only in three and seven dimensions. If one adds the further requirement that the product be uniquely defined, then only the 3-dimensional cross product qualifies. (See § Generalizations, below, for other dimensions.)























