Download Term Structure of Interest rate

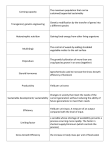
Term Structure of Interest rate
- GROUP 1, TEAM 5
YUDHAJEET BANERJEE – 206
VINAY CHOKHRA – 209
AMIT MEHTA – 220
SRIKANTH REDDY – 225
NIKHIL SHETTY – 234
AMAR BHARTIA – 255
MAHESH KANKANI – 256
Agenda
 Definition of Yield and Yield Curve
 Types & Shifts in Yield Curve
 Theories of Term Structure
 Models for Term Structure of Interest rates
 Investor Behavior
 Interest Rate Risks
 Yield Curve Strategies
Definition of Yield
 A bond’s yield is a measure of its potential return given certain
assumptions about how the future will unfold.
 Interest rates are pure prices of time, and are the discounting factors
used in the valuation equation for bonds.
 We generally associate yield to maturity as our standard meaning for
yield, but there are other forms of yield:



Current Yield
Yield to call
Yield to worst
Definition of Yield Curve
 In finance, the yield curve is the relation between the interest
rate (or cost of borrowing) and the time to maturity of the debt
for a given borrower in a given currency
 A key function of the yield curve is to serve as a benchmark for
pricing bonds and to determine yields in all other sectors of the
debt market ( corporates, agencies, mortgages, bank loans, etc.).
Example of Yield Curve
Source - FIMMDA
Types of Yield Curve

Normal or Upward Sloping Yield Curve

Reflects the higher inflation-risk premium

Reflects investor's expectations for the
economy to grow

Deflation makes Future cash flows more
valuable

Inverted or Downward Sloping Yield Curve
 Long run interest rates are below short term
interest rates.

Reflects investor's expectations for the
economy to slow or decline.
Types of Yield Curve (cont.…)

Flat Yield Curve

Short term interest rates are equal to long term
interest rates.

Small or negligible difference between short and
long term interest rates occurs later in the
economic cycle when interest rates increase due to
higher inflation expectations and tighter monetary
policy.
 Humped Yield Curve

Market expects that interest rates will
first rise (fall) during a period and fall
(rise) during another.
Terms associated with Yield Curves
Parallel
shift
• Interest rates change by the same amount for bonds of all
terms, this is called a parallel shift in the yield curve since
the shape of the yield curve stays the same, although
interest rates are higher or lower across the curve.
Twist
• A change in the shape of the yield curve is called a twist
and means that interest rates for bonds of some terms
change differently than bond of other terms.
Steep
• The difference between long and short term interest rates
is large, the yield curve is said to be steep
Shift in Yield Curve

If the interest rates of all

If the short term interest

If the medium term
maturities are changed by
rates are increased by
interest rates are
identical amounts then
much larger amounts
increased by much larger
there will be a parallel
than the longer term
amounts than the longer
shift in the yield curve.
interest rates, the yield
term interest rates, the
curve becomes less steep
yield curve becomes more
and its slope decreases
hump shaped
Theories of Term Structure
 Expectations Theory (Pure Expectations Theory)

Explains the yield curve as a function of a series of expected forward rates

Implies that the expected average annual return on a long term bond is the geometric mean
of the expected short term rates

Bonds are priced so that the implied forward rates are equal to the expected spot rates

If short term rate are expected to rise in the future, interest rate yields on longer maturities
will be higher than the those of the shorter maturities – upward sloping yield curve
 Liquidity Preference Theory

Places more weight on the effects of the risk
preferences of market participants

Theory asserts that risk aversion will cause forward
rates to be systemically greater than expected spot
rates

Longer-term interest rates not only reflect
investors’ future assumptions for the interest rates,
but also includes a premium for holding these
longer-term bonds
Theories of Term Structure (cont.…)


Market Segmentation Theory (Segmented Markets
Theory)

Based on the idea that investors and borrowers have
preferences for different maturity stages

The demand and supply of bonds of particular maturity
are little affected by the bonds of neighboring
maturities’ prices

E.g.. Institutional investors may have preference for
maturity ranges that closely match their liabilities etc.
Preferred Habitat Theory

Similar to market segmentation theory

Investors have preference for particular maturity but can be induced to move from their preferred
maturity ranges when yields are sufficiently higher in other (non-preferred) maturity ranges

They will move only if they are compensated for the additional risk
Economic v/s Statistical Models
 Economic models are designed to match correlations between interest rates
and other economic aggregate variables


Pro: Economic (structural) models use all the latest information available to predict interest
rate movements
Con: They require a lot of data, the equation can be quite complex, and over longer time
periods are very inaccurate
 Statistical models are designed to match the dynamics of interest rates and the
yield curve using past behavior.


Pro: Statistical Models require very little data and are generally easy to calculate
Con: Statistical models rely entirely on the past. They don’t incorporate new information
Term Structure of Interest Rates: Development of
Mathematical Models
CIR Model
Hull White
Model
• Established in
1977
• Established in
1985
• Established in
1990
• Established in
1992
• One factor
Short Rate
model
• Extension of
the Vasicek
Model
• Impacted by
the current
volatilities of
all spot interest
rates and all
forward
interest rates
• Very general
interest rate
framework
Vasicek Model
Heath, Jarrow,
Morton Model
• Automatically
calibrated to
the initial yield
curve
Vasicek Model
dit     it dt  dz
Controls Persistence
Controls Mean
Controls Variance
(Randomness Factor)
 Indicates the long term mean level of interest rates

Indicates the speed of reversion". It characterizes the velocity at which
such trajectories will regroup around

Advantage: Vasicek's model was the first one to capture mean reversion
Disadvantage: It is theoretically possible for the interest rate to become negative
Using the Vasicek Model



Choose parameter values
Choose a starting value
Generate a set of random numbers with mean 0 and variance 1



Parameter Values:
Kappa= 0.2
Sigma= 2
t=0
t=1
t=2
t=3
t=4
i
6%
6.8%
6.84%
4.202%
5.5616%
.2(6-i)
0
-.16
-.168
.3596
dz
.4
.2
-1.1
.5
di
.8
.04
-2.368
1.3596
-.9
Cox–Ingersoll–Ross model (CIR) Model
The CIR framework allows for volatility that depends on the current level of the interest
rate (higher volatilities are associated with higher rates)
The standard deviation factor avoids the possibility of negative interest rates
When the rate is at a low level (close to zero), the standard deviation also becomes close
to zero, which dampens the effect of the random shock on the rate. Consequently, when
the rate gets close to zero, its evolution becomes dominated by the drift factor, which
pushes the rate upwards (towards equilibrium).
Factors for changes in Interest Rates
 Inflation
 Changes in the supply and demand of credit
 Reserve Bank of India policy
 Fiscal policy
 Fluctuations in Exchange rates
 Economic conditions
 Market psychology
Behavior to changes in Interest rates
Investor
•Long term investors tend to hold
till maturity as the prices of
existing bonds fall
•Short term investors may reduce
the average maturity of holdings
by swaps to shorter maturity
bonds
•Short term investors may sell the
bonds for capital gains as prices
for existing bonds rise
•Long Term Investors may extend
the maturity of their holdings and
increase the call protection and
decrease reinvestment risk
Interest Rates
Issuer
•Pays a competitive interest rate
to get people to buy new bonds
Increase
•Bond issuers may redeem
existing debt (Callable option)
and issue new bonds at a lower
interest rate
Decrease
Investor Risks
Bond Portfolio Strategy
 Selection of the most appropriate strategy involves picking one
that is consistent with the objectives and policy guidelines of the
client or institution.
 Basic types of strategies:
 Active


Laddered

Barbell

Bullet
Passive

Buy and hold

Indexing
Matched-funding strategies
 Contingent procedures (structured active management)

Bond Portfolio Strategy (cont.…)
 Passive Portfolio Strategies
 Buy and hold
 Maximize the income generating properties of bonds
 The premise of this strategy is that bonds are assumed to be safe
 Investors Hold them to maturity
 Indexing
 Indexing is considered to be quasi-passive by design.
 The main objective of indexing a bond portfolio is to provide a return and risk
Characteristic closely tied to the targeted index
 Matched-funding strategies
 Dedicated portfolio – exact cash match
 Contingent procedures (structured active management)
 Contingent immunization`
Non-parallel shifts - Butterfly
Positive Butterfly
Short
Intermediate
Maturity
Long
Negative Butterfly
Short
Intermediate
Maturity
Long
Butterfly
Yield
Positive
butterfly
Yield Curve
Negative
Butterfly
Term to Maturity
Yield Curve Strategies
Bullet Strategy
Barbell Strategy
Ladder Strategy
Barbell Strategy
 A barbell allows the investor to hedge against both interest rate
and reinvestment risk


If rates go up, the short portion of the barbell can be reinvested at the
higher rate and help offset losses in the longer maturity.
If rates decline, the long maturity gains make up for the lower
interest rate available for reinvestment of the short maturity portion.
 Can be used to create a portfolio with the same duration as a
bullet strategy but with higher convexity.


If interest rates fall, then convexity will augment the rise in the price
of the bond.
If interest rates rise, convexity will dampen the decline in price.
Ladder Strategy
 Environment in which interest rates are rising
 The investor can reinvest the proceeds of the maturing bonds
at the new (higher) interest rate.
 Environment in which interest rates are falling
 The investor will reinvest the proceeds at a lower rate, but only
for 10% of the portfolio.
 The longer maturity bonds would rise in value.
 Advantages
 Since it continues to roll over into cash it provides flexibility
 Reduces Investment income fluctuations
 Requires little investment expertise
 Not locked onto a single bond
References
 Frank J. Fabozzi, Ed., The Handbook of Fixed-Income Securities,
6th Edition (New York, NY: McGraw Hill, 2000)
 Annette Thau, The Bond Book, 2nd Edition (New York, NY:
McGraw Hill, 2001)
 Ali Irturk, Term Structure of Interest Rates, Spring 2006
 www.fimmda.org
 www.nseindia.com
 www.rbi.gov.in
Thank You!