Download 8-1 Geometric Mean

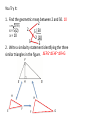
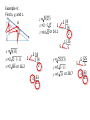
8-1 Geometric Mean
The student will be able to:
1. Find the geometric mean between two numbers.
2. Solve problems involving relationships between parts of a
right triangle and the altitude to its hypotenuse.
Geometric Mean
The geometric mean of two positive numbers a and b is the
positive square root of their product (x).
x = ab
The geometric mean is created
when a proportion is set up, crossmultiplied and solved for x.
The geometric mean of a = 9 and b = 4 is
found by:
2 |4
x = ab
2
x = 9(4)
2
x = 3·2
3 |9
3
x=6
3
x(x) = a(b)
x2 = ab
x = ab
Example 1:
Find the geometric mean between 5 and 45.
x = 5(45)
x = 5(3)
x = 15
5
3
5
5 |45
3 |9
3
Geometric Means in Right Triangles
In a right triangle, an altitude drawn from the vertex of the right
angle to the hypotenuse forms two additional right triangles.
These three right triangles are all similar.
1st – Draw the two smaller triangles
to look like the original. (Hint:
match the right angles then match
the shorter side)
2nd – Write similarity statements
for the three triangles.
ΔACB~ ΔADC~ΔCDB
D
D
A
C
C
B
Example 2:
Write a similarity statement identifying the three similar right
triangles in the figure.
1st – Draw the two smaller triangles
to look like the original. (Hint:
match the right angles then match
the shorter side)
M
K
2nd – Write similarity statements
for the three triangles.
ΔKML~ΔKPM~ΔMPL
P
L
M
P
Example 3:
Write a similarity statement identifying the three similar right
triangles in the figure.
1st – Draw the two smaller triangles
to look like the original. (Hint:
match the right angles then match
the shorter side)
Q
2nd – Write similarity statements
for the three triangles.
ΔQSR~ ΔQTS~ ΔSTR
T
S
S
T
R
You Try It:
1. Find the geometric mean between 2 and 50. 10
2
x = 2(50)
2
x = 5(2)
5 |50
x = 10
2 |10
5
5
2. Write a similarity statement identifying the three
similar triangles in the figure. ΔEFG~ΔEHF~ΔFHG
H
E
H
F
F
G
Since we know that an altitude drawn to the hypotenuse of a right
triangle forms 3 similar triangles, you can write proportions
comparing the side lengths of these triangles.
The Geometric Mean (Altitude) Theorem:
The length of the altitude is the geometric
mean between the two lengths of the
hypotenuse or h = xy
The Geometric Mean (leg) Theorem:
The length of the leg is the geometric mean
between the hypotenuse and the segment
adjacent to that leg or b = xc or a = yc
Example 4:
Find x, y, and z.
z = 8(25)
z = 2·5 2
2
z =10 2 or 14.1
33
x = 8(33)
2
x = 2 2·3·11
x = 2 66 or 16.2
2 |8
2 |4
2
5 |25
5
5
2 |8
2 |4
2
3 |33
11
y = 25(33)
y = 5 3·11
y = 5 33 or 28.7
5 |25
5
5
3 |33
11
Example 5:
Find x, y, and z.
12 = 9x
12 = 3 x
x+9
3
12
= x
3
42 = x
3 |9
3
x
16 = x
y = 16(16 + 9)
2 |16
y = 16(25) 2
2 |8
y = 2·2·5
2 |4
2
y = 20
2
5 |25
5
5
z = 9(16 + 9)
z = 9(25)
3
z = 3·5
z = 15
5 |25
5
5
3 |9
3
You Try It:
1. Find c, d, and e.
c =12 5, d = 6 5, e =12
3 |24
e = 6(24)
2 |8
e = 2·2·3
2 |4
2
e =12
3
2
3 |6
2
2
|24
3
24(30)
c=
2 |8
c = 2·2·3 5
2 |4
2
c =12 5
2
2
5 |30
3
3 |6
2
30
d = 6(30)
d = 3·2 5
d=6 5
3
2
3 |6
2
5 |30
3 |6
2