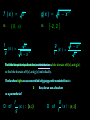Download 1.8 - Villa Walsh Academy

SFM Productions Presents:
Another exciting episode in your continuing Pre-Calculus
experience!
1.8
Combinations of Functions:
Composite Functions
Homework for section 1.8
P88
13-27, 37-59, 73
Two functions may behave exactly like two numbers
in that they may be added, subtracted, multiplied,
and divided.
(f
 g)( x )  f ( x )  g( x )
(f
 g)( x )  f ( x )  g( x )
(f g)( x )  f ( x )
f

g


f (x )
 (x ) 

g( x )


g( x )
Lets say the we have the following functions:
f(x) = x+5 g(x) = 3x
f(x) + g(x) = ?
(f+g)(x) = 4x+5
f(x)  g(x) = ?
(f  g)(x) = 3x2+15x
(f  g)(-5) = ?
f ( 5 )  ( 5 )  5
and g( 5 )  3 ( 5 )
f ( 5 )  0 and g( 5 )  15
 (f
 g)( 5 )  0
f (x ) 
[ 0 , )
D:
f
g
g( x ) 
x
x  
D:
4  x2
2 , 2 
x
4  x
g
2
f
x  
4  x2
x
Find
thethe
domain
each
of these
combinations…
To find
quotients’
domains,
we
first have of the domain of f(x) and g(x).
The
domain
of theofquotient
is the
intersection
to find the domain of f(x) and g(x) individually.
rightwewecan
caneven
eventhink
thinkofofgoing
goingononthe
thenumber
numberline
lineis:is:
The farthest left
20
But, do we use a bracket
or a parenthesis?
D of
f
g
x  :
[0, 2)
D of
g
f
 x  : (0 , 2]
It’s important to remember:
ANY restriction on functions f and g
MUST be considered when forming the:
Sum, Difference, Product, or Quotient of f and g.
Composition of Functions : just another way to combine functions…
If f(x) = x2 and g(x) = x + 1 , then the
composition of f with g is:
(f o g)(x) - pronounced “the f of the g of x”. (Or as I like to call it: fog x.) 
(f o g)(x) = f(g(x))
= f(x + 1)
Do this by working from the inside out…
* Domain of f o g is all x values in the domain
of g where g(x) is in the domain of f.
what the heck does that mean?????
= (x + 1)2
L et
f
x   x 2  9
and
g( x ) 
9  x2
a) find (f o g)(x)
b) find the domain of (f o g)(x)
 g( x ) 
 f
a)
f
b)
-3  x  3

9  x
or, in int erval not at ion:
2
 

9  x
2

2
9
 x 2
 3 , 3 
Why? The domain of g(x) is [-3,3]. These
are the only values you can even think of trying to fit into the domain of (f o
g)(x).
L et
f
1
x  
x 2
and
g( x ) 
x
a) find (f o g)(x)
b) find the domain of (f o g)(x)
 g( x ) 
f



1
x 2
a)
f
b)
all non-negat ive numbers ex cept f or x  4.
x
g( x ) do main
added t o f it
t he (f
D:
[ 0 , 4) , (4, )
g)( x ) domain
Identifying a composite function: it is used in calculus - need to be able to
determine which two functions make up the composite function.
You must be the function…………
Ex p ress h  x  
1
x
2

2
as a comp osit ion
of t w o ot her f unct io ns.
This means we must find: f(x) and g(x) such that their composition gives us
h(x)…
so that: (f o g)(x) =h(x)
"Find" t he inner f unct ion f irst ( t he g( x ) ), an d t hen t he
out t er ( t he f (x ) ).
h x  
1
x
2

2
L et s let g  x  
L et s let f  x  
Go! Do!