Download 2.07 Reversing Operations

GET READY BEFORE THE BELL RINGS!


Take out homework and a pencil to prepare for
the homework quiz!
Check the file folder for your class to pick up
graded work
Located by the bookshelf, blue crate.
 Look behind the tab for your class period and take
home anything with your name on it.

2.07 REVERSING OPERATIONS
Goals:
• Reverse,
or undo, a series of steps
• Understand the relationships between
opposite operations such as addition
and subtraction or multiplication and
division.
• Use backtracking to solve a problem.
LAUNCH
Turn to page 120 in your
textbook.
Read through the list of
reversible actions and operations.
Last week we investigated the
examples given here for
operations that cannot be
reversed. Read about proving by
counterexample.
MINDS IN ACTION
Pair up with another student and
read Tom and Takashi’s
conversation on page 121.
FOR DISCUSSION 1
What did Takashi do wrong?
What number do you think Tom
chose?
Takashi didn’t realize that 169 is
the square of two numbers; –13
THINKING FURTHER
In general, the operation of
“unsquaring,” or taking the square
root of, an unknown number is not
reversible since there are two
numbers with the same output.
Specifically, the second number is
the opposite of the first.
For example, find the two numbers
with a square of 121.
11 and –11
EXAMPLE
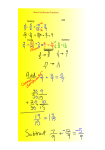
Problem: Find the value of x that
solves the equation 3x – 14 = 37.
Solution: Use backtracking to solve the
equation. We read this equation as, “Three
times some starting number, minus 14, is
equal to 37.” The equation is like one of
Spiro’s number tricks.
Step 1: write the steps, in order, that show
how to get from the input variable x to the
output value 37.
EXAMPLE
Step 2: make a list that reverses the order
of the 1st list and shows how to undo each
operation (reverse the machine).
37
Step 3: start with the output and go
through the list of reverse steps to find the
value of the input variable x.
37 + 14 = 51
51 ÷ 3 = 17
x = 17
DEVELOPING HABITS OF MIND
SUMMARY: ESTABLISH A PROCESS
Step 1: make a list of steps, in order, that
show how to get from the input variable to
the output. Alternatively, you can build a
machine diagram or a flowchart to show
your steps.
Step 2: make a list that reverses the order
of the 1st list and shows how to undo each
operation (reverse the machine or flow
chart).
Step 3: start with the output. Perform each
step on the list of reverse steps (or go
through the reverse machine) to find the
value of the input variable.
FOR DISCUSSION 2
Derman solves an equation such as 3x – 14 = 37
by making a guess, checking it, and then making
a better guess until he finds the solution.
Compare Derman’s method with the backtracking
method. What advantages does backtracking
have? Are there any disadvantages to
backtracking?
Sample answer: backtracking has the advantage
of always leading to the correct solution for
certain types of equations. sometimes,
backtracking can involve an unnecessarily long
series of steps. For example, 2  (10 – x) = 0 has
an obvious solution—what is it?
x = 10
CHECK YOUR UNDERSTANDING 1

Find a partner. Each person thinks of a number.
Take your number and follow these steps (don’t
show your partner!):






Add 6
Divide by 4
Multiply by 8
Add 7
Multiply by 10
Exchange only your ending number with your
partner, and find his/her starting number.
CHECK YOUR UNDERSTANDING 2
Write each algebraic expression as a statement of
one or more operations. For each operation that is
reversible, describe the reverse operation.
Check answers:
n + 13
b) b/–2
c) 3(5m – 12)
d) 15m – 36
a)
“Add 13 ”; subtract 13.
b) “Divide by –2 ”; multiply by –2
c) “Multiply by 5, subtract 12, and
then multiply by 3” ; divide by 3,
add 12, and then divide by 5.
d) “Multiply by 15 and then subtract
36” ; add 36 and then divide by 15.
a)
CHECK YOUR UNDERSTANDING 3
2
Here is a table for the input and output of y  x ,
where x has integer values from –4 to 4. Some
values are missing from the table.
Copy and complete the table.
CHECK YOUR UNDERSTANDING 3
Your table should look like this:
ANSWER THESE QUESTIONS
1.
From your table, how do you know that squaring is
not a reversible operation?
All the outputs except zero have more than one input.
2.
Now add another column to your table for cubing
the input, label the column “ Output, x 3 ”. Is this
operation reversible?
Yes, because each output came from only one input.
3.
Make tables for the outputs of x4 , x5 , x6 , and x7 . Which
powers produce reversible operations?
All the odd powers are reversible.
4.
Why is the result  3 positive? What powers of –3
produce negative numbers?
4
Because when we multiply a negative number an even amount of
times, the product is positive. All odd powers of –3 are negative.
CHECK YOUR TABLES
2.08 SOLVING EQUATIONS BY
BACKTRACKING
Goals:
• Understand
the relationships between
an equation and its solutions.
• Use backtracking to solve a problem.
• Understand basics of equations,
including when equations are always
true and when they are always false.
LAUNCH
Consider the following equations.
x + 4 = 7, 2x + 2 = 2(x + 1), x = x + 1
• Is
x = 3 a solution of any of the
equations?
Yes; the first two equations.
• Is x = 10 a solution?
Yes; the second equation.
• How
many solutions does each
equation have?
The first equation has only one solution, the second
equation is true for all values of x, and the third is never
true.
DEFINITIONS
Equation
An equation is a mathematical
sentence stating that two quantities
are equal.
This definition doesn’t state that an
equation must be true; it only states that it
is a complete thought about numbers. For
example, the equation 3 + 4 = 7 is true, but
2 + 1 = 9 is an equation that’s false.
Solutions
The values of the variables that make
an equation true are solutions of the
equation.
FOR DISCUSSION
1.
How do you know that x + y = y + x is
always true? Commutative Property of
Addition.
2.
How do you know that 𝑥 2 = 𝑥 ∙ 𝑥 is
always true? By definition of squaring a number.
3.
How do you know that x = x + 1 is
always false? No number can equal more than itself.
EXAMPLE 1
Why is the value 3 a solution to the equation x + 4 = 7?
The value 3 is a solution to the equation because it
makes the equation true. Any other value makes the
equation false, so 3 is the only solution.
You can use the term solution set for the collection
of all solutions of an equation. The equation 𝑥 2 = 9
has the solution set {-3, 3}.
When an equation is always false, it has no solutions.
We can say the solution set is the empty set, or null
set.
To find out if a number is a solution to an equation,
just test it out. A variable such as x represents a
number, so every time you see an x in an equation,
replace it with the same number. If you get a true
statement, that number is a solution.
EXAMPLE 2
Is the number 7 a solution to the equation 3x – 28 =
46?
Replace x with 7 to determine if the result is true.
3 ∙ 7 − 28 ≟ 46
21 – 28 ≟ 46
−7 ≠ 46
7 is not a solution to the equation above.
FOR DISCUSSION
4.
Suppose you want to find the solution to 3x – 28 =
46 by guessing. How can you do it?
5.
Can you solve this equation by backtracking?
6.
Suppose you want to find both solutions to
𝑥 2 − 𝑥 − 2 = 0. How can you do this?
EXAMPLE 3
𝑞
3
Solve the equation to find the value of q. 81 = + 76
Suppose you divide the starting number q by 3 and
then add 76. Backtrack by reversing each step in the
opposite order. To find q, start with the ending
number, 81, and follow these steps:
 Subtract 76
81 − 76 = 5
 Multiply by 3
5 ∙ 3 = 15
The starting value of q is 15. After the 1st backtracking step,
𝑞
the remaining equation is 5 = . You find the value of q by
3
multiplying.
Verify the solution in the original equation.
FOR DISCUSSION
7.
8.
Solve the equation 3(a – 1) – 5 = 34.
a = 14
Explain why backtracking helps you solve the
equation above. Use the phrase “reversible
operations.”
You can use backtracking because all the steps involved
in undoing the equation to get from a to 34 were
reversible operations. All the steps we took above in
solving the equation were reversible operations.
CHECK YOUR UNDERSTANDING
Turn to pages 128-129 in your book and work to
complete the following problems:
# 3, 5, 6, and 7