* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lect08
History of electrochemistry wikipedia , lookup
Magnetic monopole wikipedia , lookup
Lorentz force wikipedia , lookup
Electrostatic generator wikipedia , lookup
Maxwell's equations wikipedia , lookup
Faraday paradox wikipedia , lookup
Electric current wikipedia , lookup
Electromotive force wikipedia , lookup
Nanofluidic circuitry wikipedia , lookup
Electricity wikipedia , lookup
Static electricity wikipedia , lookup
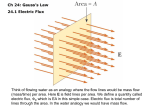
c a b Gauss’ Law •Choose either E dS E dS EdS or E dS E dS 0 •And E constant over surface • is just the area of the Gaussian surface over which we are integrating. •Gauss’ Law •This equation can now be solved for E (at the surface) if we know qenclosed (or for qenclosed if we know E). Gaussian Surfaces Given an infinite sheet of charge as shown in the figure. You need to use Gauss' Law to calculate the electric field near the sheet of charge. Which of the Gaussian surfaces are best suited for this purpose? • a cylinder with its axis along the plane? – • No, E not parallel or perpendicular to the cylinder a cylinder with its axis perpendicular to the plane? – Yes • a cube? – • Yes a sphere? – No Infinite sheet of charge • Symmetry: +s direction of E = x-axis • Therefore, CHOOSE Gaussian surface to be a cylinder whose axis is aligned with the x-axis. • Apply Gauss' Law: • On the barrel, • On the ends, • A x E E The charge enclosed = s A Therefore, Gauss’ Law Conclusion: An infinite plane sheet of charge creates a CONSTANT electric field . Two Infinite Sheets (into the screen) • Field outside must be zero. Two ways to see: – Superposition – Gaussian surface encloses zero charge • Field inside is NOT zero: – Superposition – Gaussian surface encloses non-zero charge 0 - + E=0 s E=0 s - + + + + A + + + + + A + + E Question 1 The figure shows a Gaussian surface enclosing charges 2q and –q. The net flux through the surface is: a) q/0 b) 2q/0 -q 2q c)-q/0 d)zero Question 1 1. 2. 3. 4. a b c d Question 1 The figure shows a Gaussian surface enclosing charges 2q and –q. The net flux through the surface is: a) q/0 b) 2q/0 -q 2q c)-q/0 d)zero •The net charge enclosed is +q. Gauss’ Law says the flux through the surface is q/0 •q of the lines from the positive charge go to the negative charge •q go to infinity and thus pass through the surface Gauss’ Law: Help for the Problems • How to do practically all of the homework problems • • Gauss’ Law is ALWAYS VALID! What Can You Do With This? If you have symmetry (a) spherical, (b) cylindrical, or (c) planar AND: • If you know the charge (RHS), you can calculate the electric field (LHS) • If you know the field (LHS, usually because E=0 inside conductor), you can calculate the charge (RHS). Gauss’ Law: Help for the Problems Spherical Symmetry: Gaussian surface = Sphere of radius r • q = ALL charge inside radius r Cylindrical symmetry: Gaussian surface = cylinder of radius r • q = ALL charge inside radius r, length L • Planar Symmetry: Gaussian surface = Cylinder of area A q = ALL charge inside cylinder =s A Example 1: spheres • A solid conducting sphere is concentric with a thin conducting shell, as shown • The inner sphere carries a charge Q1, and the spherical shell carries a charge Q2, such that Q2 = -3Q1. Q2=-3Q1 Q1 R1 A • How is the charge distributed on the sphere? B • How is the charge distributed on the spherical shell? C • What is the electric field at r < R1? Between R1 and R2? At r > R2? D • What happens when you connect the two spheres with a wire? (What are the charges?) R2 • How is the charge distributed on the sphere? A Q2=-3Q1 * The electric field inside a conductor is zero. (A) By Gauss’s Law, there can be no net charge inside the conductor, and the charge must reside on the outside surface of the sphere + + + + R1 R2 + + + Q1 + B • How is the charge distributed on the spherical shell? Q2=-3Q1 * The electric field inside the conducting shell is zero. (B) There can be no net charge inside the conductor, therefore the inner surface of the shell must carry a net charge of -Q1, to cancel the inner conductor charge. The outer surface must carry the charge +Q1 + Q2, so that the net charge on the shell equals Q2. Q1 The charges are distributed uniformly over the inner and outer surfaces of the shell, hence s inner Q1 2 4R2 and s outer Q2 + Q1 2Q1 2 2 4R2 4R2 R1 R2 C • What is the Electric Field at r < R1? Between R1 and R2? At r > R2? * The electric field inside a conductor is zero. (C) r < R1: Inside the conducting sphere (C) Between R1 and R2 : R1 < r < R2 Charge enclosed = Q1 (C) r > R2 Charge enclosed = Q1 + Q2 Q2=-3Q1 Q1 R1 E 0. R2 1 Q1 E rˆ 2 4 0 r 1 Q1 + Q 2 1 2Q1 E rˆ rˆ 2 2 4 0 r 4 0 r • What happens when you connect the two spheres with a wire? (What are the charges?) D Q2=-3Q1 Q1 R1 After electrostatic equilibrium is reached, there is no charge on the inner sphere, and none on the inner surface of the shell. The charge Q1 + Q2 on the outer surface remains. - - - - - - - - R2 - - - - Also, for r < R2 and for r > R2 E 0. 2Q1 E rˆ 2 4 0 r 1 Are Gauss’ and Coulomb’s Laws Correct? The table shows the results of such experiments looking for a deviation from an inverse-square law: Are Gauss’ and Coulomb’s Laws Correct? •One problem with the above experiments is that they have all been done at short range, 1 meter or so. •Other experiments, more sensitive to cosmic-scale distances, have been done, testing whether Coulomb’s law has the form: •No evidence for a nonzero μ has been found. Example 2: Cylinders An infinite line of charge passes directly through the middle of a hollow, charged, CONDUCTING infinite cylindrical shell of radius R. We will focus on a segment of the cylindrical shell of length h. The line charge has a linear charge density l, and the cylindrical shell has a net surface charge density of stotal. stotal l R sinner souter h souter l R sinner stotal A h •How is the charge distributed on the cylindrical shell? •What is sinner? •What is souter? B •What is the electric field at r<R? C •What is the electric field for r>R? What is sinner? A1 souter l R sinner stotal h •The electric field inside the cylindrical shell is zero. •Choose as our Gaussian surface a cylinder, which lies inside the cylindrical shell. •Then the net charge enclosed is zero. •Therefore, there will be a surface charge density on the inside wall of the cylinder to balance out the charge along the line. What is sinner? A1 souter l R sinner stotal h •The total charge on the enclosed portion (of length h) of the line charge is l h •Therefore, the charge on the inner surface of the conducting cylindrical shell is Qinner l h •The total charge is evenly distributed along the inside surface of the cylinder. •Therefore, the inner surface charge density sinner is just Qinner divided by total area of the cylinder: •Notice that the result is independent of h. s inner l h l 2 Rh 2 R What is souter? A2 souter l R stotal sinner h •We know that the net charge density on the cylinder is stotal. • The charge densities on the inner and outer surfaces of the cylindrical shell have to add up to stotal. •Therefore, souter =stotal – sinner = stotal +l /(2 R). B What is the Electric Field at r<R? h Gaussian surface l r R h •Whenever we are dealing with electric fields created by symmetric charged surfaces, we must always first chose an appropriate Gaussian surface. •In this case, for r <R, the appropriate surface surrounding the line charge is a cylinder of radius r. B What is the Electric Field at r<R? h Gaussian surface l r R h Using Gauss’ Law, the E field is given by qenclosed 0 lh AE r 2 rhEr 0 qenclosed is the charge on the enclosed line charge lh, (2rh) is the area of the barrel of the Gaussian surface. The Field at radius r is: C What is the Electric field for r>R? Gaussian surface R stotal • • • • • r h Chose a Gaussian surface as indicated above. Charge enclosed in our Gaussian surface •Net charge enclosed on the line: lh •Net charge on the cylindrical shell: = 2Rh stotal Therefore, net charge enclosed is 2 Rhs total + l h The surface area of the Gaussian surface is 2rh Gauss’ Law: 2 Rhs total + l h AEr 2 rhEr 0 •Solve for Er to find l Summary • Practice Gauss’ Law problems • Remember SYMMETRY, CONSTANT FIELD • Choose appropriate Gaussian surface EA qenclosed 0 • Next week Electric Potential. Read Chapter 24 • Try Chapter 23 problems 25, 33, 47, 51, 56 • Next week: Quiz on Thursday and Friday will be on chapters 21,22,23