Download Introduction Introduction to statistical statistical mechanics











Introduction to statistical mechanics
mechanics..
The macroscopic and the microscopic states.
states.
Equilibrium and observation time
time..
Equilibrium and molecular motion
motion..
Relaxation time
time..
Local equilibrium
equilibrium..
Phase space
p
of a classical system
system.
y
.
Statistical ensemble
ensemble..
Liouville’s theorem.
theorem.
Density matrix in statistical mechanics and its
properties..
properties
 Liouville’s
Li
Liouville’sill ’ -Neiman
N i
equation
equation.
ti .
1
Introduction to statistical mechanics.
F
From
th
the seventeenth
t
th century
t
onward
d it was realized
li d th
thatt
material systems could often be described by a small
number of descriptive parameters that were related to
one another in simple lawlike ways.
These parameters referred to geometric,
geometric dynamical and
thermal properties of matter.
Typical
T
i l off the
th laws
l
was the
th ideal
id l gas law
l that
th t related
l t d
product of pressure and volume of a gas to the
temperature of the gas
gas.
2
Bernoulli (1738)
Joule (1851)
Krönig (1856)
Cl
Clausius
i (1857)
C. Maxwell (1860)
L Boltzmann
L.
B lt
(1871)
J. Loschmidt (1876)
H. Poincaré ((1890))
J. Gibbs (1902)
Planck ((1900))
Langevin (1908)
Compton (1923)
Smoluchowski (1906)
Bose (1924)
Debye (1912)
T Ehrenfest
T.
Ei t i (1905)
Einstein
Pauli (1925)
Thomas (1927)
Dirac (1927)
Fermi (1926)
Landau (1927)
3
Energy States
Unstable:
falling or rolling


Stable
M t t bl :
Metastable:
Metastable
in lowlow-energy perch
Figure 5-1. Stability states. Winter (2001) An
Introduction to Igneous and Metamorphic Petrolog
Prentice Hall.
We work with systems which are in equilibrium
How do we define equilibrium
q
?
The system can be in Mechanical, Chemical
and
d Thermal
h
l equilibrium
ilib i
We call all these three together as “Thermodynamic
Equilibrium .
Equilibrium”
Which means : all the energy
gy states are equally
q
y
accessible for all the particles
H
How
d
do we di
distinguish
i
i hb
between Cl
Classical
i l and
d
Quantum systems?
5
Mi
Microscopic
i and
d macroscopic
i states
The main aim of this course is the investigation of general properties of the
macroscopic systems with a large number of degrees of dynamically
freedom (with N ~ 1020 particles for example).
From the mechanical point of view, such systems are very complicated. But
in the usual case only a few physical parameters, say temperature, the
pressure and
d the
th density,
d it are measured,
d by
b means off which
hi h the
th ’’state’’
’’ t t ’’ off
the system is specified.
A state defined in this cruder manner is called a macroscopic state or
thermodynamic state. On the other hand, from a dynamical point of view,
each state of a system can be defined, at least in principle, as precisely as
possible by specifying all of the dynamical variables of the system.
system Such a
state is called a microscopic state.
state
6
Properties of individual molecules
Position
Molecular geometry
Intermolecular forces
Properties of bulk fluid
(
(macroscopic
i properties)
ti )
Pressure
Internal Energy
H t Capacity
Heat
C
it
Entropy
Viscosity
What we know
Solution
S
l ti to
t S
Schrodinger
h di
equation
ti (Eigen-value
(Ei
l
problem)
h2
  2  i2   U  E
 Wave function
i 8 mi
 Allowed energy levels : E
n
Using the molecular partition function, we can
calculate average values of property at given
STATE
QUANTUM STATE.
Quantum states are changing so rapidly that the
observed dynamic properties are actually time
average over quantum states.
Definition and Features the Thermodynamic
y
Method
Thermodynamics is a macroscopic, phenomenological
theoryy of heat.
Basic features of the thermodynamic method:
• Multi-particle physical systems is described by means of a small number of
macroscopically measurable parameters, the thermodynamic parameters: V, P, T, S
(volume, pressure, temperature, entropy), and others.
Note: macroscopic objects contain ~ 1023…1024 atoms (Avogadro’s number ~ 6x1023mol–
1) .
• The connections between thermodynamic parameters are found from the general
laws of thermodynamics.
• The laws of thermodynamics are regarded as experimental facts.
Therefore, thermodynamics is a phenomenological theory.
• Thermodynamics is in fact a theory of equilibrium states, i.e. the states with timeindependent (relaxed) V, P, T and S. Term “dynamics” is understood only in the sense
“how one thermodynamic parameters varies with a change of another parameter in two
successive equilibrium states of the system”.
Classification of Thermodynamic Parameters
Internal and external parameters:
• External parameters can be prescribed by means of external influences on the system by
specifying external boundaries and fields.
• Internal parameters are determined by the state of the system itself for given values of the
external parameters.
Note: the same parameter may appear as external in one system, and as internal in another
system.
Intensive and extensive parameters:
p
• Intensive parameters are independent of the number of particles in the system, and they
serve as general characteristics of the thermal atomic motion (temperature, chemical
potential).
• Extensive parameters are proportional to the total mass or the number of particles in the
system (internal energy,
energy entropy)
entropy).
Note: this classification is invariant with respect to the choice of a system.
Internal and External Parameters: Examples
A same parameter may appear both as external and internal in various systems:
System A
T  Const
System B
M
P
V = Const
External parameter: V
Internal parameter: P
P=
Const
V
External parameter: P, P = Mg/A
Internal parameter: V, V = Ah
State Vector and State Equation
Application of the thermodynamic method implies that the system if found in the state of
thermodynamic equilibrium, denoted X, which is defined by time-invariant state parameters,
such as volume, temperature
p
and p
pressure:
X  (V , T , P )
The parameters (V,T,P)
(V T P) are macroscopically measurable
measurable.
One or two of them may be replaced by non-measurable
parameters, such internal energy or entropy.
Note that only the mean quantity of a state parameter A
is time-invariant, see the plot.
A mathematical relationship that involve a complete set of measurable parameters (V,T,P)
(V T P) is
called the thermodynamic state equation
f (V , T , P,  )  0
Here,
ξ is the vector of system parameters
Averaging
The physical quantities observed in the macroscopic state are the result
of these variables averaging in the warrantable microscopic states. The
statistical hypothesis about the microscopic state distribution is
required for the correct averaging
averaging.
To find the right method of averaging is the fundamental principle of
the statistical method for investigation of macroscopic systems.
The derivation
Th
d i ti off generall physical
h i l lows
l
f
from
th experimental
the
i
t l results
lt
without consideration of the atomic-molecular structure is the main
principle of thermodynamic approach.
13
Averaging Method
Probability of observing particular quantum
state i
ni
Pi 
n
i
i
E
Ensemble
bl average off a d
dynamic
i property
t
 E   Ei Pi
i
Time average and ensemble average
U  lim  Ei ti  lim  Ei Pi
 
n 
i
Thermodynamics and Statistical Mechanics
Probabilities
15
Pair of Dice
For one die, the probability of any face
coming
i up is
i the
th same, 1/6.
1/6 Therefore,
Th f
it
is equally probable that any number from
one to six will come up.
For two dice, what is the probability
that the total will come up 2, 3, 4, etc up
to 12?
16
Probability
To calculate the probability of a
particular
ti l outcome,
t
countt th
the number
b off
all possible results. Then count the
number that give the desired outcome.
The probability of the desired outcome is
equal to the number that gives the
desired outcome divided by the total
number of outcomes. Hence, 1/6 for one
di
die.
17
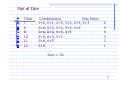
Pair of Dice
List all
dice.
dice
Total
2
3
4
5
6
possible outcomes (36) for a pair of
Combinations
How Many
1+1
1
1+2,, 2+1
2
1+3, 3+1, 2+2
3
1+4 4+1,
4+1 2+3,
2+3 3+2
1+4,
4
1+5, 5+1, 2+4, 4+2, 3+3
5
18
Pair of Dice
Total
7
8
9
10
11
12
Combinations
How Many
1+6 6+1,
1+6,
6+1 2+5,
2+5 5+2,
5+2 3+4,
3+4 4+3
2+6, 6+2, 3+5, 5+3, 4+4
3+6 6+3,
3+6,
6+3 4+5,
4+5 5+4
4+6, 6+4, 5+5
5+6, 6+5
6+6
6
5
4
3
2
1
Sum = 36
19
Probabilities for Two Dice
Total 2
1
Prob.
36
% 2.8
28
3
2
36
56
5.6
4
3
36
83
8.3
5
4
36
11
6
5
36
14
7
6
36
17
8
5
36
14
9 10 11 12
4 3 2 1
36 36 36 36
11 8.3
8 3 5.6
5 6 2.8
28
20
Probabilities for Two Dice
Probab
bility
Dice
0.18
0 16
0.16
0.14
0.12
01
0.1
0.08
0.06
0.04
0 02
0.02
0
2
3
4
5
6
7
8
Number
9
10
11
12
21
Microstates and Macrostates
Each possible outcome is called a
“microstate”.
The combination of all microstates that
give the same number of spots is called a
“macrostate”.
The macrostate that contains the most
microstates is the most probable to occur.
22
Combining
g Probabilities
If a given
i
outcome
t
can b
be reached
h d in
i two
t
(or
(
more) mutually exclusive ways whose
probabilities
b biliti are pA and
d pB, then
th the
th probability
b bilit
of that outcome is: pA + pB.
This is the p
probabilityy of having
g either A or B.
23
Combining Probabilities
If a given outcome represents the
combination of two independent events,
events whose
individual probabilities are pA and pB, then the
probability of that outcome is: pA × pB.
This is the probability of having both A and B.
24
Example
Paint two faces of a die red. When the
di is
die
i thrown,
th
what
h t is
i the
th probability
b bilit off a
red face coming up?
1 1 1
p  
6 6 3
25
Another Example
Throw two normal dice. What is the
probability
b bilit off two
t
sixes
i
coming
i up??
1 1 1
p ( 2)   
6 6 36
26
Complications
p is the p
probabilityy of success. (1/6
( / for
one die)
q is the probability of failure
failure. (5/6 for
one die)
p + q = 1,
or
q=1–p
When two dice are thrown
thrown, what is the
probability of getting only one six?
27
Complications
Probabilityy of the six on the first die and
not the second is:
1 5 5
pq   
6 6 36
Probability of the six on the second die
and not the first is the same
same, so:
10 5
p (1)  2 pq  
36 18
28
Simplification
p
Probability of no sixes coming up is:
5 5 25
p (0)  qq   
6 6 36
The sum of all three probabilities is:
p(2) + p(1) + p(0) = 1
29
Simplification
p(2) + p(1) + p(0) = 1
p² + 2pq + q² =1
(p + q))² = 1
The exponent is the number of dice (or
tries).
Is this general?
30
Three Dice
(p + q)³ = 1
p³ + 3p²q + 3pq² + q³ = 1
p(3) + p(2) + p(1) + p(0) = 1
It works! It must be general!
(p + q)N = 1
31
Binomial Distribution
Probability of n successes in N attempts
(p + q)N = 1
N!
n N n
P ( n) 
p q
n!( N  n)!
where, q = 1 – p.
32
Thermodynamic Probability
The term with all the factorials in the
previous equation is the number of
i
t t th
ill lead
l d to
t the
th particular
ti l
microstates
thatt will
macrostate. It is called the
“thermodynamic probability”, wn.
N!
wn 
n! ( N  n ))!
33
Microstates
The total number of microstates is:
  w
wn
True p
probability P(n) 

For a very large number of
particles
i l
w
max
34
Mean of Binomial Distribution
n   P ( n) n
n
where
N!
n N n
P ( n) 
p q
n!( N  n)!

Notice : p P (n)  P (n)n
p
35
Mean of Binomial Distribution

n   P ( n) n   p P ( n)
p
n
n


N
n  p  P ( n)  p ( p  q )
p n
p
n  pN ( p  q )
N 1
 pN (1)
N 1
n  pN
36
Standard Deviation ()
n  n 

2
  n  n    P(n)n  n 
2
2
2
n
n  n 
2
 n  2n n  n  n  2n n  n
2
2
 n n
2
2
2
2
2
37
Standard Deviation
2
 
n   P ( n) n   p   P ( n)
n
 p  n
    
 
2
N
N 1
n   p  p ( p  q )   p  pN ( p  q )
 p  p 
 p 
2
n  pN ( p  q )
2
2
N 1
p
pN ( N  1)( p  q )
N 2

n 2  pN 1  pN  p   pN q  pN 
38
Standard Deviation
 n n
2
2
2
 2  pN q  pN   ( pN ) 2
  Npq  ( pN )  ( pN )  Npq
  Npq
pq
2
2
2
39
For a Binomial Distribution
n  pN
  Npq

q

Np
p
n
40
Coins
Toss 6 coins. Probabilityy of n heads:
n
6 n
N!
6!
1 1
n N n
P ( n) 
p q

   
n!( N  n)!
n!(6  n)!  2   2 
6!
1
P ( n) 
 
n!(6  n)!  2 
6
41
For Six Coins
Binomial Distribution
0.35
03
0.3
Probab
bilty
0.25
0.2
0.15
0.1
0.05
0
0
1
2
3
Successes
4
5
6
42
For 100 Coins
Binomial Distribution
0.09
0.08
0.06
0.05
0.04
0.03
0.02
0.01
96
90
84
78
72
66
60
54
48
42
36
30
24
18
12
6
0
0
Proba
abilty
0.07
Successes
43
For 1000 Coins
Binomial Distribution
0.03
0.02
0.015
0.01
0.005
960
900
840
780
720
660
600
540
480
420
360
300
240
180
120
60
0
0
Probabilty
0 025
0.025
Successes
44
Multiple
p Outcomes
N!
N!
w

N1! N 2 ! N 3!     N i !
N
i
N
i
45
Stirling’s Approximation
For large N : ln N ! N ln N  N
 N! 
  ln N ! ln  N i !  ln N ! ln N i !
ln w  ln
i
  Ni!


ln w  N ln N  N    ( N i ln N i )   N i 
i
 i

ln w  N ln N   ( N i ln N i )
i
46
Number Expected
T
Toss
6 coins
i N times.
ti
Probability
P b bilit off n heads:
h d
n
6 n
N!
6!
1 1
n N n
P ( n) 
p q

   
n!( N  n)!
n!(6  n)!  2   2 
6
6!
1
P ( n) 
 
n!(6  n)!  2 
N b off ti
d is
i expected
t d is:
i
Number
times n h
heads
n = N P(n)
47
Zero Low of Thermodynamics
One of the main significant points in thermodynamics (some times they
call it the zero low of thermodynamics) is the conclusion that every
enclosure (isolated from others) system in time come into the
equilibrium state where all the physical parameters characterizing the
system are not changing in time. The process of equilibrium setting is
called the relaxation p
process off the system
y
and the time off this p
process
is the relaxation time.
Equilibrium means that the separate parts of the system (subsystems)
are also in the state of internal equilibrium (if one will isolate them
nothing will happen with them). The are also in equilibrium with each
other- no exchange
g byy energy
gy and p
particles between them.
48
Local equilibrium
Local equilibrium means that the system is consist
from the subsystems
subsystems, that by themselves are in the
state of internal equilibrium but there is no any
equilibrium
q
between the subsystems.
y
The number of macroscopic parameters is increasing
with digression of the system from the total
equilibrium
49
Classical phase system
Let (q1, q2 ..... qs) be the generalized coordinates of a system
with i degrees of freedom and (p1 p2..... ps) their conjugate
moment.
t A microscopic
i
i state
t t off the
th system
t
i defined
is
d fi d by
b
specifying the values of (q1, q2 ..... qs, p1 p2..... ps).
The 2s-dimensional space constructed from these 2s variables
as the coordinates in the phase space of the system. Each
point in the phase space (phase point) corresponds to a
microscopic state. Therefore the microscopic states in classical
statistical mechanics make a continuous set of ppoints in pphase
space.
50
Ph
Phase
Space
S
pN
t2
2
t1
1
Phase space
  p1 , p 2 , p 3 ,..., p N , r1 , r1 , r3 ,..., rN 
rN
Phase Orbit
If the Hamiltonian of the system is denoted by H(q,p),
the motion of phase point can be along the phase orbit
and is determined by the canonical equation of motion
H
qi 
 pi
 H
pi  
 qi

P

(i=1 2 s)
(i=1,2....s)
H ( q, p )  E
(1 1)
(1.1)
(1.2)
Phase Orbit
Constant energy surface
H(q,p)=E
Therefore the phase orbit must
lie on a surface of constant
energy (ergodic
ergodic surface
surface).
52
 - space and 
-space
space
Let us define  - space as phase space of one particle (atom or molecule).
molecule)
The macrosystem phase space (-space)
space is equal to the sum of  - spaces
spaces.
The set of possible microstates can be presented by continues set of phase
points. Every point can move by itself along it’s own phase orbit. The
overall picture of this movement possesses certain interesting features,
which are best appreciated in terms of what we call a density function
(q,p;t).
y that at anyy time t, the number of
This function is defined in such a way
representative points in the ’volume element’ (d3Nq d3Np) around the point
(q,p) of the phase space is given by the product (q,p;t) d3Nq d3Np.
Clearly, the density function (q,p;t) symbolizes the manner in which the
members of the ensemble are distributed over various possible microstates
at various instants of time.
53
Function of Statistical Distribution
Let us suppose that the probability of system detection in the volume
ddpdqdp1.... dps dq1..... dqs near point (p,q) equal dw (p,q)= (q,p)d.
The function of statistical distribution  (density function) of the system
over microstates in the case of nonequilibrium systems is also depends on
time. The statistical average of a given dynamical physical quantity f(p,q)
is equal
q 
 f 

f ( p, q )  (q, p; t )d 3 N qd 3 N p
3N
3N

(
q
,
p
;
t
)
d
qd
p

(1.3)
The right
g ’’phase
p
pportrait’’ off the system
y
can be described byy the set off
points distributed in phase space with the density . This number can be
considered as the description of great (number of points) number of
systems each of which has the same structure as the system under
observation copies of such system at particular time, which are by
themselves existing in admissible microstates
54
Statistical Ensemble
The number
Th
b off macroscopically
i ll identical
id ti l systems
t
di t ib t d along
distributed
l
admissible microstates with density  defined as statistical ensemble.
ensemble A
statistical ensembles are defined and named by the distribution function
which characterizes it. The statistical average value have the same
meaning as the ensemble average value.
An ensemble
A
bl is
i said
id to be
b stationary
i
if  does
d
not depend
d
d explicitly
li i l
on time, i.e. at all times

 0
t
(1 4)
(1.4)
Clearly, for such an ensemble the average value <f> of any physical
Clearly
quantity f(p,q) will be independent of time.
time Naturally, then, a stationary
ensemble qualifies to represent a system in equilibrium. To determine the
circumstances
i
under
d which
hi h Eq.
E (1.4)
(1 4) can hold,
h ld we have
h
to make
k a rather
h
study of the movement of the representative points in the phase space.
55
Lioville’s
Lioville
s theorem and its consequences
Consider
C
id an arbitrary
bit
" l
"volume"
"  in
i the
th relevant
l
t region
i off the
th phase
h
space and let the "surface” enclosing this volume increases with time is
given by

t
  d 
(1.5)
where
h
d(d3Nq d3Np)
p).
). On
O the
th other
th hand,
h d the
th nett rate
t att which
hi h the
th
representative points ‘’flow’’ out of the volume  (across the bounding
surface ) is given by

 ρ(ν  n )dσ
(1.6)
σ
here v is the vector of the representative points in the region of the
surface element d, while n̂ is the (outward) unit vector normal to this
element.
l
B the
By
h divergence
di
theorem,
h
(1 6) can be
(1.6)
b written
i
as
56
 div ( v )d
((1.7))
where the operation of divergence means the following:

 


di ( v )    (  qi ) 
div
(  pi )
pi
i 1  qi

3N
(1.8)
In view of the fact that there are no "sources" or "sinks" in the phase
p
space and hence the total number of representative points must be
conserved, we have , by (1.5) and (1.7)


 div( v )d    t   d


or

 
   t  div( v )d  0
t
  d 
(1.9)
(1.10)
57
The necessary and sufficient condition that the volume integral (1.10)
vanish for arbitrary
y volumes  is that the integrated
g
must vanish
everywhere in the relevant region of the phase space. Thus, we must
have

 div (  v )  0
t
(1.11)
which is the equation of continuity for the swarm of the representative
points. This equation means that ensemble of the phase points moving
with time as a flow of liquid without sources or sinks.
Combining (1.8) and (1.11), we obtain

 


div( v )    (  qi ) 
(  pi )
pi
i 1  qi

3N
58




      

q
 

p


i
  
qi 
pi     

0

 t i 1   qi
 pi 
 pi 
i 1   qi


3N
3N
(1 12)
(1.12)
The last group of terms vanishes identically because the equation of
motion, we have for all i,


 qi  H ( qi , pi )  H ( qi , pi )
 p



 qi
 qi  pi
 qi  pi
 pi
2
2
(1.13)
From (1.12), taking into account (1.13) we can easily get the Liouville
equation
 ρ 3N   ρ   ρ    ρ
  
qi 
pi  
 ρ,H   0
 t i 1   qi
 pi   t
(1.14)
where {,H} the Poisson bracket.
59
Further, since (qi,pi;t),
t), the remaining terms in (1.12) may be
combined to give the «total» time derivative of . Thus we finally have
d  

 ,H  0
dt  t
(1.15)
Equation (1.15) embodies the so-called Liouville’s theorem.
According to this theorem (q0,p0;t0)=(q,p;t) or for the equilibrium
system
y
(qq0,pp0)= (q,p),
q p that means the distribution function is the integral
g
of motion. One can formulate the Liouville’s theorem as a principle of
phase volume maintenance.
p
t
t=0
0
q
60
Density
y matrix in statistical mechanics

The microstates in quantum theory will be characterized by a H
(common) Hamiltonian, which may be denoted by the operator. At time
t the physical state of the various systems will be characterized by the
correspondent wave functions (ri,t), where the ri, denote the position
coordinates relevant to the system under study.
study
Let k(ri,t)
t), denote the (normalized) wave function characterizing the
physical state in which the k-th system of the ensemble happens to be at
time t ; naturally, k=1,2....N. The time variation of the function k(t) will
be determined by the Schredinger equation
61

H  k ( t )  i k ( t )
(1.16)
Introducing a complete set of orthonormal functions n, the wave
functions k(t) may be written as
 k (t )   ank (t ) n
(1 17)
(1.17)
ank (t )    n k (t ) d
(1.18)
n
here, n* denotes
h
d
the
h complex
l conjugate
j
off n while
hil d denotes
d
the
h
volume element of the coordinate space of the given system.
Obviously enough,
enough the physical state of the k-th system can be
described equally well in terms of the coefficients . The time variation
of these coefficients will be given by
62
iank (t )  i   n* k (t ) d    n*H  k (t ) d
=
* 
n H 

m

k
am (t ) m d
=  Hnmamk (t )

(1.19)
m
where
H nm    n*H  m d
(1.20)
k
The physical significance of the coefficients a n (t ) is evident from eqn.
((1.17).
) Theyy are the p
probability
y amplitudes
p
for the k-th system
y
of the
ensemble to be in the respective states n; to be practical the number
2
k
a n ( t ) represents the probability that a measurement at time t finds
the k-th system of the ensemble to be in particular state n. Clearly, we
must have
63

2
k
a n (t )
1
(for all k)
(1.21)
n

We now
no introduce
int od e the density
densit operator
ope ato  (t ) as defined by
b the matrix
mat i
elements (density matrix)
1
 mn (t ) 
N
 a
N
k 1
k
m

(t )ank * (t )
(1.22)
clearly, the matrix element mn(t) is the ensemble average of the
quantity am(t)an*(t) which,
which as a rule
rule, varies from member to member in
the ensemble. In particular, the diagonal element mn(t) is the ensemble
average of the probability, a nk ( t ) 2 the latter itself being a (quantummechanical) average.
64
Equation of Motion for the Density Matrix mn(t)
Thus, we are concerned here with a double averaging process - once
due to the probabilistic aspect of the wave functions and again due
to the statistical aspect of the ensemble!!
The quantity mn(t) now represents the probability that a system,
chosen at random from the ensemble,, at time t, is found to be in the
2
state n. In view of (1.21) and (1.22) we have
 ank (t )  1
n
 nn  1
n
 mn (t ) 
1
N
 a
N
k 1
k
m

(t )ank * (t )
(1.23)
Let us determine the equation of motion for the density matrix mn(t
(t).
65
1
i   mn ( t ) 
N
 i a mk ( t ) a nk * ( t )  a mk ( t ) a nk * ( t )
N
k 1

 k*


k
k
* k*
    H ml a l ( t )  a n ( t )  a m ( t )   H nl a l ( t )  
k 1   l

 l

=   H ml  ln ( t )   ml ( t ) H ln 
1
=
N
N
l
= ( H    H ) mn
(1.24)
Here, use has been made of the fact that, in view of the Hermitian
character of the operator, ĤH*nl=Hln. Using the commutator notation,
Eq.(1.24) may be written as
  i  
 H,   0
t 
 
(1.25)
66
This equation Liouville-Neiman is the quantum-mechanical
analogue of the classical equation Liouville.
Some properties of density matrix:
•Density
Density operator is Hermitian, +=

-
•The density operator is normalized
•Diagonal elements of density matrix are non negative
•Represent the probability of physical values
 nn  1
  0
n
67