* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Linear Algebra
Linear least squares (mathematics) wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
Cross product wikipedia , lookup
System of linear equations wikipedia , lookup
Exterior algebra wikipedia , lookup
Rotation matrix wikipedia , lookup
Vector space wikipedia , lookup
Eigenvalues and eigenvectors wikipedia , lookup
Determinant wikipedia , lookup
Jordan normal form wikipedia , lookup
Matrix (mathematics) wikipedia , lookup
Euclidean vector wikipedia , lookup
Principal component analysis wikipedia , lookup
Perron–Frobenius theorem wikipedia , lookup
Non-negative matrix factorization wikipedia , lookup
Orthogonal matrix wikipedia , lookup
Covariance and contravariance of vectors wikipedia , lookup
Cayley–Hamilton theorem wikipedia , lookup
Singular-value decomposition wikipedia , lookup
Gaussian elimination wikipedia , lookup
Four-vector wikipedia , lookup
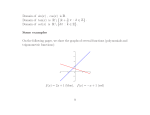
Basics of Linear Algebra A review? Matrix Mathematical term essentially corresponding to an array An arrangement of numbers into rows and columns. Each row is the same length Each column is the same length Usually, we specify a position in the matrix as row, column Vector A one dimensional matrix One row (or one column) We can treat it as a special case of a matrix Matrix operations Matrix (vector) addition/subtraction Add/subtract the corresponding elements in two matrices (vectors) of exactly the same size and shape. 15 17 45 If A = 103 120 115 and B = 210 230 204 32 44 47 301 300 320 62 25 17 What is A + B? Matrices can only be added or subtracted if they are exactly the same size and shape. Multiplication If A is an m x n matrix and B is an n x p matrix, then the product AB is an m x p matrix whose elements are defined by n cij = ∑aikbkj k=1 That is, sum the term by term products of the elements in row I of A column j of B. Transposition If A is m x n, the transpose of A is n x m. The rows become columns and the columns become rows. This is sometimes needed to put things into a form that is compatible for multiplication. Properties The identity matrix has 1s on the main diagonal and 0s elsewhere. Multiplication by the identity matrix yields the original matrix. i.e. AI = IA = A The size of the identity matrix is made to be compatible for the operation intended. The zero matrix has 0 in every position. If A, B, C are of appropriate sizes, then A(BC) = (AB)C A(B+C) = AB +AC (A+B)C = AC + BC Matrix inverse The inverse (A-1) is defined such at A A-1 is I. Not every matrix has an inverse. If no inverse exists, then the matrix is called singular (non invertible) If A is nonsingular, so is A-1 If A, B are nonsingular, then AB is also non singular and (AB) -1 = B -1A -1 (Note reversed order.) If A is nonsingular, then so is its transpose and (AT ) -1 = (A-1)T Vectors and Vector Spaces A vector with 2 elements (a 2-vector) is written x as y The vector is represented by a line in a plane, starting at the origin and ending at the point x,y. For x=2 and y=1: ( ). (2,1) The length of the vector is calculated using the Pythagorean theorem: ||vector|| = √ x2 + y2 Vector operations Addition and subtraction consist of adding or subtracting the corresponding elements. Only vectors of the same size can be added/subtracted. What does the sum of two vectors look like in the coordinate system? Vector angles There is an angle between any two vectors in the coordinate system. One way of comparing the vectors is to measure the angle between them. Cos = x x + y y 1 2 1 2 ||X|| ||Y|| Where ||X|| is the length, or magnitude, of X X= x1 (y ) 1 Y=( x2 y2 ) Dot product and cosine The dot product of vectors X, Y is defined as X * Y = x1x2 + y1y2 So, Cos = X*Y ||X|| ||Y|| If the cosine is 0, the vectors are at right angles. Larger dimensions It is easy to visualize vectors in two space, but larger dimensions are also useful. We cannot draw them so easily, but the properties of length, distance, etc. remain interesting. We can draw 3-vectors. Note that we cannot express the x axis in terms of the y axis. In 3-space, we cannot express any of x, y, z in terms of just the others. The three axes define the space. When we look at the relationships between vectors that define index terms or queries, the relationship between them tells us whether they represent totally unrelated information, or information that is more or less related. Reference for this review: Introductory Linear Algebra with Applications Bernard Kolman Macmillan Publishing, 1984 Chapters 1 and 3.