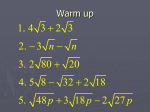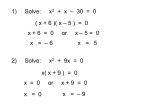* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download simplify radicals
Survey
Document related concepts
Transcript
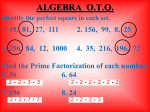
GUIDED NQTES & PRACTICE simplify radicals square & cube roots miss jude MATH! what is a radical? RADICAL EXPRESSIoNS 3 56 24xy 3 5 32 3 1 8 x2 what are perfect squares? 4 81 9 7 x is the inverse of 3 x is the inverse of 4 x is the inverse of 5 x is the inverse of n x is the inverse of 2 3 2 3 16 what are perfect cubes? 42 4 vocabulary we need to know & use decimal approximation: give answer in exact form: simplify a radical Simplifying radicals The square root of a number which is not a __________________ ____________ will be an _________________ number. It is a decimal which does not repeat or terminate. We can estimate a square root by deciding between which two __________________ ________________ it falls. 0 1 2 3 4 5 6 7 8 9 10 12 is between ____ & ____ 2 is between ____ & ____ 82 is between ____ & ____ 20 is between ____ & ____ 8 is between ____ & ____ 56 is between ____ & ____ 29 is between ____ & ____ 1 4 is between ____ & ____ 40 is between ____ & ____ 99 is between ____ & ____ 50 is between ____ & ____ 5 2 is between ____ & ____ write the decimal approximation to each indicated place value square root nearest tenth nearest hundredth nearest thousandth 40 2 66 5 7 3 19 evaluate each root below. If the root does not exist, write DNE. 81 = 400 3 4 81= 16 64= 8 = 8 = = 3 8 = 3 36 + 3 1= 8 1= 2 225 = 1000= 3 125 3 81 = 0.04 = 0.027= 36 - 9= 144 121 3 1 64 = = 900 = 6 49 = 1 64 = 25 = 5 32= 3 100 = 6 49 = 4 0= Simplifying radicals When we need an _____________ _____________ answer, we can’t use a decimal approximation. The best we can do is to ____________________. A fully simplified radical expression has no _________________ _______________ factors. We’ll start with whole numbers. method 1: use the perfects method 2: factor to the primes review perfect square/cube chart. factor out the perfect #. bring the root to the outside. factor completely. circle pairs/triples & bring # to the outside. leave singles. 3 20 200 20 200 48 63 48 63 54 3 -24 3 54 3 -24 simplify each square root or cube root below. 16 10 20 3 3 16 56 72 8 8 18 48 99 98 4 3 64 0.2 75 9 16 81 100 3 250 3 3 288 128 5000 72 24 2 3 54 275 60 8 50 49 16 3 128 6 75 7 72 0.5 3 256 10 162 operations with radicals We can ________ or ____________ the _________ or ___________ by finding the same way we combine like terms. product/quotient of the Add the __________________ of radicals ______________ and ____________ . with the same ________ and _________. Simplify if possible. 3 2 5 2 3 2 5 2 3 75 5 3 2 7 4 12 5 5 8 5 600 96 = 12 72 - 48 108 98 32 10 6 5 3 2 8 4 72 = 20 8 5 3 48 2 10 -5 3 + 2 27= 6 75 12 7 2 5 2 75 7 20 = 2 5 4 5 simplifying radicals with variables we can also simplify radicals with variables in the radicand. we’ll stick to square roots for now and factor by _________ __________. (x)2 (x 2 )2 (x3 )2 (x4 )2 (x5 )2 (x6 )2 x2 x4 x6 x8 x10 x12 what pattern do you notice? ____________________________________________ Perfect squares have _____ exponents. QUICKTIP: ________ the variable exponent by ___ The number __________ the decimal = the exponent of the variable _______ the number _________ the decimal = (0) no variable ___________ = (0.5) variable with power of one _________ to try together…. 49x2 = 200b8 = 12hk3 = 4 50x 5 y 9 = 75m3n4 = 4n7m 243n3m11 = try on your own…. 275h10 3 50xy4 z 96x 7 y 8 98a2b3c4 2 2m4 18m4 = 15x 2 +x 2 1000m8n3 -5 36x 6 y 4 z -3 3w3 3w3 simplifying radicals with variables 125k 3m4 = 121xy6 = 6x 4x 2 = 150y 8 x15 y18 z12 10x 3 8x 6 5x 2 15x 2 2y 2 2x 2 - 3 3v = -2 144x = 4x x8 = 625 -2b 3 320b5 48n9 49x3 = 100 x -1 25x6 = -16 9x 4 10x - 16x2 25 x 169x 3 = -3w3 9w 9 10 16 x 50xy 4 z 2xy 2 z