Download Simple population modeling in a spreadsheet

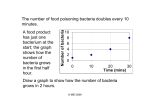
ENGR 213
April 2, 2014
Simple population modeling in a spreadsheet
Background
Bacterial growth depends primarily on two factors – food and space. When bacteria have
plenty of food (ie, growth medium) they will thrive and reproduce by binary fission (or possibly
budding). Binary fission is the process where a mother cell splits into two daughter cells.
(Budding produces only one daughter but the mother cell remains intact.)
Binary Fission - 1: The bacterium before binary fssion has the DNA tightly coiled. 2:
The DNA of the bacterium has replicated. 3: The DNA is pulled to the separate poles of
the bacterium as it increases size to prepare for splitting.(This is missing the fact that
the DNA attaches itself to the inner cell wall) Ergo Diagram not completely correct! 4:
The growth of a new cell wall begins the separation of the bacterium. 5: The new cell
wall fully develops, presenting in the development of downsyndrome, resulting in the
complete split of the bacterium. 6: The new daughter cells have tightly coiled DNA,
ribosomes, and plasmids. (Source: Wikipedia)
If you leave a single bacterium in growth medium overnight, you will find several bacteria
floating around the next day. Or you may possibly find a great many bacteria. This depends
on how often the bacteria reproduce. Some may reproduce as often as an average of once
every 20 minutes! For our purposes, let's say that a particular type of bacterium which we will
study reproduces on average once every 2 hours. If we start with 5 bacteria noon, there will
be 10 bacteria at 2 pm and 20 bacteria at 4 pm.
Mathematically, we express this as a growth rate. The increase in bacteria over time is a
function of the number of bacteria. Each bacterium produces one new bacterium every 2
hours (on average). This defines the reproduction rate constant, k:
new bacteria
1.0
(
old bacteria )
=0.5 /hr
k=
2hours
To find the change in the number of bacteria over time, we can define a differential equation:
ENGR 213
April 2, 2014
dx
=k x
dt
This states that the number of bacteria, x , will increase at a rate of kx (which has units of
bacteria/hr) as a result of reproduction.
The second factor affecting bacterial population is death due to overcrowding. The more
bacteria you have in a small petri dish, the less nutrients will be available for each and the
more waste products will pollute their environment. Some bacteria will not survive an
overcrowded space.
These factors can be accounted for by multiplying the growth rate with a probability of
survival.
(
dx
x
=kx 1−
dt
xmax
)
We will use this equation of bacterial population change for the remainder of this discussion
and for the homework assignment.
To track the changes in bacterial population over time, you can use the Euler method. In
short, this method calculates the value of x at each point in time as a function of the derivative
equation and the value of x at a previous point in time.
x(t +Δ t)=x(t)+ Δt
dx
dt
In this equation, the derivative, dx/dt is evaluated at the previous time, t. There is a more
detailed discussion and an exmaple of the Euler method at the end of these notes.
Here's an example. Let k=0.5 /hr, x max =1 million bacteria, and the initial population of
bacteria is x=0.5 million bacteria. Using an Euler method time step of ∆t=1 hr, we can
calculate the following sequence of population growth.
Time
Population (x, millions)
noon
0.5
1 pm
0.5+(1)*(0.125) = 0.625
2 pm
0.625+1*0.11719 = 0.74219
3 pm
dx / dt =kx (1−x/ xmax )
0.5*0.5*(1-0.5/1) = 0.125
0.5*0.625*(1-0.625/1) = 0.11719
0.5*0.74219*(1-0.74219/1) = 0.09567
0.74219+1*0.09567 = 0.83786 0.5*0.83786*(1-0.83786/1) = 0.06793
ENGR 213
April 2, 2014
Thus, at the end of 3 hours, there will be roughly 0.84 million bacteria in the Petri dish. If you
were to continue this process until midnight, you should see the population grow as shown in
this chart:
Bacterial population (millions)
1.2
1
0.8
0.6
0.4
12:00 PM
03:00 PM
06:00 PM
09:00 PM
Time
For the homework this week, your task is to:
a) Develop a spreadsheet model that calculates the bacterial population of a petri dish over a
period of 12 hours. Use k=0.5 /hr, xmax =1.0 million, ∆ t=1 hr, and the initial value x(0)=0.5
million bacteria in your model. Use the example calculations above to verify your work.
b) Insert a chart into your spreadsheet that plots the bacterial population over the 12 hour
period. The model and chart should be placed on Sheet 1 of the spreadsheet. (The sheets
are identified by tabs on the lower left corner of the window. If you double click on the tab
name, you can change this name to make it more descriptive.) Change the name of “Sheet
1” to “Bacterial growth model”.
c) Copy your model and chart on this first tab and paste it into the tab labeled Sheet 2.
change the name of this sheet to “Alternative model”.
d) Modify the model to use a value of k = 0.3/hr and an initial value of 2.0 million bacteria.
This may involve changing the formulas in the derivative column to reflect the new value of k.
d) Save your spreadsheet in Excel format (.xls or .xlsx) using a filename in this format:
lastname_firstname_HW1.xls. Turn in a copy of your work through the assignment on
PolyLearn in the ENGR 213 course. This assignment is due next week. Late assignments
will be penalized 10%. No assignments will be accepted more than one week late without
permission.
Unless stated otherwise, you may work with others in the class to complete all assignments in
this course. If you do work with others, please be sure to hand in your own work and to
indicate clearly on the assignment who you worked with.
ENGR 213
April 2, 2014
Notes on using spreadsheets
If you are not familiar with working in spreadsheets, there is a detailed example in the
sections below that takes you step by step through solving a problem using the Euler method
using a spreadsheet.
ENGR 213
April 2, 2014
Forward Euler Method
Let's consider a simple rate equation describing the rate of change of some measurable quantity h:
dh
=a h n
dt
The variable h is obviously a function of time (since we can take a derivative with respect to time
dh/dt). So, our notation above implies that there is some function h(t) which desribes how the variable
h changes over time. We can calculate the evolving solution to this rate equation by using Euler's
approximation of the first derivative:
d
h t t  – h t 
h t =
dt
t
h t t – h t 
=a h t  n
t
n
h t t =h t  t a h t 
This numerical approximation is stable and accurate as long as  t is small relative to the time scale of
the changes in h(t).
An initial value of h, h(t=0), is required to begin the solution technique. Let's say this value of h at t=0
is h0. Using this value, each successive value of h can be calculated by taking a small time step,
calculating the rate of change of h, and then incrementing the initial value of h by the product of the
time step and the rate of change.
h0=h0
h t =h0 t ah n0
h2 t=h t t ah  tn
h3  t=h 2 t  t a h 2 t  n
etc.
Sample problem
Use the Euler integration technique to calculate the velocity (meters/sec) at t = 3 seconds for
a rocket launched vertically upwards. You may assume that v = 0 at t = 0 and you should use
∆t = 1 second. The velocity is governed by the following differential equation:
dv
2
=20 – 0.01 v
dt
ENGR 213
April 2, 2014
Solution:
Time (s)
v(t)
0
1
2
3
0
= 0+(1)*(20) = 20
= 20+(1)*(16) = 36
= 36+(1)*(7.04) = 43.04
dv (t)
Notes
dt
= 20 – 0.01*(0) = 20
Given v(0) = 0, calculate dv(0)/dt
= 20 – 0.01*(20^2) = 16 v(1) = v(0)+dt*dv(0)/dt
= 20-0.01*(36^2) = 7.04
= 20–0.01*(43.04^2) = 1.48
Answer: The velocity at t = 3 secs is 43.04 meters/sec
Now let's see how to do this same problem in a spreadsheet program (like MS Office Excel or Open
Office Calc):
1) Create a spreadsheet template that looks like the following:
2) Now, we'll add in the time column from 1 to 5 seconds using a formula. The time should increase in
each box according to the time step, or ∆t, defined in the problem statement. For this problem, ∆t = 1
second. So, each time value is equal to the one above it + 1 second (or +∆t if the time step is not equal
to 1 sec). Cell A2 has a value of 0. Cell A3 should be equal to the value in A2 + 1. To enter this into
cell A3, click on cell A3 and then type: '=A2+1' (without the quotes) and then hit the enter key.
Instead of typing 'A2' you can also use your mouse to click cell A2 and it will be entered in the formula
automatically.
ENGR 213
April 2, 2014
3) After you hit the enter key, the spreadsheet will do the calculation for you and the value '1' will be in
the cell A3 where you typed the formula. While you are at it, save the file to make sure you don't lose
your work!
4) Now you want to copy this formula to the cells below. This will copy the formula which adds 1 to
the value of the cell above the current cell. To do this, click on cell A3. You will see a box on the
lower right corner of the box outline. Click (and hold) on this little box with the mouse and then drag
your mouse down to copy the formula to each of the cells below. Release the mouse button to
complete the action. After you release the mouse button, you should see the values in boxes A4
through A7 have been updated and calculated to contain time values for 2-5 seconds.
This is the little white box
that you click and hold.
5. Now, enter the formula for the derivative dv/dt. Select cell C2 and enter the following formula
(without the quotes): '=20-0.001*(B2)^2'
This formula uses '*' to indicate multiplication and '^2' to indicate that the quantity in the parenthesis
should be squared. The quantity in the parentheses is B2 which holds the value for v at this time (t=0).
After hitting the enter key, the value in C2 is calculated and should be equal to 20.
ENGR 213
April 2, 2014
6) There is one formula left to enter, the Euler approximation for v(t+∆t). We'll enter this in cell B3 to
update the value of v at time t=1. The formula should be: '=B2+(1)*C2'
In this formula, B2 is the value of v(t), the 1 in the parentheses is the value of ∆t, and C2 is the value of
dv/dt at time t. After hitting the enter key, the value of cell B3 will be calculated and should be 20.
7) Now, you will copy the formula in cell B3 to each of the cells below it down to B7 using the click
and drag method from step 4.
8) And, copy the formulas for the derivative, dv/dt, from C2 down to C7.
ENGR 213
April 2, 2014
9) After this you are essentially finished. The problem originally asked for a value of v at 3 seconds.
Your results show that this is 43.04 just as we calculated in the table above. For longer time spans you
will certainly want to use a spreadsheet or some other computer-based solution method. This will
allow you to analyze or graph the results over a period of time. As you see below, we can easily add a
chart (x-y scatter chart) to the spreadsheet to show the trend over time is more or less exponential and
approaches an asymptotic value of approximately 45.
If you are not familiar with inserting a chart, here are some instructions off the MS Excel web page:
Create a Scatter or Line chart
1. Arrange your data so that the x-values are in the first row or column of your
worksheet, and the y-values are located in adjacent rows or columns.
2. Select the range of x- and y-values that you want to plot in the chart.
3. Click Chart on the Insert menu to start the Chart Wizard.
ENGR 213
April 2, 2014
4. In the Chart type box, select XY (Scatter) or Line.
5. Under Chart sub-type, click the chart sub-type you want to use.
For a quick preview of the chart you are creating, click Press and Hold to View Sample.
6. Click Next, and continue with steps 2 through 4 of the Chart Wizard.
Steady state analysis
The asymptotic limit in the example above is also known as the steady state or equilibrium value of the
variable v. The equilibrium value, v∞, is one or more values of a function at which it will no longer
change over time. By definition, this means that the time derivative is equal to zero when v = v∞.
Using the velocity problem from the previous section:
dv
2
=20−0.01 v
dt
At equilibrium, we know the time derivative is equal to zero and v = v∞:
0=20 – 0.01 v ∞2
Solving for v∞:
v ∞2=2000
or
v ∞=±√ 2000=±44.721
In our simple rocket system, the terminal upward velocity is equal to 44.721 m/s. The equilibrum value
of -44.721 (a downward velocity) seems unlikely and in fact it is very unlikely to ever occur. However,
it is at least theoretically a possible steady state solution to the rocket system.
You can check the compatibility of our analysis and the Euler method solution to the rocket problem by
carrying the calculation out for a few more time steps. If you do so, you should find that v = 44.721
m/s at t=7 secs.