Download Logistic regression in SPSS

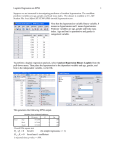
GRA 5917: Input Politics and Public Opinion
Panel data regression in political economy
Lars C. Monkerud, Department of Public Governance,
BI Norwegian School of Management
GRA 5917 Public Opinion and Input Politics. Lecture September 16h 2010
First, though: A short note on logistic regression (from last
week)…
• L (the log-odds, the logit) theoretically varies
between ∞ and - ∞, but P (reasonably) stays within
the 0-1 range:
e e
L
 P 
log

 1 P 
P

1 P

eL
P
1  eL
i.e. the odds of
”success” vs.
”failure”; eb is the
odds-ratio (OR)
Logistic regression
• Intuitively appealing since P=f(Xk) increases in L
as factor Xk changes, but slowly initially and as P
approaches 1:
1
0.9
0.8
0.7
0.6
P
0.5
0.4
0.3
0.2
0.1
0
L(X)
Logistic regression
• Extensions and special variants of the logit
model:
 Pi  n 
  b 0i   b ki X k  
Logit i  Li  log 
 Pi n 
 cn

  Pi 
Logit c  L c  log  i c1n   b 0c   b k X k  


 1   Pi 
i 1


the multinomial logit model, which
models responses in i=1 to n categories
(with i=n the reference category)
the ordinal logit model, which models
responses in i=1 to n ordered
categories (with i=n the reference
category), assuming that the oddsratio effect on the odds of a lower
ordered event (i.e. numerator events
vs. denominator events) is
independent of the observed category
response (aka the proportional odds
model)
Logistic regression in SPSS
Choose Analyze >
Generalized Linear
Models
Logistic regression in SPSS
A flexible tool with
many possible
model specifications
Choose Binary
logistic
Logistic regression in SPSS
Choose dependent
variable
Choose reference
category, i.e. to
model P(not in ref.
category)
Logistic regression in SPSS
Choose predictors:
class variables
(factors) or
contiuous variables
(covariates)
Logistic regression in SPSS
Build model
Presenting changes in P(y=1) from logistic regression
results
Have estimated L=0.4+1.2·X for X ranging from -4 to 10
Presenting changes in P(y=1) from logistic regression
results
Have estimated L=0.4+1.2·X for X ranging from -4 to 10
Excercises (I)
a)
You are interested in how people’s age influences their general feeling of happiness.
Use the XWVSEVS_1981_2000_v20060423.sav data set supplied under the PolEc
Dataset folder on It’s Learning.
a)
Create a new variable happy that takes on the value 1 if the individual in
question reports to be happy (’very’ or ’quite’) and 0 otherwise. Run a simple
binary logistic regression with happy as dependent variable and (continous) age
(x003) and the indivual’s houshold income (x047) as independent variables.
Comment on the results and graph the realtionship between the probability of
being happy and age (Tip: Use descriptive analysis to find the minimum and
maximum of age, i.e. the range for which reasonable predictions of happiness
can be made, and graph the relationship holding income level constant at the
mean).
b)
Redo the analysis with year of birth (x003) added to the model. Comment on the
results in the SPSS output and again graph the relationship between age and the
probability of being happy (holding both year of birth and income cosntant at
their respective means).
Analysis of panel data
A time-invariant covariate…
• Given the correct model…
yit  b 0  b A X Ait  b B X Bi  eit
…estimating the model
N 1
yit  b 0  b A X Ait   D  eit
k
k 1
k
i
will give unbiased estimates of bA: the Dk exhaust varaiation between
cross–section units (i); i.e. influence from all observable and
unobservable time-invariant variables are accounted for
Analysis of panel data in SPSS (I)
OLS regression with country specific (and time specific) dummy variables added to
the equation (as independent variables) with Analyze > Regression > Linear…
problem: How create a large set of dummy variables?
1) Recode group variable
2) Create dummies with syntax, e.g.:
Auto-recode the variable
indexing the groups (e.g.
individuals, countries by proper
names) into a running numeric
code (Transform > Automatic
Recode…)
DO REPEAT d=c1 to c60
/i=1 to 60.
* here, d defines the array of dummy variables
that will be generated (c1, c2 to c60); The i
controls the number of repeats.
COMPUTE d=(cc=i).
* computes the ith element in d (conveniently
named ci) as 1 if cc=i, as 0 otherwise.
END REPEAT.
EXECUTE.
Analysis of panel data in SPSS (II)
Or use the mixed models feature: Analyze > Mixed Models > Linear…
(Maximum Likelihood estimation); creates group dummies from class
variables automatically
Analysis of panel data in SPSS (II)
Click Continue
Analysis of panel data in SPSS (II)
Move the
dependent
variable into
Dependent frame
and class
independents into
Factor(s) and
continuous
independents into
Covariate(s);
choose REML
estimation under
Estimation… and
Parameter
Estimates under
Statistics…
Analysis of panel data in SPSS (II)
Click Fixed…
Analysis of panel data in SPSS (II)
Mark variables
that will appear in
the Factors and
Covariates frame
and Add them to
the Model frame.
Click Continue
Analysis of panel data in SPSS (II)
Click OK to start
analysis
A note on within R2
In the output from the mixed… procedure we get estimates of residuals:
The often reported measure of within R2 is simply:
(Residual Model with group effects only – Residual Full Model)/ Residual Model with group effects only
i.e. the proprortion of explainable variance (after group effects have been taken into
account) that is explained by variables varying within groups
Analysis of panel data (II)…
• Instead of the model…
N 1
yit  b 0  b A X Ait   D  eit
k
k 1
k
i
…one could estimate the random effects model
yit  b 0  b A X Ait  b B X Bi  vi  eit
Valid if the group effect vi (viewed as a disturbance term) is
uncorrelated with other regressors… (and RE estimator of bA will be
more efficient than the FE estimator)
Analysis of panel data in SPSS (II)
Click Random
and build random
terms in same
way as you would
build fixed terms
Excercises (II)
a)
Use the 60panel…sav set supplied under today’s lecture.
a)
Redo the P&T’s analysis in model (1) in table 3.2 (Persson and Tabellini
2005:44). Compare the results with those presented in the book.
b)
Redo the P&T’s analysis in model (2) and (3) in table 3.2 (Persson and Tabellini
2005:44). (Tip: Before analysis, use select cases using the criteria discussed on
pp. 76-77 in P&T).