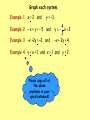* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Graphing A Linear Inequality
Survey
Document related concepts
Transcript
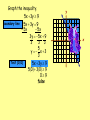
6-8 Systems of Linear Inequalities Select 2 colored pencils that blend together to produce a third distinct color! Algebra 1 Glencoe McGraw-Hill Linda Stamper Systems of Linear Inequalities Two or more linear inequalities in the same variables form a system of linear inequalities. A solution of a system of linear inequalities in two variables is an ordered pair that is a solution of each inequality in the system. When graphing a system of linear inequalities, graph each inequality in the same coordinate plane. Do you remember how to graph an inequality? Graphing A Linear Inequality The graph of a linear inequality in two variables is the graph of the solutions of the inequality. A boundary line divides the coordinate plane into two half-planes. The solution of a linear inequality in two variables is a half-plane. Shade the side of the half-plane that contains the solutions. y x Graphing A Linear Inequality The graph of a linear inequality in two variables is the graph of the solutions of the inequality. A boundary line divides the coordinate plane into two half-planes. The solution of a linear inequality in two variables is a half-plane. Shade the side of the half-plane that contains the solutions. y x Graphing A Linear Inequality Use a dashed boundary line for < or >. A dashed line indicates that the points on the line are NOT solutions. Use a solid boundary line for < or >. A solid line indicates that the points on the line are solutions. y x Graphing A Linear Inequality 1. Graph the corresponding equation, using a dashed (< or >) line or a solid ( < or >) line. You may need to write the equation in slope-intercept form to graph the boundary line. 2. Test the coordinates of a point in one of the half-planes. You can use any point that is not on the line as a test point. 3. Shade the half-plane containing the test point if it is a solution of the inequality. If it is not a solution, shade the other half-plane. Graph the inequality. 5x 3y 9 boundary line 5x 3y 9 5x 5x 3y 5x 9 3 3 3 5 y x 3 3 Test (0,0) 5x 3y 9 50 30 9 09 false y • • • x Graph the system x < 1 and y > 2. Write one inequality. Write the related equation. Graph the equation; solid boundary line. Test a point. Use (0,0) if possible. x<1 x 1 x 1 0 1 true y • x Use the y 2 Test is true, so shade inequality y 2 half-plane that does to test the dashed boundary line The overlap It is not a contain thethe test point. point! Would Test (0,0) represents the solution ordered pair Test false – shade halfRepeat above steps to solution of the because it (1,2) be a plane that does not graph the other system. That is the must be true solution of contain of thethe test point. inequality on the same intersection for both the system? coordinate plane. two inequalities! inequalities! Graph each system. Example 1 x > 2 and y > –3. Example 2 – x + y > – 5 and Example 3 –x +2y > –2 and 4 y x 2. 3 –x + 2y < 4. Example 4 y < x + 1 and x > 1 and y > 2. Please copy all of the above problems in your spiral notebook! Example 1 Graph the system x > 2 and y > –3. x>2 x 2 x2 02 false y 3 y 3 dashed boundary line 0 3 true Use the inequality to test the point! y • The solution is the intersection of the two inequalities! x 4 3 Example 2 Graph the system – x + y > – 5 and y x 2. x y 5 x y 5 y x 5 Test (0,0) in original inequality. Test true – shade half-plane that contains test point. 4 y x 2 3 4 y x 2 3 Test (0,0) in original inequality. Test true – shade half-plane that contains test point. y • • • The solution is the intersection of the two inequalities! • x Example 3 Graph the system –x +2y > –2 and –x + 2y < 4. x 2y 4 x 2y 2 x 2y 4 x 2y 2 2y x 2 2y x 4 1 1 y x 1 y x 2 2 2 Test (0,0) in Test (0,0) in original inequality. original inequality. y • • • • Test true – shade Test true – shade half-plane that half-plane that contains test point. contains test point. The solution is the intersection of the two inequalities! x Example 4 Graph the system y < x + 1 and x > 1 and y > 2. y x 1 y x 1 • • y x Example 4 Graph the system y < x + 1 and x > 1 and y > 2. y x 1 y x 1 x 1 x 1 y 2 y 2 • • y Note the region that is the intersection of these two inequalities! The intersection of all 3 inequalities represents the solution of the system. x 6-A14 Pages 343-345 # 7–18, 37, 47-50.