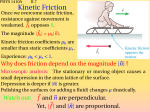
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Essential Physics Activities on a Budget Price
Center of mass wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Classical central-force problem wikipedia , lookup
Matter wave wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Surface wave inversion wikipedia , lookup
Faster-than-light wikipedia , lookup
Variable speed of light wikipedia , lookup
Essential Physics Activities on a Budget Price Low Cost Physics Activities Center for Mathematics and Science Education Texas A&M University - College Station (Note: This web page was constructed using Microsoft FrontPage 2002 and is best viewed using Internet Explorer) Physics experiments/activities do not have to be costly in time or resources. Teachers also do not need to limit their equipment purchases to "high tech" or specialty materials sold exclusively through science supply catalogs. Many valuable data collection activities can be performed using inexpensive materials that may be purchased from local department, hardware, and/or toy stores. The activities contained in the chart below represent a few of what I personally consider the "best for the buck" when it comes to introductory physics' essential laboratory activities on a tight budget. I have used all of them in high school and/or introductory undergraduate physics courses. Activities similar to these using a variety of materials may be found in numerous lab resource materials. The purpose of this web page is not to introduce new and/or unique lab activities, but to present some of the most common and valuable lab experiences involving real data collection in a format for use with inexpensive materials. Activity worksheet documents are presented in both PDF and Microsoft Word format so that they may be easily downloaded, printed, and/or modified according to the individual needs of each user. http://www.science.tamu.edu/CMSE/LowCostPhysicsActivities.htm (1 of 6) [8/21/2004 2:05:37 PM] Essential Physics Activities on a Budget Price Click on a MS Word or PDF "Worksheet Link" to download an experiment/activity worksheet. Click on the "To the Teacher" link to view suggestions and information regarding the activity, materials, and approximate costs. "Other Links" provides links to other web pages with activities/information/simulations related to the chosen physics topic (all links active as of 3/9/2004). Activity Worksheet Link To the Teacher Other Links 1 Precision of Lab Equipment MS Word, PDF link link1 link2 link3 2 Constant and Relative Velocity MS Word, PDF link link1 link2 link3 3 Motion Graphs (Virtual Activity) MS Word, PDF link link1 link2 link3 4 Accelerated Motion MS Word, PDF link link1 link2 link3 5 Free Fall (Virtual Activity) MS Word, PDF link link1 link2 link3 6 Resultant Vectors MS Word, PDF link link1 link2 link3 7 Softball Throw MS Word, PDF link link1 link2 link3 8 Newton's 2nd Law (Virtual Activity 1) MS Word, PDF link link1 link2 link3 9 Newton's 2nd Law (Virtual Activity 2) MS Word, PDF link link1 link2 link3 http://www.science.tamu.edu/CMSE/LowCostPhysicsActivities.htm (2 of 6) [8/21/2004 2:05:37 PM] Essential Physics Activities on a Budget Price 10 The Pendulum MS Word, PDF link link1 link2 link3 11 Sliding Friction MS Word, PDF link link1 link2 link3 12 Forces in Equilibrium MS Word, PDF link link1 link2 link3 13 Work and the Inclined Plane MS Word, PDF link link1 link2 link3 14 One-Dimensional Collisions (Virtual Activity) MS Word, PDF link link1, link2, link3 15 Two-Dimensional Collisions (Virtual Activity) MS Word, PDF link link1, link2, link3 16 Torque and Rotational Equilibrium MS Word, PDF link link1 link2 link3 link link1 link2 link3 17 Power MS Word, PDF 18 Wave Modeling MS Word, PDF link link1 link2 link3 19 "Slinky" Waves MS Word, PDF link link1 link2 link3 20 Ripple Tank (Virtual Activity) MS Word, PDF link link1 link2 link3 21 Resonance: Speed of Sound MS Word, PDF link link1 link2 link3 MS Word, PDF link link1 link2 link3 PowerPoint Slide link link1 link2 link3 22 23 Palm Pipes and Chimes Reflection in Plane Mirrors http://www.science.tamu.edu/CMSE/LowCostPhysicsActivities.htm (3 of 6) [8/21/2004 2:05:37 PM] Essential Physics Activities on a Budget Price 24 Full Length Mirrors MS Word, PDF link link1 link2 link3 25 Curved Mirror Diagrams MS Word, PDF link link1 link2 link3 26 Index of Refraction MS Word, PDF link link1 link2 link3 27 Lens Diagrams MS Word, PDF link link1 link2 link3 MS Word, PDF link link1 link2 link3 MS Word, PDF link link1, link2, link3 MS Word, PDF link link1 link2 link3 28 29 30 Images in Converging Lenses Color Electrical Circuits and Conductivity 31 Ohm's Law MS Word, PDF link link1 link2 link3 32 Light Bulb Circuits MS Word, PDF link link1 link2 link3 33 Electrical Energy Costs MS Word, PDF link link1, link2, link3 34 Electromagnets MS Word, PDF link link1 link2 link3 35 Electric Motors MS Word, PDF link link1 link2 link3 MS Word, PDF link link1 link2 link3 36 Simulated Radioactive Decay http://www.science.tamu.edu/CMSE/LowCostPhysicsActivities.htm (4 of 6) [8/21/2004 2:05:37 PM] Essential Physics Activities on a Budget Price Recently developed video analysis technology offers an exciting and relatively inexpensive way to analyze many types of one and two-dimensional motion. Go to http://www.science.tamu.edu/CMSE/videoanalysis/index.htm to learn more about some of the currently available video analysis programs, including one free program that may be downloaded from an internet site linked to the page. Also linked to this site are 19 video clips of many types of motion commonly studied in introductory physics and physical science courses and suggestions for their use. The 36 activities linked to this page and the 19 video analysis activities provide an excellent way for an entire introductory level physics class to include 55 laboratory activities at an unbelievably low cost. In addition to these activities and web site links, physics teachers of all levels may be interested in the following web sites offering tutorials, downloadable software, etc... : Name Description URL Link Graph Paper Create numerous types of custom graph paper Printer Program link The Diagnoser Project A web-based assessment program that serves as a formative diagnostic of student content knowledge link MERLOT A search engine for science web sites link NetLogo A modeling program useful for many science areas link Journal of Online journal directly related to issues in physics Physics Teacher teaching and the preparation of physics teachers Education Online link Singing Science "Cheesy" science songs from the 1950s and 1960s Records link Physics 2000 Very comprehensive tutorial program link The Physics Classroom Very comprehensive tutorial program link http://www.science.tamu.edu/CMSE/LowCostPhysicsActivities.htm (5 of 6) [8/21/2004 2:05:37 PM] Essential Physics Activities on a Budget Price Conceptual Physics SURF Informative site supplementing Paul Hewitt's Conceptual Physics textbook link For more information or comments about this web page or its activities, to suggest other activities, or to request a workshop or professional development session demonstrating the use of the activities, please contact: Joel A. Bryan, Ph.D. [email protected] (979) 458-0604 Center for Mathematics and Science Education Texas A&M University - Mail Stop 4232 College Station, TX 77843-4232 http://www.science.tamu.edu/CMSE/LowCostPhysicsActivities.htm (6 of 6) [8/21/2004 2:05:37 PM] CMSE Phys Precision of Lab Measurements Triple Beam Balance Record the mass, in grams, of three (3) common objects using the triple beam balance. Object Mass, g When using this triple beam balance to find mass, you should record your values to the nearest ______________ of a gram because __________________________________________ _______________________________________________________________________. Spring Scale Record the weight, in Newtons, of three (3) common objects using the spring scale. Object Weight, N When using this spring scale to find weight, you should record your values to the nearest _________________ of a Newton because _____________________________________ _______________________________________________________________________. Meter Stick Record the length of three (3) common objects using the meter stick. Object Length, cm When using this meter stick to measure length, you should record your values to the nearest _____________ of a centimeter because _________________________ _______________________________________________________________. Write a letter to a person of your choice in which you explain the rules for recording volume values using as examples 3 beakers that are graduated in ones, in tens, and in hundreds of milliliters (mL). Include a sketch of each type beaker in your letter. CMSE Phys Constant Velocity (Speed) Objective: Measure distance and time during constant velocity (speed) movement. Calculate average velocity (speed) as the slope of a “Position vs. Time” graph. Equipment: battery operated vehicles, stopwatch, meter stick or measuring tape Procedure: 1. Complete the table by timing each vehicle as it travels the indicated distance. 2. Perform two time trials for each distance and take the average value as your accepted time. 3. Use the distances traveled and average time s to make a “Distance vs. Time” graph (always named as “y vs. x”) using MS Excel. Label this and all graphs as directed in class. 4. Use the MS Excel “Add Trendline” function to draw the best straight lines through your data points and to compute the “best fit” equations for the lines. 5. Record the equation for each line on the graph. The slope of each line, given with the units associated with the y- and x-axes, is the average velocity (speed) of each vehicle. Use this information to write the speed of each vehicle on the graphs next to each line. 6. Print your graph or graphs. Distance, meters 0 0.5 1.0 1.5 2.0 2.5 3.0 1 0 Vehicle I Vehicle II Time Trials, seconds Time Trials, seconds 2 0 AVG. 0 1 0 2 0 AVG. 0 Questions: 1. Did each vehicle appear to maintain a constant velocity (speed)? _____ How can you tell by looking at a “position vs. time” graph if the velocity (speed) is constant? 2. How should the “position vs. time” graph of a faster car compare with the graph of a slower car? 1 CMSE Phys Relative Velocity (Speed) In this portion of the lab, you will determine the relative velocity (speed) of your two vehicles as they 1) approach each other from opposite directions, and 2) as the faster vehicle approaches and catches up to the slower one from behind. 1) Based on the average speeds of the two vehicles that you determined in Part I, what do you expect the relative speed of the vehicles to be as they approach each other from opposite directions? (i.e., At what rate should they close in on each other?) _______ Why? 2) What do you expect the relative speed to be as the faster vehicle catches up to the other one from behind? (i.e., At what rate does the faster one close in on the other?) _______ Why? Relative Velocity (Speed) Approaching from Opposite Directions Procedure: 1. Place the vehicles facing each other the distance apart indicated in the table. 2. Turn on each vehicle, releasing them at the same instant. Record the time for the vehicles to meet. Perform two trials and take the average value as your accepted time. 3. Make a graph of “Closing Distance vs. Time” for this procedure. Determine the equation of the line that best fits these data points. The slope of this line will be the relative velocity (speed) of the two vehicles as they approach each other from opposite directions. Closing Distance, m 0.0 0.5 1.0 1.5 2.0 2.5 3.0 Time, seconds Trial 1 0 Trial 2 0 Average Time, seconds 0 2 CMSE Phys Relative Velocity (Speed) as Vehicle Approaches from Behind Procedure continued: 4. Now place the vehicles facing the same direction the distance apart indicated in the table. The faster vehicle should be the indicated distance behind the slower one. 5. Turn on each vehicle, releasing them at the same instant. Record the time for the faster vehicle to catch up to the slower one. Perform two trials and take the average value as your accepted time. 6. Make a graph of “Closing Distance vs. Time” for this procedure. Determine the equation of the best fit line for these data points. The slope of this line will be the relative velocity (speed) of the two cars as the faster vehicle approaches the slower one from behind. Closing Distance, m 0.0 0.20 0.40 0.60 0.80 1.00 1.20 Time, seconds Trial 1 0 Trial 2 0 Time, seconds 0 Questions: 1. Compare your experimental relative speeds with the estimates you made earlier. 2. Do you think your method of calculating relative speeds (addition or subtraction of speeds) is always valid regardless of the speeds of the two objects? ______ Comment on your answer. 3. List possible sources of error in this lab. 3 CMSE Phys Graph s of Moti on in One Di mensi on Purpose: to examine and compare the shapes of position-time and velocity-time graphs for objects moving in one dimension Procedure: Use the simulation at the web site http://jersey.uoregon.edu/vlab/block/Block.html to complete the summary table illustrating shapes of graphs for objects experiencing one-dimensional motion. Use the knowledge you gain from this simulation and class discussion to complete the parts of the table illustrating motion that the simulation will not run. Initial Position Initial Velocity Acceleration 0 Positive 0 0 Negative 0 0 0 Positive 0 0 Negative Positive 0 Positive Positive 0 Negative Sketch of Position-Time Graph Sketch of Velocity-Time Graph 1 CMSE Phys Initial Position Initial Velocity Acceleration Negative 0 Positive Negative 0 Negative 0 Positive Positive 0 Positive Negative 0 Negative Positive 0 Negative Negative Positive Positive 0 Positive Negative 0 Negative Positive 0 Negative Negative 0 Positive Positive Positive Sketch of Position-Time Graph Sketch of Velocity-Time Graph 2 CMSE Phys Initial Position Initial Velocity Acceleration Positive Positive Negative Positive Negative Positive Positive Negative Negative Negative Positive Positive Negative Positive Negative Negative Negative Positive Negative Negative Negative 0 0 0 Negative 0 0 Positive 0 0 Sketch of Position-Time Graph Sketch of Velocity-Time Graph 3 CMSE Phys Questions: 1. What is indicated by a velocity-time graph that crosses the x-axis? 2. How can you tell by looking at a position-time graph whether or not the object was changing speed? 3. How can you tell by looking at a velocity-time graph whether or not the object was changing speed? 4. What is the effect of changing the initial position on position-time and velocity-time graphs? 5. What is represented by the y-intercept on a position-time graph? 6. What is represented by the y-intercept on a velocity-time graph? 7. What is represented by an x-intercept on a position-time graph? 8. What is represented by an x-intercept on a velocity-time graph? 9. No matter what the initial position and initial velocity are, the velocity-time graph of an object with a positive acceleration will always … 10. No matter what the initial position and initial velocity are, the velocity-time graph of an object with a negative acceleration will always … 11. No matter what the initial position and initial velocity are, the velocity-time graph of an object with no acceleration will always … 4 CMSE Phys Accel era tion Do wn an Incli ne There is a well-known story that Galileo dropped two objects of different weights from the Leaning Tower of Pisa in order to show that all objects accelerate toward the Earth at the same rate, regardless of their weight as long as air resistance is negligible. Historians, however, are quite certain that Galileo never performed such an experiment. Galileo’s experiments with acceleration involved rolling balls down an inclined plane. He did this out of necessity because of hi s inability to make precise measurements of the small distances and short time intervals needed for measuring the acceleration of objects in free fall. The inclined plane’s angle could be adjusted until the time for the ball to roll to the end was long enough for even the crude time -measuring devices of his day to produce useful results. In this exercise, you will examine acceleration by measuring the time needed for an object to roll various distances down an inclined plane – much like Galileo did around 400 years ago. Purpose: 1. Examine the acceleration of a object rolling down an inclined plane 2. Determine the shape of a “Distance vs Time” graph for an accelerating object 3. Determine the mathematical relationship between the distance and time an object travels while it is accelerating Materials: inclined plane, marble, stopwatch, meter stick or measuring tape Procedure: 1. 2. 3. 4. 5. 6. 7. Measure and mark from one end of the inclined plane the distances indicated in the data table. Place your inclined plane on something (a book?) so that one end is slightly elevated. Use the stopwatch to determine how much time is needed for the marble to roll each indicated distance down the incline. Record this time in the data table. Perform three time trials for each distance and average them. Use MS Excel to make a graph of “Distance vs Time.” Use the MS Excel “Add Trendline” function to draw and calculate the best-fit curve to your data points. Place this on your graph. Answer the questions at the end of this activity. 1 CMSE Phys Distance, meters 0.10 0.15 0.20 0.40 0.50 0.60 0.70 0.80 0.90 1.20 1.35 1.60 1.80 Trial 1 Time, seconds Trial 2 Trial 3 Average Time, seconds Questions: 1. How does a “distance vs time” graph of accelerated motion compare with a “distance vs time” graph of non-accelerated motion (constant velocity)? 2. How can you tell by looking at a “distance vs time” graph whether or not the object has constant or changing speed? 3. What does the shape of your graph and the “best-fit” equation tell us about the mathematical relationship between distance and time for a uniformly accelerating object? 4. When looking at his data, Galileo discovered that an object would travel 4 times as far (22 ) in twice the time, 9 times as far (32 ) in triple the time, 16 times as far in (42 ) in quadruple the time, etc... Use your graph to find the …. 2 CMSE Phys time time time time time time to to to to to to travel travel travel travel travel travel 0.40 m ____ 0.60 m ____ 0.80 m ____ 1.00 m ____ 1.20 m ____ 1.60 m ____ time to travel 0.10 m ____ time to travel 0.15 m ____ time to travel 0.20 m ____ time to travel 0.25 m ____ time to travel 0.30 m ____ time to travel 0.40 m ____ ratio ratio ratio ratio ratio ratio = = = = = = ____ ____ ____ ____ ____ ____ time to travel 0.90 m ____ time to travel 1.35 m ____ time to travel 1.80 m ____ time to travel 0.10 m ____ time to travel 0.15 m ____ time to travel 0.20 m ____ ratio = ____ ratio = ____ ratio = ____ 5. Do your results seem to agree with Galileo’s discovery? _____ Why/Why not? 6. What could you do in order to experimentally test whether or not all objects accelerate at the same rate, regardless of their weight? 7. How do you think the angle of incline affects this experiment? 8. What should happen to the time values in your data table if the incline is made steeper? 9. What should happen to the ratios in question #4 if the incline is made steeper? 10. List possible sources of error in this lab. 3 CMSE Phys A ccel era tio n of a Fr eely F allin g Objec t: A Vi rt ual Ac tivity Purpose: 1. Examine distance-time and velocity-time graphs of a freely falling object. 2. Determine the acceleration due to gravity of an object in "free fall." Procedure: 1. Go to the web site http://jersey.uoregon.edu/vlab/AverageVelocity/index.html . 2. Complete Data Table I by running the simulation in order to determine through “trial and error” the distance the object falls during the specified times. 3. Use MS Excel to make a graph of "Total Distance Fallen vs. Time." 4. Use the “Add Trendline” function to determine and place the “best fit” equation on your graph. 5. Print your graph, making sure it is labeled properly. 6. How can you tell by looking at a position-time graph whether or not the object had a constant velocity (speed)? Data Table I Time, s Distance, m 0.0 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 1.00 1.05 1.10 1 CMSE Phys To find out how the velocity (speed) changed and obtain the acceleration as the object fell, you must first calculate average velocities (speeds) of specific time intervals. For convenience, you will calculate the average velocity (speed) during every tenth of a second. You will then see how these speeds changed with time. 5. Subtract distances from Data Table I to find the distances the object fell during every tenth of a second. Record these distances in Data Table II as Interval Distances. 6. Calculate the average velocity (speed) during each of these intervals using the relationship average speed = distance/time. The time for each interval will be 0.10 s. Record these values in the data table. 7. Using the assumption that a freely falling object increases its speed uniformly, we can conclude that the average speed during the interval will equal the instantaneous speed at the time halfway through the interval. Therefore, the instantaneous velocity (speed) at time t = 0.15 s will be the same as the average velocity (speed) during the time from t = 0.10 s to t = 0.20 s. Data Table II Time Interval, s Time of Interval, s 0.00 - 0.10 0.10 - 0.20 0.20 - 0.30 0.30 - 0.40 0.40 - 0.50 0.50 - 0.60 0.60 - 0.70 0.70 - 0.80 0.80 - 0.90 0.90 - 1.00 1.00 - 1.10 0.10 0.10 0.10 0.10 0.10 0.10 0.10 0.10 0.10 0.10 0.10 Interval Distance, m Average Velocity for Interval, m/s Avg. Vel. = Inst. Vel. at Time…, s 0.05 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 0.95 1.05 2 CMSE Phys 8. Use MS Excel and the last two columns in Data Table II to make a graph of “Instantaneous Velocity vs Time.” 9. Use the “Add Trendline” function to determine and place the “best fit” equation on your graph. 10. Print this graph, making sure it is labeled properly. Discussion Questions: 1. The slope of your “Instantaneous Velocity vs Time” graph should be the value of the object’s acceleration. The slope of our graph is __________. 2. Make a statement comparing your acceleration to the accepted value of 9.8 m/s/s. 3. Look at the equation for your “Total Distance Fallen vs Time” graph. How can you determine the value of the gravitational acceleration from that equation? 4. Even though this activity was performed using a computer simulation, your results may not be in exact agreement with the accepted value for gravitational acceleration. What are some reasons why an activity such as this might still have error in it? Extension Idea: Repeat this process simulating free fall on Mars or the Moon. (not required, but something else that could be done) 3 CMSE Phys Resul tan t V ect ors Part I. Calculate the resultant vectors when the following sets of vectors are combined. Show all steps as directed in class and illustrated by this example. A = 40 N @ 30° SE B = 60 N @ 70° SW Ax = 40 cos 30° = 34.64 Bx = - 60 cos 70° = - 20.52 Rx = Ay = - 40 sin 30° = - 20.00 By = - 60 sin 70° = - 56.38 14.12 Ry = - 76.38 R2 = Rx 2 + Ry2 = (14.12)2 + (- 76.38)2 = 6033.28, so R = 77.67 N T = Tan-1 (Ry/Rx) = Tan-1 (76.38/14.12) = 79.53° SE Solution: R = 77.67 N @ 79.53° SE Part II. Using either the “head-to-tail” or “head-to-head” graphical method, construct the resultant vectors when these same sets of vectors are combined. Use a scale of 1.0 cm = 1.0 unit. Measure the magnitude and direction of the resultant and compare with your calculated resultant. Label all vectors as directed in class. 1. A = 35 N @ 60° NE, B = 50 N @ 20° NW 2. A = 70 m/s @ 60° SW, B = 50 m/s @ 70° NW 3. A = 40 m @ 60° SE, B = 80 m @ 30° NW 4. A = 15 lb @ 60° NE, B = 50 lb @ 20° SE 5. A = 35 N @ 40° SW, B = 65 N @ 20° NW, C = 65 N @ 20° NE 6. A = 75 N @ 10° NE, B = 50 N @ 20° NW, C = 65 N @ 70° SE Softball Throw The initial velocity of a projectile may be found by measuring the amount of time it is in the air, the horizontal distance it travels during that time, and applying these values to a few simple calculations. Procedure: Record the name of the person throwing the softball. Throw the ball and measure the distance, in feet, and the time, in seconds, the ball travels through the air and record these values in the appropriate place in the data table. Repeat this procedure until this portion of the data table is complete. Use the formula d x = vxt to find the horizontal velocity, in ft/s, for each trial. Record these values in the data table. To find the initial vertical velocity, vy, use the formula vy = gt, where g is the acceleration of gravity and t is the time for the upward trip of the ball only. Use g = 32 ft/s/s and one-half of the total time in the air. Record these values in the data table. You now have the horizontal and vertical components of the initial velocity. Use the Pythagorean Theorem (v2 = vx2 + vy2 ) to calculate the magnitude of the initial velocity in ft/s. Record these values in the data table. To convert these speeds from ft/s to mph, use the relationship that 1 mile = 5280 feet and 1 hour = 3600 sec. Record these values in the data table. Divide the vertical velocity by the horizontal velocity and find the inverse tangent of this result to find the angle above the horizontal that the ball was thrown. Record these values in the data table. The maximum height, in feet, the ball traveled above the release point is found by squaring the vertical velocity (in ft/s) and dividing by twice the acceleration of gravity (2 x 32 ft/s/s = 64 ft/s/s). 1 Data Table Name Horizontal Distance, feet Time, seconds Horizontal Velocity, ft/s Vertical Velocity, ft/s Velocity, ft/s Velocity, mph Angle, θ Maximum height, ft 2 CMSE Phys Newton’s 2nd Law: Acceleration of a Pulley System A “Virtual” E xercise According to Newton’s 2nd Law, the acceleration of an object is inversely proportional to its total mass and directly proportional to the net force acting on it. Go to the web site http://physics.bu.edu/~duffy/java/Rotation2.html . You will see a drawing identical to the one to the right. Run the simulation while adjusting the masses of the red and blue blocks in order to examine Newton’s Second Law. For the first trials, you will keep a constant total mass of 10 kg. By “moving” mass from one side to the other, you will vary the net force. 1. Run the simulation using the masses shown in Data Table I, using a mass of zero for the pulley. 2. Record the acceleration shown in the simulation. 3. Calculate the weights of the blocks. (Use g = 9.8 m/s/s when calculating the weights.) 4. The net force will be the difference in the weights (Blue weight – Red weight). 5. Make a graph of Acceleration vs Net Force when Total Mass is Constant. 6. Does the shape of your graph confirm the relationship between acceleration and net force that Newton’s Law predicts? 1 CMSE Phys Data Table I - Experimental Results: Constant Mass Block Mass, kg Red Blue 1 9 2 8 3 7 4 6 5 5 6 4 7 3 8 2 9 1 Total Mass, kg Block Weight, N Red Blue Net Force, N Acceleration, m/s/s For these next trials, you will keep a constant net force of 9.8 N. By “adding” mass to each side of the pulley, you can maintain the same net force while varying the total mass. 1. Run the simulation using the masses shown in Data Table II, using a mass of zero for the pulley. 2. Record the acceleration shown in the simulation. 3. Calculate the weights of the blocks. (Use g = 9.8 m/s/s when calculating the weights.) 4. The net force will be the difference in the weights (Blue weight – Red weight). 5. Use MS Excel to make a graph of Acceleration vs Total Mass when the Net Force is Constant. 6. Does the shape of your graph confirm the relationship between acceleration and total mass that Newton’s Law predicts? 2 CMSE Phys Data Table II - Experimental Results: Constant Net Force Block Mass, kg Red Blue 1 0 2 1 3 2 4 3 5 4 6 5 7 6 8 7 9 8 Total Mass, kg Block Weight, N Red Blue Net Force, N Acceleration, m/s/s 3 CMSE Phys Newton’s 2nd Law: Mass on Table System A “Virtual” E xercise • • • • Go to the site http://webphysics.ph.msstate.edu/jc/library/4-7a/index.html . Click on “Start Simulation.” You will open a window identical to the one shown below. Run the simulation while adjusting the mass of the wagon and the hanging mass in order to examine Newton’s Second Law. • According to Newton’s 2nd Law, the acceleration of an object is inversely proportional to its total mass and directly proportional to the net force acting on it. Part I: For the first trials, you will keep a constant total mass of 200 g. By “moving” mass from the wagon to the hanger, you will vary the net force. 1. Run the simulation using the masses shown in the data table and setting the friction coefficient to zero. 2. Record the acceleration shown in the simulation. How would you calculate these values if they were not given to you in the simulation? 3. Calculate the weight of the hanging mass. (Use g = 9.8 m/s/s when calculating this weight.) 1 CMSE Phys 4. Since there is “no friction,” the net force is equal to the weight of the hanging mass. 5. Make a graph of Acceleration vs Net Force when Total Mass is Constant. 6. Does the shape of your graph confirm the relationship between acceleration and net force that Newton’s 2nd Law predicts? Experimental Results: Constant Mass Mass, kg Wagon Hanging 0.199 0.175 0.150 0.125 0.100 0.075 0.050 0.025 0.001 0.001 0.025 0.050 0.075 0.100 0.125 0.150 0.175 0.199 Total Mass, kg Net Force, N (Weight of the Hanging Mass) Acceleration, m/s/s 0.200 0.200 0.200 0.200 0.200 0.200 0.200 0.200 0.200 Part II: For these next trials, you will keep a constant net force of 0.49 N (by keeping a constant mass of 50 g on the hanger). By “adding” mass only to the wagon, you can maintain this same net force while varying the total mass. 1. Run the simulation using the masses shown in the data table, again setting the friction coefficient to zero. 2. Record the acceleration shown in the simulation. How would you calculate these values if they were not given to you in the simulation? 3. Calculate the weight of the hanging mass. (Use g = 9.8 m/s/s when calculating this weight.) 4. Since there is “no friction,” the net force is the weight of the hanging mass. 5. Make a graph of Acceleration vs Total Mass when the Net Force is Constant. 6. Does the shape of your graph confirm the relationship between acceleration and net force that Newton’s 2nd Law predicts? 2 CMSE Phys Experimental Results: Constant Net Force Mass, kg Wagon Hanging 0.010 0.030 0.070 0.100 0.150 0.250 0.350 0.500 0.650 0.800 0.900 0.050 0.050 0.050 0.050 0.050 0.050 0.050 0.050 0.050 0.050 0.050 Total Mass, kg Net Force, N (Weight of the Hanging Mass) Acceleration, m/s/s Questions: 1. How would you calculate the acceleration of the system if friction were present? 2. Suppose there is no friction. In order for the wagon on the table to move, the weight hanging over the side of the table must be at least… 3. Suppose friction is present. In order for the wagon on the table to move, the weight hanging over the side of the table must be at least…. 4. Is it possible to obtain an acceleration equal to the gravitational acceleration if friction is not present? Why or why not? 3 CMSE Phys The Simple Pendulum Objectives: 1) To determine if/how mass, length, and angular displacement affect the period of a simple pendulum 2) Use a simple pendulum to determine the acceleration of gravity Materials: light string, meter stick, stopwatch, various masses • • • • Your simple pendulum will consist of a mass suspended by light thread from a point about which it can freely swing. The displacement of the pendulum will be the angle at which it is pulled back before release to swing. The length is the distance from the point of suspension to the center of gravity of the mass. You will measure the period (the time it takes for the pendulum bob to swing from one side to the other and back again) while individually varying the mass, length, and angular displacement of the pendulum. I. DOES MASS AFFECT THE PERIOD OF A PENDULUM? A. Use a length of string between 0.60 m and 1.20 m. Tie a mass to the string. Pull the pendulum bob back about 30° and record the time it takes for the pendulum to make 10 complete cycles. Divide this time by 10 to get the period of the pendulum. B. Record this information in DATA TABLE I. C. Now perform the same procedure, but use a different mass. Be sure to keep all other variables EXACTLY the same as before. D. Repeat these steps for the other masses. Record all information in the data table. II. DOES LENGTH AFFECT THE PERIOD OF A PENDULUM? A. Find the period of the pendulum as you did above, but use the same mass and amplitude in each trial, while varying only the pendulum’s length. B. Do this according to DATA TABLE II. III. DOES AMPLITUDE AFFECT THE PERIOD OF A PENDULUM? A. This time use a constant length and mass, but vary the amplitude (angle) through which the pendulum swings. B. Find the period of the pendulum with initial amplitudes given in DATA TABLE III. C. Record all information in the data table. Find the formula for the pendulum in your book and use your results to calculate the acceleration of gravity for each trial. 1 CMSE Phys DATA TABLE I – Variable Mass Mass, g Length, m Amplitude, deg Time, s 10 cycles Period, s g, m/s2 Time, s 10 cycles Period, s g, m/s2 Time, s 10 cycles Period, s g, m/s2 20 50 100 200 500 DATA TABLE II – Variable Length Mass, g Length, m Amplitude, deg 0.20 m 0.35 m 0.50 m 0.65 m 0.80 m 0.95 m 1.10 m 1.25 m 1.40 m DATA TABLE III – Variable Amplitude Mass, g Length, m Amplitude, deg 10 20 30 40 50 2 CMSE Phys Results : Make a graph of “Period vs Mass” using the results of Data Table I. Make a graph of “Period vs Length” using the results from Data Table II. Make a graph of “Period vs Amplitude” using the results of Data Table III. On each graph, write a statement commenting on the relationship between the period and the manipulated variable that is indicated by the shapes of the graphs. For example, you may find relationships that are directly proportional, inversely proportional, quadratic, square root, sinusoidal, or you may find no relationship at all. Write a summary paragraph describing what you learned about pendulums from this activity. 3 CMSE Phys Sliding Friction Objectives: • determine the coefficient of sliding friction for wood on desk , rubber-soled shoe on dry floor, and rubber-soled shoe on wet floor • determine the relationship between friction force and surface area Equipment: force scale, friction block, shoe, various masses, water Procedure: “Wood on Desk - Wide Side” 1. Find the weight of your friction block using either the triple beam balance or your force scale. 2. Record the weight of the friction block in Data Table I. 3. Attach the force scale to the friction block and pull the scale horizontally with the desktop at a steady rate and record the average force reading in your data table under the column “Friction Force.” 4. Add some mass. Calculate this additional weight (use g = 10 m/s/s for each of the calculations) and record your findings in the Data Table. This total amount of weight will be known as the “Normal Force.” Pull the block as before to find the amount of friction force with this total weight. 5. Continue until Data Table I is completed with 5 total trials. 6. Calculate the “Friction Coefficient” by dividing the Friction Force by the Normal Force. This coefficient has no units since you are dividing Newtons by Newtons. 7. Find the average value of your friction coefficients and record beneath your data table. 8. Make a graph of “Friction Force vs. Normal Force.” Include the origin as one of your data points. Determine the best fit equation of your line and record on the graph. Notice how close the slope is to your average Friction Coefficient. 1 CMSE Phys “Rubber-soled Shoe on Dry Floor” 9. Repeat procedures 1-8 using the shoe on the dry floor for Data Table II – “Rubber-soled Shoe on Dry Floor.” Data Table I – “Wood on Desk - Wide Side” Trial Block Weight, N 1 2 3 4 5 Additional Mass, kg 0 Additional Weight, N 0 Normal Force (Total Weight) N Friction Force, N Friction Coefficient Average Friction Coefficient for “Wood on Desk” = __________ Data Table II – “Rubber-soled Shoe on Dry Floor” Trial 1 2 3 4 5 Shoe Weight, N Additional Mass, kg 0 Additional Weight, N 0 Normal Force (Total Weight) N Friction Force, N Friction Coefficient Average Friction Coefficient for “Rubber-soled Shoe on Dry Floor” = __________ 2 CMSE Phys 10. Repeat procedures 1-8 using the shoe on a place where you have made the floor wet. Record the results in Data Table III – “Rubber-soled Shoe on Wet Floor.” Data Table III – “Rubber-soled Shoe on Wet Floor” Trial 1 2 3 4 5 Shoe Weight, N Additional Mass, kg 0 Additional Weight, N 0 Normal Force (Total Weight) N Friction Force, N Friction Coefficient Average Friction Coefficient for “Rubber-soled Shoe on Wet Floor” = __________ Compare the friction coefficient of rubber on a dry floor with rubber on a wet floor. You will now repeat these procedures for finding the friction coefficient for wood on desk, but will use the “thin side” of the wood block. Since the “wide side” has approximately ______ times as much area as the “thin side,” most people would expect the friction on the “wide side” to be about _____ times as large. 3 CMSE Phys 11. Perform these trials as before and record your results in Data Table IV - “Wood on Desk - Thin Side.” Data Table IV – “Wood on Desk – Thin Side” Trial Block Weight, N 1 2 3 4 5 Additional Mass, kg 0 Additional Weight, N 0 Normal Force (Total Weight) N Friction Force, N Friction Coefficient Average Friction Coefficient for “Wood on Desk – Thin Side” = __________ Questions: 1. How does the friction coefficient depend on the area of the surface in contact? 2. Why do you think this is so? 3. What factors do influence the amount of sliding friction? 4. Name some possible sources of error in this lab. 4 CMSE Phys Data Table V – “ Trial Block Weight, N 1 2 3 4 5 Additional Mass, kg 0 Additional Weight, N 0 1 2 3 4 5 Block Weight, N Additional Mass, kg 0 ” Normal Force (Total Weight) N Average Friction Coefficient for “ Data Table VI – “ Trial on Friction Force, N on on Additional Weight, N 0 ” = __________ ” Normal Force (Total Weight) N Average Friction Coefficient for “ Friction Coefficient Friction Force, N on Friction Coefficient ” = __________ 5 CMSE Phys Forces in Equilibrium According to Newton’s First Law of Motion, an object remaining at rest even when forces are acting upon it does so because there is no net force acting on the object. This means that the resultant or vector sum of all the forces acting on the object is zero. An object in this state or condition is said to be “in equilibrium.” In this lab exercise, you will apply forces to an object in such a way that the object remains stationary. You will then verify that the resultant force is indeed zero. 1. Place the ring (washer) over the origin of your polar grid paper with the force scales attached in the positions indicated in the data table. 2. Pull each scale in the indicated directions. Pull so that the ring remains centered over the origin. At least one of your forces should be over 15.0 N. 3. Record the reading on each scale. Record to the nearest tenth of a Newton when using these 0-20 N scales. 4. Calculate the horizontal (x) and vertical (y) components of each force. 5. Sum the components. Record these values in the data tables. 6. Use the Pythagorean Theorem and the inverse tangent function to calculate each resultant force’s magnitude and direction. Your resultant magnitudes should be close to zero. A B C Force (Newtons) Angle (Degrees) 0 (East) 110 (70° NW) 200 (20° SW) Sum of Components = Horizontal Component Vertical Component Force (Newtons) Horizontal Component Vertical Component Resultant = A B C Angle (Degrees) 45 135 (45° NW) 270 (South) Sum of Components = Resultant = 1 CMSE Phys Force (Newtons) A B C Angle (Degrees) 80 210 (30° SW) 280 (80° SE) Sum of Components = Horizontal Component Vertical Component Angle (Degrees) 60 190 (10° SW) 340 (20° SE) Horizontal Component Vertical Component Angle (Degrees) 25 180 (West) 335 (25° SE) Horizontal Component Vertical Component Resultant = Force (Newtons) A B C Sum of Components = Resultant = Force (Newtons) A B C Sum of Components = Resultant = A B C D E Join with another group for this final trial. Force Angle Horizontal (Newtons) (Degrees) Component 0 (East) 20 120 (60° NW) 240 (60° SW) 315 (45° SE) Sum of Components = Vertical Component Resultant = 2 CMSE Phys Graph constructed using a free graphing program found at http://www.mathematicshelpcentral.com/graph_paper.htm 3 CMSE Phys Torque and Rotational Equilibrium In this lab, you will pull on a meter stick at various locations until the meter stick is “at rest” (neither translating nor rotating, which is a state of equilibrium). You will then verify the two conditions for equilibrium by examining the total amounts of upward and downward force and the total amounts of clockwise and counterclockwise torques. 1. Place the scales at the locations indicated. Scales A and C should pull in the same direction, with scale B (and D if given) pulling in the opposite direction. Place arrows on the meter stick diagram in order to show the location of each force. 2. Record the readings on each scale when equilibrium is achieved. 3. Use the “zero” end of the meter stick as your pivot point and calculate your torques (in this lab, “torque = force x location” since the location is the distance from the zero end). 4. Sum the forces and torques. Look at each of these values to see how well each trial verified the conditions for equilibrium. I. Scale A B C Location, cm 20 50 80 Force, N Up or Down? Torque, N•cm 0 cm cw or ccw? 100 cm Σ Fup Σ Fdown Σ τcw Σ τccw II. Scale A B C Location, cm 30 60 90 Force, N Up or Down? Torque, N•cm 0 cm cw or ccw? 100 cm Σ Fup Σ Fdown Σ τcw Σ τccw 1 CMSE Phys III. Scale A B C Location, cm 10 70 90 Force, N Up or Down? Torque, N•cm 0 cm cw or ccw? 100 cm Σ Fup Σ Fdown Σ τcw Σ τccw IV. Scale A B C D Location, cm 25 40 70 80 Force, N Up or Down? Torque, N•cm 0 cm cw or ccw? 100 cm Σ Fup Σ Fdown Σ τcw Σ τccw V. Scale A B C D Location, cm 5 50 70 85 Force, N Up or Down? Torque, N•cm 0 cm cw or ccw? 100 cm Σ Fup Σ Fdown Σ τcw Σ τccw 2 CMSE Phys POWER A simple way to measure the power output of a person is to measure the time it takes the person to walk/run up a flight of stairs (or bleachers). In this experiment you will measure your power in climbing a flight of stairs and compare it to the power of your classmates. 1. Measure the height from the ground to the second floor/top of stairs (or other desired position). 2. Record your name and weight (in pounds) or use the scale to obtain your mass (in kilograms). 3. Measure the time it takes to run (or walk) to the desired height. 4. Share your values with your classmates and record their values in the data table. After everyone has run (or walked) up the stairs, perform the following calculations to find the power. 1. Convert a weight from pounds to Newtons by dividing the weight in pounds by 2.2 to get the mass in kilograms. Then multiply the mass (in kilograms) by 9.8 m/s/s to obtain the weight in Newtons. 2. Find the amount of work (in Joules) each person has done by multiplying their weight (in Newtons) by the height ascended (in meters). 3. Find the power (in Watts) using the formula: Power (W) = Work (J) / time (sec). 4. Find the equivalent horsepower by dividing the power (in Watts) by 746 because 1 horsepower equals 746 Watts. 5. Record all values in the data table. 1 CMSE Phys **** Alternative Procedure **** Find the power output in doing work on an object (a brick, book bag, etc...). Weigh the object and carry it up the stairs or pull it up using a rope. Calculate the power exactly as described above. In the data table, write “your name carrying or lifting item” under the “Name” column. Questions: 1. The work done in traveling up the flight of stairs (or lifting an object) depends only on … 2. Power depends on … 3. How would the work done in lifting a load up three flights of stairs compare to the work done in lifting the same load up one flight of stairs? 4. What happens to the power output if the same amount of work is done in one-half the time? 5. What happens to the power output if the same amount of work is done in twice the time? 6. How much work (energy) is needed to keep a 100 W light bulb lit each second? 7. How much work (energy) is needed to keep a 100 W light bulb lit each minute? 8. How much work (energy) is needed to keep a 100 W light bulb lit each hour? 9. The same amount of work (energy) needed to keep the 100 W light bulb lit for one hour could be used to lift a 2000 kg SUV to what height? 2 CMSE Phys POWER DATA TABLE Name Weight (lbs) Mass (kg) Weight (N) Height (meters) Work (Joules) Time (sec) Power (Watts) Power (hp) 3 CMSE Phys Wave Modeling Purpose: • • model transverse and longitudinal waves identify and measure wave characteristics Materials: • “butcher” paper ( 5-7 feet long, 2-3 feet wide), stopwatch, meter stick, markers Procedure: Each group should have three members. Place the large sheet of butcher paper on the lab table. One group member steadily pulls the paper across the table while another member moves the marker back and forth over the paper. The arm should swing freely as a pendulum. The third group member uses the stopwatch to measure the amount of time needed to sketch the wave motion across the entire length of paper. A transverse wave may be modeled when the marker moves back and forth perpendicularly to the direction of the moving paper. A longitudinal wave may be modeled when the marker moves back and forth across the paper parallel to its direction of movement. If done carefully, you should see nice consistent shapes for these two wave models. For each of these two wave models: • • • • • • • Record the total time of the wave motion on the paper. Label, measure, and record the wavelength of the wave. Label, measure, and record the amplitude of the wave. Count the number of complete vibrations and divide by the total time to obtain the frequency of the wave. Divide the total time by the number of complete vibrations to obtain the period of the wave. Find the wave’s velocity by measuring the total distance the wave traveled and dividing this value by the total time. Now calculate the wave’s velocity by multiplying the recorded frequency of the wave by the measured wavelength. Compare this result with the velocity obtained using the total distance and time. Show all work and calculations on the butcher paper. CMSE Phys PULSES ON A COIL SPRING Coiled springs are excellent materials for analyzing a variety of wave behaviors. In this activity, you will examine transverse and longitudinal pulses, fixed- and free-end reflections, constructive and destructive interference, standing waves, and the behavior of waves when they reach new transmitting media. TRANSVERSE PULSES A. Send a transverse pulse down a stretched large coil spring. Observe the motion of the spring’s coils. Draw a sketch of the pulse traveling down the spring. Why is this pulse called a transverse pulse? B. Observe the speed of the pulse while varying the pulse amplitude. What happens to the speed of the pulse as the amplitude changes? C. Observe the speed of the pulse while varying the tension in the spring. What do you notice about the pulse speed with respect to changes in tension? D. Does the stretched spring under different tensions represent the same or different transmitting media? E. Maintain a constant tension and send continuous wave trains of varying frequencies down the spring. What happens to the wavelength as the frequency increases? 1 CMSE Phys WAVE INTERFERNCE F. Send two pulses of approximately the same amplitude from opposite ends of the spring toward each other on the same side of the spring. What do you observe? Do the two disturbances “bounce off” each other or pass right through each other? What do you notice when the pulses “overlap”? Draw sketches showing the pulses, labeled “A” and “B”, before, during, and after they meet. G. Send two pulses of approximately the same amplitude from opposite ends of the spring toward each other on opposite sides of the spring. What do you observe? Do the two disturbances “bounce off” each other or pass right through each other? What do you notice when the pulses “overlap”? Draw sketches showing the pulses (labeled “A” and “B”) before, during, and after they meet. 2 CMSE Phys WAVE REFLECTION H. Hold the spring firmly down in place at the far end and send a pulse down the spring. Describe and illustrate your observations of reflection from this “fixed end.” I. Attach and hold a light string on one end of the spring and send a pulse from the other end. Describe and illustrate your observations of reflection from this “free end.” WAVE BEHAVIOR AT MEDIA BOUNDARIES J. Attach the two springs together and send a pulse from the large spring. Record your observations. K. What happens to the wave speed when the pulse goes from the large spring to the small spring? .…from the small spring into the large spring? L. Did you notice any reflection when the pulse reached the junction where the two springs were connected? Did more of the wave seem to be transmitted or reflected? Think of a common example where light waves partially reflect and partially transmit when they reach the boundary of the transmitting media. 3 CMSE Phys STANDING WAVES M. While holding one end of the large spring firmly in place, move the other end of the spring continuously back and forth to send a continuous wave train down the spring. Adjust your frequency until a standing wave with two “loops” is obtained. Now change your frequency of vibration until more loops are formed. Since the speed of the wave remains constant (do you know why?), shaking the spring with a higher frequency does what to the wavelength? In order to obtain standing waves with more loops when the speed of the wave is constant, what must be done to the frequency of vibration? How could you determine the wavelength of the wave when a standing wave pattern is observed? Draw sketches of standing waves having one, two, three, and four loops. Indicate on your sketches how the wavelength could be measured. LONGITUDINAL PULSES N. Stretch the large spring and send a longitudinal pulse down the spring. Observe the motion of the spring coils. Draw a sketch of the pulse traveling down the spring. Why is this pulse called a longitudinal pulse? Note: Wave properties such as diffraction and refraction unfortunately cannot be observed with coiled springs. 4 CMSE Phys Waves in a Ripple Tank: A Virtual Activity Go to the site http://www.falstad.com/oscgrid/ . A “Ripple Tank Applet” window will open that runs a simulation of waves generated in a ripple tank. By “clicking on” any or all of the three task bars in the upper right hand corner of the applet window, you can change the type and number of wave sources. The third task bar allows you to use the mouse to edit the waves or walls (barriers). You can adjust the speed, resolution, frequency, brightness, and/or damping of the wave simulation to obtain a clearer representation of the wave phenomena. A complete and detailed set of directions for how to use this simulation is linked to the web page. Your task is to use this web site to identify and investigate various wave properties and characteristics. You will hand in pictorial representations of… 1. Circular Wave a. long wavelength b. shorter wavelength 2. Plane Wave a. long wavelength b. shorter wavelength 3. Reflection a. Plane Wave Off Angled Straight Barrier b. Plane Wave Off Concave (Parabolic) Barrier c. Circular Wave Off Straight Barrier 1 CMSE Phys 4. Diffraction a. Plane Wave Around a Barrier b. Plane Wave Through an Opening c. Circular Wave Around a Barrier d. Circular Wave Through an Opening 5. Refraction of a Plane Wave 6. Refraction due to Temperature Gradient (simulates sound wave over lake) 7. Interference a. Two Circular Waves (wide spacing between sources) b. Two Circular Waves (closer spacing between sources) c. One Plane and One Circular Wave (this is a tricky one to simulate!) d. Single Slit (plane wave) e. Double Slit (plane wave) f. Triple Slit (plane wave) 8. Doppler Effect 9. Beats 10. Something else you find really interesting You have two options for completing this assignment: 1. Make small (about 4 in. x 4 in.) sketches with colored pens/pencils…OR… 2. Use a “screen capture” program to copy and paste the actual images from the applet window into a document (MS Word with text boxes, for example), which can then be saved and printed. You can download a free trial version of an easy to use screen capture program at http://www.etrusoft.com/ . The image shown on this handout was “captured” using this program. You can probably fit 6 diagrams/sketches on each side of a page. Be sure to label each sketch. 2 CMSE Phys Resonance: The Speed of Sound – Closed Tube Trial Tuning Fork Frequency, Hz Resonant Tube Length, m Tube Diameter, m Wavelength, m Experimental Speed of Sound, m/s Air Temp, °C Accepted Speed of Sound, m/s Percent Error, % 1 2 3 4 FOR EACH TRIAL 1. Calculate the wavelength of each resonant sound wave. Show the formula and calculations in the space below. 2. Calculate the experimental speed of sound. Show the formula and calculations in the space below. 3. Use the air temperature to find the accepted speed of sound. Show the formula and calculations in the space below. 4. Calculate the % error for each speed of sound trial. Show the formula and calculations in the space below. 1 CMSE Phys You will now use the phenomenon of resonance to determine the frequency of an unmarked tuning fork. Trial Resonant Tube Length, m Tube Diameter, m Wavelength, m Air Temp, °C Accepted Speed of Sound, m/s Calculated Tuning Fork Frequency, Hz 1 2 FOR EACH TRIAL 1. Find the resonant tube length and calculate the wavelength of each resonant sound wave. Show the formula and calculations in the space below. 2. Use the air temperature to find the accepted speed of sound. Show the formula and calculations in the space below. 3. Use the experimental wavelength and temperature-based accepted speed of sound to calculate the frequency of your tuning fork. Show the formula and calculations in the space below . 4. List sources of error in this lab. 2 CMSE Phys PALM PIPES Materials: ½ inch PVC pipe cut to the lengths listed below. The pipes can be marked with permanent marker or fingernail polish. The students hold the pipe in one hand and strike one of the open ends on the palm of the other hand, producing the pitch which corresponds to the length of the pipe. Note A Bb (A#) B C C# (Db) D D# (Eb) E F F# (Gb ) G Ab (G#) A Bb (A#) B C C# (Db) D D# (Eb) E F F# (Gb ) G Ab (G#) Length *(cm) 38.5 36.4 34.3 32.3 30.5 28.8 27.1 25.6 24.1 22.7 21.4 20.2 19.0 17.9 16.9 15.9 15.0 14.1 13.3 12.5 11.8 11.1 10.5 9.8 Frequency **(Hz) 220 233 247 261.5 277 293.5 311 329.5 349 370 392 415.5 440 466 494 523 554 587 622 659 698 740 784 831 * Lengths of these pipes are based on an air temperature of 20° C and 0.5 in diameter. ** Frequencies taken from http://ptolemy.eecs.berkeley.edu/eecs20/week8/scale.html Adapted and expanded from an activity presented by Hugh Henderson of Plano (Texas) Senior High School at the 2003 AP Physics Institute, Texas A&M University. 1 CMSE Phys MUSICAL SCALES Tonic C W D Third E Fourth F Fifth G Sixth A H B Tonic C C# D D# D# E F F F# G F# G G# G# A A# A# B C C C# D C# D D# E F F# F# G G# G# A A# A A# B B C C# C# D D# D# E F E F F# G G# A A A# B B C C# C C# D D D# E E F F# F# G G# G G# A A# B C C C# D D D# E D# E F F F# G G G# A A A# B A# B C Musical scales and chart taken from http://www.geocities.com/jayatea.geo/piano.html TWINKLE, TWINKLE LITTLE STAR (Nearly the same tune as the “Alphabet Song”) Twin - kle, twin - kle lit - tle star, How I won - der what you are Melody: F F C C D D C Bb Bb A A G G F Harmony: C C A A Bb Bb A G G F F E E C Melody: Harmony: Up a - bove the world so high, Like a dia - mond in the sky, C C Bb Bb A A G C C Bb Bb A A G A A G G F F C A A G G F F C Melody: Harmony: Twin - kle, twin - kle lit - tle star, How I won - der what you are F F C C D D C Bb Bb A A G G F C C A A Bb Bb A G G F F E E C 2 CMSE Phys HAPPY BIRTHDAY Hap - py birth - day to you, hap - py birth - day to you; C C D C F E C C D C G F Hap - py birth - day dear Ein - stein; C C C A F E D Hap - py birth - day to you! Bb Bb A F G F LONDON BRIDGE Lon - don bridge is fall - ing down, fall - ing down, fall - ing down; G A G F E F G D E F E F G Lon - don bridge is fall - ing down, my fair la - dy. G A G F E F B D G E C ROW, ROW, ROW YOUR BOAT Row, row, row your boat gen - tly down the stream; C C C D E E D E F G Mer - ri - ly, mer - ri - ly, mer - ri - ly, mer - ri - ly, C C C G G G E E E C C C Life is but a dream. G F E D C WHERE IS PINKY (POINTER, ETC…) (or Are You Sleeping?) “Where is Pin - ky? Where is Pin - key?” “Here I am! Here I am!” C D E C C D E C E F G E F G “How are you to - day sir?” “Ver - y well I thank you.” G A G F E C G A G F E C Run a - way, run a - way. C G C C G C 3 CMSE Phys SINGING CHIMES (adapted from Taylor, Poth, & Portman (1995), Teaching Physics with TOYS, Terrific Science Press: Middleton, Ohio. pp. 275-281) Chimes cut from 4 five-foot pieces of ½ inch aluminum pipe. Total cost of less than $8.00 (purchased as 2 ten-foot sections, Lowe’s Home Building Store, December 2003). Table 1: Chime Lengths Cut from pipe 2 Cut from pipe 3 Cut from pipe 1 Cut from pipe 4 Chime # Length (cm) Chime # Length (cm) Chime # Length (cm) Chime # Length (cm) 1 2 3 4 38.5 37.5 36.2 35.1 5 6 7 17 18 34.2 33.1 32.2 23.8 23.1 8 9 10 11 12 31.1 30.3 29.7 28.9 28.1 13 14 15 16 19 20 27.2 26.3 25.5 24.7 22.5 21.8 p. 276 Table 2: Chime Frequencies Chime # 1 2 3 4 5 6 7 p. 279 Note Frequency (Hz) Chime # Note Frequency (Hz) Chime # Note Frequency (Hz) F F# G G# A A# B 175 185 196 208 220 233 247 8 9 10 11 12 13 14 C C# D D# E F F# 262 277 294 311 330 349 370 15 16 17 18 19 20 G G# A A# B C 392 415 440 466 494 523 4 CMSE Phys SINGING CHIMES SONG SH EET (musical scores taken from Teaching Physics with TOYS, pp 280-281) MICHAEL ROW THE BOAT ASHORE Mi - chael row the boat a - shore 10 14 17 14 17 19 17 10 14 10 14 15 14 Mi - chael row the boat a - shore D F# A F# A B A D F# D F# G F# Hal - le - lu - a 14 17 19 17 10 14 15 14 Hal - le - lu - a F# A B A D F# G F# Mi - chael row the boat a - shore 14 17 17 14 15 14 12 10 14 14 10 12 10 9 Mi - chael row the boat a - shore F# A A F# G F# E D F# F# D E D C# Hal - le - lu - u - u - a 10 12 14 5 12 10 7 9 10 9 Hal - le - lu - u - u - a D E F# A E D B C# D C# HAPPY BIRTHDAY Hap - py birth - day 8 8 10 8 6 C C D C A# to 13 8 F C Hap - py birth - day 8 8 20 17 17 13 13 8 C C C A A F F C dear Ag - gie; 13 12 10 8 8 6 F C you, hap - py birth - day to 12 8 8 10 8 15 6 6 8 E C C D C G A# A# C E C you; 13 8 F C D A# Hap - py birth - day to you! 18 18 17 13 15 13 13 13 13 8 12 8 10 10 8 8 A# A# A F G F F F F C E C D D C C 5 CMSE Phys Plane Mirror Images Pre-Lab: Each group must complete and hand in their Pre-Lab Predictions before obtaining materials for this investigation. Learning Tasks: 1. Use the available resources (large plane mirror, text, computer simulation, peer counsel) to determine a plane mirror’s a) minimum length and b) vertical placement on a wall necessary for one to see a full length image when standing in front of the plane mirror. 2. Determine if/how this necessary mirror size and placement depends on an individual person’s height and distance away from the mirror. 3. Include a complete explanation of your solutions using the behavior of light to justify your answers. This explanation should include diagrams. 4. Hand in your group’s report and the Self-Evaluation Rubric. Resources: large plane mirrors, text, peer counsel, meter sticks, computer simulation at http://www.phy.ntnu.edu.tw/java/optics/mirror_e.html 1 CMSE Phys Lab Report Self-Evaluation Rubric Report Objectives “The report contains acceptable statements describing …” disagree unsure agree disagree unsure agree disagree unsure agree disagree unsure agree … the minimum length of a plane mirror that is needed for a person to see one’s full length image … the mirror’s precise placement on the wall in order to see a full length image … how the mirror’s size and placement depends on the height of the viewer … how the mirror’s size and placement depends on how far the viewer is from the mirror Report Objectives “The report contains acceptable explanations for …” … why the stated minimum mirror size is valid … why the stated mirror placement is valid … why the stated relationship about mirror size, placement, and viewer’s height is valid … why the stated relationship about mirror size, placement, and viewer’s distance from mirror is valid Report Objectives “The report contains correctly drawn and properly labeled ray di agrams that aid in the description and explanation of…” … why the stated minimum mirror size is valid … why the stated mirror placement is valid … why the stated relationship about mirror size, placement, and viewer’s height is valid … why the stated relationship about mirror size, placement, and viewer’s distance from mirror is valid Lab Objectives “Everyone in our lab group can now…” … give the minimum length of a plane mirror and its precise placement on the wall for a person of a given height to see a full length image when standing a designated distance in front of the mirror … justify why their response to the above is valid 2 CMSE Phys Plane M ir ror Imag es: P re-L ab P redi cti ons To be given out in class. 3 CMSE Phys Curved Mirror Ray Diagrams Calculate the image distance and size for each case. Enter these values in the data table. Using unlined paper in a landscape orientation, draw ray diagrams in order to find the image of each 2.0 cm object. Use a compass to accurately depict the curvature of each mirror. Label the focus “F” and center of curvature “C.” Draw three rays (through or toward focus and parallel, parallel and through or away from focus, and through the center of curvature) if possible. Measure the image size and distance. Record these values in the data table and compare with the calculated. On your diagrams, classify each image as 1) REAL or VIRTUAL, 2) UPRIGHT or INVERTED, and 3) REDUCED, ENLARGED, or SAME SIZE. Lens Concave Concave Concave Concave Concave Convex Convex Convex Convex Convex Object Distance 18.0 cm 12.0 cm 9.0 cm 6.0 cm 3.0 cm 15.0 cm 10.0 cm 7.0 cm 4.0 cm 1.0 cm Object size 2.0 cm 2.0 cm 2.0 cm 2.0 cm 2.0 cm 2.0 cm 2.0 cm 2.0 cm 2.0 cm 2.0 cm Focal Length 6.0 cm 6.0 cm 6.0 cm 6.0 cm 6.0 cm -5.0 cm -5.0 cm -5.0 cm -5.0 cm -5.0 cm Calculated di si Measured di si ***Notice that the focal length of a convex mirror is negative.*** CMSE Phys Measuring the Index of Refraction I. Glass/Plastic/Acrylic Rectangle and/or Triangle 1. Place the rectangle/triangle on the center of your paper. Trace around it. 2. Place one pin on either side of the object, snugly up against the sides. Rectangle: They should not be directly across from one another. Triangle: They should be directly across from one another. (Pins A and B in diagrams) 3. Look through the objects until these two pins line up in your eyesight. 4. Place another pin (C) between your eye and the two pins that are lined up in sight. Now all three pins (A, B, and C) should seem to be lined up. 5. Place a fourth pin (D) on the other side of the object in line with the other three. You should see all four pins lined up when you look through the object. 6. Remove the object and pins. 7. Connect the pin holes to show the path of light traveling through the rectangle/triangle. 8. With your ruler, carefully draw a dotted line “normal” to the object’s surface where the light ray enters the object. Draw another one where the light ray leaves the object. 9. Measure the angles of incidence and refraction where the light enters and where the light leaves the object. 10. Use Snell’s Law to calculate the index of refraction of your material. You will make this calculation for each set of angles. 11. Average the two values together. This is the material’s index of refraction. 12. Use the definition of the index of refraction to calculate the speed of light through the material. 13. Show all calculations on your ray diagram. 1 CMSE Phys II. Circular Water Dish 1. Place the circular water dish on the center of your paper. Trace around it. Carefully fill to near the top with water. 2. Place two pins on one side of the dish, one snugly against the side slightly off the center of the dish and the other directly in line with it. (Pins A and B in diagram) 3. Look through the dish until these two pins line up in your eyesight. Place another pin on the other side of the dish snugly against the side so that all three pins that are lined up in sight. (Pin C in diagram) 4. Place a fourth pin (Pin D) behind the dish in line with the other three. You should see all four pins lined up when you look through the dish. 5. Remove the water dish and pins. 6. Connect the pin holes to show the path of light traveling through the dish. 7. With your ruler, carefully draw a dotted line “normal” to the circular surface where the light ray enters the dish. Draw another one where the light ray leaves the dish. The normal will be a line through the center of the circular dish. 8. Measure the angles of incidence and refraction where the light enters and where the light leaves the dish. 9. Use Snell’s Law to calculate the index of refraction of the water. You will make this calculation for each set of angles. 10. Average the two values together. This is the water’s index of refraction. 11. Use the definition of the index of refraction to calculate the speed of light through the water. 12. Show all calculations on your ray diagram. 2 CMSE Phys Lens Ray Diagrams Calculate the image distance and size for each case. Enter these values in the data table. Using unlined paper in a landscape orientation, draw ray diagrams in order to find the image of each 2.0 cm object. Draw a double convex lens for the converging lenses and a double concave lens for the diverging. Label the focus F on each side of the lens. Draw three rays (through or toward focus and parallel, parallel and through or away from focus, and through optical center) if possible. Measure the image size and distance. Record these values in the data table and compare with the calculated. On your diagrams, classify each image as 1) REAL or VIRTUAL, 2) UPRIGHT or INVERTED, and 3) REDUCED, ENLARGED, or SAME SIZE. Lens Converging Converging Converging Converging Converging Diverging Diverging Diverging Diverging Diverging Object Distance 18.0 cm 12.0 cm 9.0 cm 6.0 cm 3.0 cm 15.0 cm 10.0 cm 7.0 cm 4.0 cm 1.0 cm Object size 2.0 cm 2.0 cm 2.0 cm 2.0 cm 2.0 cm 2.0 cm 2.0 cm 2.0 cm 2.0 cm 2.0 cm Focal Length 6.0 cm 6.0 cm 6.0 cm 6.0 cm 6.0 cm -5.0 cm -5.0 cm -5.0 cm -5.0 cm -5.0 cm Calculated di si Measured di si ***Notice that the focal length of a diverging lens is negative.*** CMSE Phys Images from Converging Lenses Learning Tasks: Complete and hand in one copy of the “PreLab Predictions” before picking up your equipment. Resources: converging lenses, candles, textbook, meter stick, computer simulation at http://www.schulphysik.de/suren/ CurvSurf/CurvSurf.html Part I: Blocking the Front of the Lens Use the available resources (candles, lenses, computer simulation, textbook, peer counsel) to answer the following questions: a) What happens to the image formed by a converging lens when the top half of the front side of the lens is covered? b) What happens to the image formed by a converging lens when the bottom half of the front side of the lens is covered? c) What happens to the image formed by a converging lens when a central portion of front side of the the lens is covered? d) What happens to the image formed by a converging lens as more and more of the front side of the lens is covered? 1 CMSE Phys Part II: Blocking the Back of the Lens Use the available resources (candles, lenses, computer simulation, textbook, peer counsel) to answer the following questions: a) What happens to the image formed by a converging lens when the top half of the back side of the lens is covered? b) What happens to the image formed by a converging lens when the bottom half of the back side of the lens is covered? c) What happens to the image formed by a converging lens when a central portion of back side of the the lens is covered? d) What happens to the image formed by a converging lens as more and more of the back side of the lens is covered? Part III: Blocking the Object Use the available resources (candles, lenses, computer simulation, textbook, peer counsel) to answer the following questions: a) What happens to the image formed by a converging lens when the top half of the object is covered? b) What happens to the image formed by a converging lens when the bottom half of the object is covered? c) What happens to the image formed by a converging lens when a central portion of the object is covered? d) What happens to the image formed by a converging lens as more and more of the object is covered? Develop an explanation of your answers using the behavior of light through lenses as justification. Write and hand in a complete and organized explanation that includes diagrams to justify your responses. 2 CMSE Phys PRELAB: Images from Converging Lenses Draw a sketch of what you think the image on the screen would look like when various portions of the lens/object are covered. Sketch in some rays traveling from the object to the screen that would form such an image. Part I: Blocking the Front of the Lens a) What happens to the image formed by a converging lens when the top half of the front side of the lens is covered? b) What happens to the image formed by a converging lens when the bottom half of the front side of the lens is covered? c) What happens to the image formed by a converging lens when a central portion of front side of the the lens is covered? Part II: Blocking the Back of the Lens a) What happens to the image formed by a converging lens when the top half of the back side of the lens is covered? 3 CMSE Phys b) What happens to the image formed by a converging lens when the bottom half of the back side of the lens is covered? c) What happens to the image formed by a converging lens when a central portion of back side of the the lens is covered? Part III: Blocking the Object a) What happens to the image formed by a converging lens when the top half of the object is covered? b) What happens to the image formed by a converging lens when the bottom half of the object is covered? c) What happens to the image formed by a converging lens when a central portion of the object is covered? . 4 CMSE Phys FUN WITH LIGHT AND COLO R Many students are taught in art classes that the 3 PRIMARY COLORS are: _______________, _______________, and _______________. From our own experiences with paint and/or crayons, we know that mixing different amounts of these 3 colors will produce other colors. For example, RED and YELLOW liquids combine to form _______________ liquid, RED and BLU E liquids combine to form _______________ liquid, BLU E and YELLO W liquids combine to form _______________ liquid, and BLU E, YELLO W, and RED liquids combine to form _______________ liquid. Many do not know that mixing colors of LIGHT is quite different from mixing colors of PAINT. To begin with, the 3 PRIMARY COLORS OF LIGHT are not red, blue, and yellow, but rather RED, BLU E, and GREEN . These 3 colors, or FREQUENCIES, of light combine in different ways than do colors of paint. Believe it or not, RED and G REEN light combine to form _______________ light, RED and BLU E light combine to form _______________ light, BLU E and GREEN light combine to form _______________ light, and BLU E, GREEN , and RED light combine to form _______________ light. Isaac Newton was perhaps the first person known to separate WHITE LIGHT into its component colors of ________, ________, ________, ________, ________, and ________. To do this, he used two PRISMS - one to separate light into its component colors, and the other to recombine them into white light. This method of separating light into its component colors uses the property of light known as REFRACTION. Another way to separate any light into its component colors is through properties of light known as DIFFRACTION and INTERFERENCE. A simple SPECTROSCOPE allows light to pass through a diffraction grating in such a way that the colors making up that light become known through these two processes. Learn more about mixing light and color by viewing these simulations on the World Wide Web: http://www.physicslessons.com/exp16b.htm http://www.physicslessons.com/exp18b.htm http://www.physicslessons.com/exp19b.htm 1 CMSE Phys MAKE YOUR OWN S PE CT ROS COPE Materials: hollow tube (paper towel roll, bamboo, toilet paper roll, etc…) , old compact disk, scissors, tape, card stock, exacto knife or razor blade, marker Procedure: 1. Place one end of your tube on the card stock and trace around the circle. (You may want to cut “flaps” around the disk for connection purposes.) 2. Use scissors to carefully cut this circle out of the card stock. 3. NOW USE THE RAZOR BLADE OR EXACTO KNIFE TO CAREFULLY CUT A NARROW VERTICAL SLIT IN THE CARD STOCK CIRCLE. This slit should be about 1-2 centimeters long and 1-2 millimeters wide. 4. Place this slit circle on one end of the tube and tape it into place. 5. Now place the other end of the tube on the compact disk and trace around the circle with the marker. 6. Use scissors to carefully cut this plastic circle out of the compact disk. 7. Use tape to pull the metallic covering off the top of the compact disk until it becomes totally transparent. 8. Place the compact disk circle on the other end of the tube and hold it into place. Do not tape it at this time. 9. While holding the tube so that the slit is vertically oriented, look through the compact disk end of the tube at a distant light. 10. Keep the slit circle vertical and rotate the compact disk circle until you see vertical color bands on both the right and left sides of the vertical slit. 11. Once you have it properly oriented, tape the compact disk end in place. 12. Look at various light sources and determine the colors of light comprising each source of light. Most incandescent and fluorescent bulbs contain all colors of the spectrum, but other gas-filled tubes contain only colors that are characteristic of the gases. Label each color of light seen when looking at a “white” light source. 2 CMSE Phys Electrical and Magnetic Properties Use the power supply, switch, wires, and light bulb to create a complete circuit that lights the bulb. Then check the electrical conductivity and magnetic attractiveness of each of your supplied materials. Object Conducts Electricity? Yes No Attracted to Magnet? Yes No On the back of this page, write some generalizations about: 1. conductivity and type of object 2. magnetic attraction and type of object 3. relationship, if any, between magnetic attraction and electrical conductivity CMSE Phys Ohm’s Law Objectives: • • • • • determine the conductivity of various materials set up a simple resistor circuit measure current through a resistor using an ammeter measure potential difference across a resistor using a voltmeter determine resistance and verify Ohm’s Law (i.e., R = V/I is constant) Materials: • D-cells and cell holders, multi-meters, wire, resistors, switch Procedure: • • • • • • • • • • Build a circuit to test the conductivity of materials in the bag. Test these materials and complete the chart. Draw both pictorial and schematic diagrams illustrating a circuit that includes the Ohm’s Law materials. Connect materials as shown in the diagrams. Record data from the multi-meters (used as a voltmeter and an ammeter) for six trials (using 1 - 6 cells in series) for each resistor. For each trial, divide “Potential Difference” by “Current” to obtain the “Resistance” for that trial (R = V/I). Average the trials for each resistor to obtain the “data table value” of resistance. Make a graph of “Potential Difference vs. Current” for each resistor. Include the origin (0,0) as a data point. Find the slope of the line that best fits your points. Enter this value as the “graph value” for the unknown resistance. Use the resistor color codes to determine the accepted resistance of each resistor. Compare your experimental value with the accepted value in a conclusion paragraph. Be sure to list sources of error in this activity. Pictorial Diagram Schematic Diagram 1 CMSE Phys Resistor I Color Bands - trial potential diff (V) current (Amps) resistance (Ω ) Average Resistance (Ω ) = Resistor II II Color Bands - trial potential diff (V) current (Amps) resistance (Ω ) Average Resistance (Ω ) = Resistor III I 0 0 - - I 0 0 - III I 0 0 - IV II II IV III V VI VII V VI VII VI VII - III Color Bands - trial potential diff (V) current (Amps) resistance (Ω ) Average Resistance (Ω ) = - IV V Analysis of Results resistor color code accepted value, Ω data table value, Ω % error graph value, Ω % error Conclusion: 2 CMSE Phys Light Bul bs in Seri es, P arall el, a nd C ombi nati on Each group must hand in their pre-lab predictions before obtaining the materials for this investigation. Learning Tasks: 1. Use the available resources (bulbs and circuit items, web-based circuit simulation, text, peer counsel) to determine what happens to the brightness of identical light bulbs in a dc circuit as more and more bulbs are a) added in series and b) added in parallel. 2. Develop a thorough explanation of why this occurs. 3. Use these same resources to develop an explanation of how one can determine the relative brightness of multiple bulbs when they are connected in combination circuits. 4. Hand in a complete explanation of your findings, containing multiple examples comparing the brightness of the bulbs in each type of circuit (series, parallel, and combination). Your explanation should include a method of how one may look at a schematic diagram of a combination circuit and be able to a) list the bulbs in order of increasing or decreasing brightness and b) tell which bulbs would be equally bright. Illustrate your method with two or more examples containing at least six bulbs in each of varying brightness. Resources: bulbs, wire, D cells, cell holders, multi- meters, textbook, peer counsel, computer simulation of a circuit found at http://www.physicslessons.com/exp22b.htm 1 CMSE Phys Light Bul bs in Seri es, P arall el, a nd C ombi nati on: Pre- Lab P redic tions 2 CMSE Physics Electrical Energy Costs The kilowatt-hour (kWh) is the basic unit of electrical energy used in determining one’s electrical utility costs. Since POWER = WORK /TIME (P = W/t), the kWh is actually a unit of WORK (W = P x T), or ENERGY, and is not a unit of power, as it is commonly believed and referred to. Therefore, one kWh (“kilo-Watt hour”) is equal to the total energy “consumed” (or “transferred”) by an electrical device with a power rating of one kilowatt during each hour of use. The electrical utility company will typically charge a home a set monthly rate for service plus an additional cost for each kWh used during the month. These rates vary by location, but generally fall between 5 and 10 cents ($0.05 - $0.10) per kWh. To find the total cost for using an electrical appliance in your home for one month, first find the number of kWh of energy used by multiplying its power (in kilowatts) by the total amount of time (in hours) used during the month. You may have to do some unit conversions to obtain this total. Then multiply this value by the cost per kWh to find the total cost. Procedure: I. Find the total monthly cost for using these devices, given the estimated times of usage. Assume a 30 day month and $0.075 per kWh. Appliance night light porch light radio microwave television central air clock hair dryer iron ceiling fan Power 5W 60 W 20 W 750 W 88 W 8200 W 10 W 1800 W 1200 W 12 W Usage 9 hr/night 12 hr/night 4 hr/day 30 min/day 6 hr/day 15 min/hr all day 5 min/day 4 hr/week 8 hr/day Total Time Total kWh Cost II. Make a chart similar to the one above and find out how much your family pays to use electrical devices each month by finding 15 (fifteen) examples in your own home. Be sure to make a realistic estimate of the actual amounts of time they are in use. Your 15 examples may include a maximum of 5 light fixtures or bulbs. Believe it or not, several students in the past have copied others work or just made up something to turn in and have missed the benefit of this assignment. Therefore, you must have this paper signed by a parent or guardian before handing it in to verify your own original work. “I verify that my child completed this assignment by finding actual examples in our home and doing his/her unique work.” Signature: _________________________________________ Date: ______________ CMSE Phys Electromagnet Strength Determine how the potential difference (voltage) applied to an electromagnet (with a fixed number of turns) affects its strength by comparing the applied potential difference to the electromagnet’s attraction to a force scale. # Turns of Wire # “D” Cells Electric Potential Difference, Volts Strength, N 1 2 3 4 5 6 Make a graph of Electromagnet Strength vs. Potential Difference. Include the origin as one of your data points. What does the shape of this graph indicate about the relationship between an electromagnet’s strength and its applied potential difference? Now use a fixed potential difference and vary the number of turns of wire to see how the number of turns of wire affects the strength of the elec tromagnet. # “D” Cells Electric Potential Difference, Volts # Turns of Wire Strength, N 4 4 4 4 4 4 Make a graph of Electromagnet Strength vs. # Turns of Wire. Include the origin as one of your data points. What does the shape of this graph indicate about the relationship between an electromagnet’s strength and its number of turns of wire? What would you need to do to make a really strong electromagnet? CMSE Phys FUN W ITH E LE CT RI CIT Y AND M AGNET ISM When a complete circuit is connected to a power supply, electric current, made up of extremely tiny particles (or waves, but that is another very long story) called electrons, flows through the wire and other circuit elements and transfer electric potential energy. This energy may be used to produce light, generate heat, and/or cause motion that we use in many products every day. Connect the circuit, throw the switch, and make the light bulb glow. Over 100 years ago, scientists discovered that when electric current flows through a wire, a magnetic field is produced around the wire. Open the switch, place a compass under the wire so that the wire lines up with the compass needle, and then close the switch. What do you notice? The deflection of the compass needle indicates the presence of a magnetic field around the current bearing wire. This knowledge soon led to practical applications of this phenomenon, including the construction of strong electromagnets that can be turned on and of at will, motors for converting electric energy into mechanical energy, and generators for converting mechanical energy into electric energy. A simple electric motor can be constructed in a very short time using common and inexpensive materials. To do this, a current-bearing loop of wire is constructed in a manner that causes the magnetic field from a nearby ceramic magnet to interact with the magnetic field surrounding the current-bearing wire loop and cause the loop of wire to spin. M AKE YOUR OWN DC EL EC TRI C MO TOR Materials: dry cell, small disk magnet, rubber band, 2 large paperclips, about 2 feet thin wire, nail, test tube or thick marker, scissors Procedure: 1. Take the 2 foot piece of thin wire and wrap it around the test tube (or thick marker). The number of wraps depends on the gauge (“thinkness”) of the wire. 2. “Tie” the ends of the wire through the loops so that the loop of wire will remain in place when you let go. 1 CMSE Phys 3. Bend the paper clips in order to form loops on their ends, which will be used for holding the wire loop. 4. Secure these to the dry cell with the rubber band. 5. Place the magnet on the dry cell and place the wire loop in its holders. Observe what happens. 6. Disappointed that nothing happened? The reason is that the wire is insulated with paint, which must be scraped off. This is the trickiest part. Whether or not the ends of the wire loop are scraped correctly will determine the success of your motor. 7. Hold the wire loop vertically between your thumb and index finger of one hand near the edge of the table (desk) so that the wire end lies on the table. 8. Use the other hand and the scissors to scrape the insulation off the top half of the wire. 9. Turn the wire loop around and scrape the top half of the other end. 10. Place the wire loop into its holders and move the loop so that it lies just above the magnet. The motor should now begin spinning. If not, you may need to give it a little push to get it going. Other instructions and pictures of electric motors made in similar ways may be found on the World Wide Web at: http://fly.hiwaay.net/~palmer/motor.html http://www.exploratorium.edu/snacks/stripped_down_motor.html http://www.scitoys.com/scitoys/scitoys/electro/electro.html#motor 2 CMSE Phys Simulated Radioactive Decay - Dice Instructions: 1. Complete the “Theoretical Decay” table entries by assuming that exactly 1/6 of all nuclei initially present decay each time period. Do this by taking 1/6 of the “initial number present” and round to the nearest whole number. Enter this number as the “number decayed.” 2. Subtract this value from the “initial number present” and record as the “number remaining.” 3. Repeat this process until the chart is complete or fewer than ten nuclei remain undecayed. 4. Make a graph of “Number of Radioactive Nuclei Present vs Time – Theoretical.” Draw a smooth curve through your data points. Now repeat this process using the dice to represent the unstable nuclei: 5. Begin with 300 dice. Toss the dice and remove each one showing the number ____________. The number you remove will be the “number decayed.” 6. Subtract the “number decayed” from the “initial number present” to obtain the “number remaining.” 7. Toss the remaining dice and again remove all those that “decay.” 8. Repeat this process until the chart is complete or fewer than ten dice remain. 9. Make a graph of “Number of Radioactive Nuclei Present vs Time – Experimental.” Draw a smooth curve through your data points. Discussion: a. Compare your “Theoretical Decay” chart and graph with the “Experimental Decay” chart and graph. b. Use the graph to estimate the amount of time necessary for your experimental number to go from 300 to 150 _____, 250 to 125 _____, 200 to 100 _____, 150 to 75 _____, and 100 to 50 _____. c. Based on your answers above, what is the approximate half-life of your “radioactive” sample? Extension: Repeat this decay simulation using more than one digit to represent a decayed nucleus and compare with the previous results. 1 CMSE Phys Data Table - Dice Elapsed Time 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 Dice: Theoretical Decay Initial Number Number Number Decayed Remaining Present 300 Dice: Experimental Decay Initial Number Number Number Decayed Remaining Present 300 2 CMSE Phys Simulated Radioactive Decay - Random Numbers Instructions: 1. Complete the “Theoretical Decay” table entries by assuming that exactly 1/10 of all nuclei initially present decay each time period. Do this by taking 1/10 of the “initial number present” and round to the nearest whole number. Enter this number as the “number decayed.” 2. Subtract this value from the “initial number present” and record as the “number remaining.” 3. Repeat this process until the chart is complete or fewer than ten nuclei remain undecayed. 4. Make a graph of “Number of Radioactive Nuclei Present vs Time – Theoretical.” Draw a smooth curve through your data points. Now repeat this process using the dice to represent the unstable nuclei: 5. Begin with 500 random digits. Choose the digit _____ and mark through each one of these. The number you mark out will be the “number decayed.” 6. Subtract the “number decayed” from the “initial number present” to obtain the “number remaining.” 7. Block out the remaining number of digits and again mark through all those that “decay.” 8. Repeat this process until the chart is complete or fewer than ten digits remain. 9. Make a graph of “Number of Radioactive Nuclei Present vs Time – Experimental.” Draw a smooth curve through your data points. Discussion: a. Compare your “Theoretical Decay” chart and graph with the “Experimental Decay” chart and graph. b. Use the graph to estimate the amount of time necessary for your experimental number to go from 500 to 250 _____, 400 to 200 _____, 300 to 150 _____, 200 to 100 _____, and 100 to 50 _____. c. Based on your answers above, what is the approximate half-life of your “radioactive” sample? Extension: Repeat this decay simulation using more than one digit to represent a decayed nucleus and compare with the previous results. 3 CMSE Phys Data Table - Random Numbers Random Numbers: Theoretical Decay Elapsed Time 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 Initial Number Present 500 Number Decayed Number Remaining Random Numbers: Experimental Decay Initial Number Present 500 Number Decayed Number Remaining 4 CMSE Phys Random Digits Chart http://www.rand.org/publications/classics/randomdigits/randomdata.html 00000 00001 00002 00003 00004 00005 00006 00007 00008 00009 00010 00011 00012 00013 00014 00015 00016 00017 00018 00019 00020 00021 00022 00023 00024 00025 00026 00027 00028 00029 00030 00031 00032 00033 00034 00035 00036 00037 00038 00039 00040 00041 00042 00043 00044 00045 00046 00047 00048 00049 00050 10097 37542 08422 99019 12807 66065 31060 85269 63573 73796 98520 11805 83452 88685 99594 65481 80124 74350 69916 09893 91499 80336 44104 12550 63606 61196 15474 94557 42481 23523 04493 00549 35963 59808 46058 32179 69234 19565 45155 94864 98086 33185 80951 79752 18633 74029 54178 11664 48324 69074 09188 32533 04805 68953 02529 99970 74717 10805 77602 32135 45753 17767 05431 99634 40200 67348 17674 35635 99817 26803 20505 14523 94598 81949 73742 49329 90446 45266 28573 16213 78317 52494 97654 15307 08391 85236 00597 61406 41430 14938 31994 24826 16232 00406 49140 32537 43902 45611 49883 77928 94138 20097 76520 64894 19645 09376 80157 34072 45571 02051 05325 03529 14905 39808 06288 86507 87517 17468 17727 77402 66252 14225 68479 26940 85157 11100 16505 26457 95270 67897 97344 73208 75246 64051 26898 45427 01390 87379 20117 01758 19476 36168 45240 41941 96382 71961 98145 77557 80993 52079 31249 87637 32825 13586 74296 09303 70715 36147 76850 82406 65692 47048 64778 68607 27732 98083 58401 64969 50950 08015 77214 29148 68514 27686 36858 47954 02040 34484 47774 79953 54387 08721 89837 33824 88159 09354 26842 92286 25241 45204 75379 07246 10851 28404 50949 70774 28296 06571 32270 37143 84827 64710 91976 39527 34673 24805 23209 38311 64032 36697 35303 68665 90553 35808 22109 50725 13746 36766 91826 58047 45318 43236 36936 46427 46162 70297 32979 12860 40219 51924 59367 54622 16868 68935 45862 96119 33351 83609 77281 05567 15956 40419 43667 34888 44999 89435 20151 69861 31010 97790 05335 59381 02295 35584 04220 54876 24037 02560 31165 36653 36170 42614 74818 57548 34282 40558 68248 70078 67951 08928 76974 22374 00210 87203 56788 83554 34135 26575 74697 52563 33729 83848 44431 48767 91416 51025 63896 35462 49700 44077 07007 60000 21585 94543 81553 08896 48581 23387 02591 24674 17119 12969 71539 36870 04401 86304 80959 20636 15953 88676 98951 65813 86799 73053 28468 60935 60970 29405 18475 90364 93785 73039 21115 45521 76621 96297 94750 53140 57600 96644 43651 65394 82396 91190 03071 26252 61962 54692 77974 13021 93910 86743 18743 66674 59047 01540 39094 88695 25016 74852 05455 52527 56127 09973 32307 10518 83389 09117 10402 34764 74397 16877 39885 07439 85247 28709 20344 93433 24201 40610 76493 61368 57186 78253 64237 13990 78822 89923 33340 40881 89439 77082 59593 10118 42592 12059 29663 79335 82391 50024 24892 83647 17157 92423 36806 90033 35456 73407 41994 25298 20539 61427 58021 19255 33440 57546 21615 87374 39292 00822 35080 04436 12171 11199 23403 18623 83491 35273 50500 52775 68711 29609 23478 40218 14385 96286 94400 54382 37089 42050 22222 28707 07207 42582 33211 92927 25701 05522 65337 23287 90103 78565 70617 85394 97118 84962 20826 05014 35441 37548 94624 00387 77938 80814 36040 88461 15020 01848 64278 74945 91665 33606 27659 76833 29170 09732 88579 25624 88435 73998 67851 77817 11062 34113 16544 53763 02655 56418 14598 20048 82341 06413 25815 31790 60527 59466 45973 46670 82562 12472 29529 39333 20106 42941 11838 96338 85207 69541 51176 31880 73043 61171 59579 91936 51748 90324 23356 09994 76938 58044 5 CMSE Phys 00051 00052 00053 00054 00055 00056 00057 00058 00059 00060 00061 00062 00063 00064 00065 00066 00067 00068 00069 00070 00071 00072 00073 00074 00075 00076 00077 00078 00079 00080 00081 00082 00083 00084 00085 00086 00087 00088 00089 00090 00091 00092 00093 00094 00095 00096 00097 00098 00099 00100 90045 73189 75768 54016 08358 28306 53840 91757 89415 77513 19502 21818 51474 99559 33713 85274 84133 56732 65138 38001 37402 97125 21826 73135 07638 60528 83596 10850 39820 59580 38508 30692 65443 27267 91307 68434 48908 06913 10455 12883 21778 19523 67245 60584 53853 24637 83080 16444 60790 03991 85497 50207 76490 44056 69910 03264 86233 53741 92694 03820 37174 59313 66499 68331 48007 86893 89640 16234 56806 02176 96397 40348 41134 42742 77929 83441 35655 62746 98952 06478 07341 70668 95659 50264 06991 94688 15877 45197 16019 97343 30976 59515 52670 47377 41377 38736 12451 24334 18157 10461 51981 47677 20971 66281 78542 81333 81594 61613 00397 86864 69979 93278 68107 62535 93584 11303 44035 17395 87648 81719 01304 87083 47143 95719 03061 07954 06958 99599 43622 75569 23793 94688 18288 13192 19072 84473 54745 42672 14210 65027 38807 65122 35583 07500 36066 74384 38992 36151 57178 93716 50654 26269 87749 31003 42785 10591 13628 62269 58391 29901 20288 81757 23621 24170 72869 22970 52166 96131 85261 11711 77586 31417 34072 09035 18072 19814 92983 10507 63147 78800 48763 16127 27437 72294 24210 13622 24591 78601 33712 61184 36961 59659 16563 37992 94850 89342 22815 99073 65762 16894 94938 62290 90429 00682 13661 40510 51215 50263 12607 68414 55210 05686 94049 69777 51926 28834 73852 10123 34313 71602 56271 21815 64638 85794 96207 59175 05128 13499 64421 88835 90822 56196 49632 07477 36699 62126 35700 11883 91342 04285 31649 86283 79246 45134 58838 52623 07759 27493 11161 66083 81997 64464 12272 27398 58873 07893 90290 90212 17646 82774 29773 73156 91345 12830 64721 34137 70091 91622 65861 92937 10086 39250 85902 74296 44156 20695 09719 06319 80814 54486 97022 80091 24041 44606 53728 98408 04754 09528 37821 01392 42096 68258 86686 26529 73859 07992 51777 70939 78576 24653 91870 27124 95375 20714 04618 32604 28466 55781 48949 51908 74287 07082 42836 74819 58303 73515 61222 85496 45875 74219 47324 75237 49139 08789 23821 05533 77433 53075 43800 23768 17719 82067 08337 17985 28825 12843 83824 63011 88325 17974 63281 69572 76463 26760 49364 12369 97377 85130 45819 84609 76150 67018 05871 53295 97553 60475 68795 76514 72306 13980 75251 85046 09191 78142 29822 90400 60561 57560 21069 64049 62605 62047 06441 88156 99538 52139 53783 71839 09351 06156 04207 63400 65676 48911 35793 82590 52692 98901 80851 15077 02023 13798 34222 83637 73331 18601 27585 32552 52979 58232 68476 41361 93823 07706 31223 94119 77762 83483 94541 72893 65344 31853 08007 43860 93174 71148 62327 81604 85644 65584 40030 15501 03856 64691 04713 61212 92301 06410 31024 04111 95954 05462 96299 97341 28976 09815 54130 14974 43667 90712 08816 16435 26655 41326 96240 03742 51972 54846 65130 88618 64659 82760 43178 17813 08420 01840 20791 47055 37408 55507 67415 38452 45449 72834 93972 43643 18423 18880 47277 49698 37438 29578 54552 19202 66994 06455 50498 19362 73167 08408 49953 69200 90836 30358 66252 93146 55160 40344 70883 26769 47449 91529 90802 44344 43642 83873 37867 54759 04860 19161 6 CMSE Phys 7 CMSE Phys 8