* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download - Office Mix
Golden ratio wikipedia , lookup
Perceived visual angle wikipedia , lookup
History of trigonometry wikipedia , lookup
Euclidean geometry wikipedia , lookup
Rational trigonometry wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Trigonometric functions wikipedia , lookup
Incircle and excircles of a triangle wikipedia , lookup
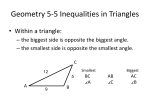
Triangle Inequalities Objective • I CAN discover the Triangle Inequality Theorem and apply inequalities in one triangle. The DHS Chick-Fil-A Run x The DHS Football team is headed to M&T Bank stadium for the state playoffs. The game isn’t until 7 PM, so they decide to stop for Chick-Fil-A on the way there. A few players don’t want to stop, and head straight for the stadium. Which of the following is a possible distance from DHS to M&T Bank Stadium? 25 6 12 18 20 16 Triangle Sides • If one side of a triangle is longer than another side, then the angle opposite the longer side has a greater measure than the angle opposite the shorter side. B 5 9 C A 7 Examples • List the Angles from largest to smallest Largest P Largest C Medium M Medium B Smallest N Smallest A Triangle Angles • If one angle of a triangle has a greater measure than another angle, then the side opposite the greater angle is longer than the side opposite the lesser angle. E 77° 65° D 38° F Examples • List the sides of triangle from largest to smallest Largest QS Largest CB Medium QR Medium CA Smallest RS Smallest AB Triangle Inequality Theorem • The sum of the lengths of any two sides of a triangle is greater than the length of the third side. Example • Do these numbers represent a triangle? 1.) 9, 7, 12 2.) 5, 5, 10 3.) 1, 4, 6 4.) 6, 6, 2 Finding Range of Third Side • If you are given two sides of a triangle you can determine the range that the third side must fall in.