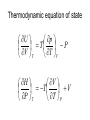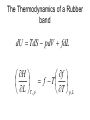* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture VIII_IX
Thermal conduction wikipedia , lookup
Van der Waals equation wikipedia , lookup
First law of thermodynamics wikipedia , lookup
Conservation of energy wikipedia , lookup
Temperature wikipedia , lookup
Equation of state wikipedia , lookup
Non-equilibrium thermodynamics wikipedia , lookup
Heat transfer physics wikipedia , lookup
Internal energy wikipedia , lookup
Chemical thermodynamics wikipedia , lookup
Maximum entropy thermodynamics wikipedia , lookup
History of thermodynamics wikipedia , lookup
Entropy in thermodynamics and information theory wikipedia , lookup
Thermodynamic system wikipedia , lookup
Second law of thermodynamics wikipedia , lookup
Adiabatic process wikipedia , lookup
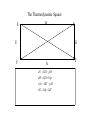
Entropy changes in irreversible Processes To obtain the change in entropy in an irreversible process we have to calculate DS along a reversible path between the initial state and the final state. Freezing of water below its freezing point H2O( l , -10 °C) Irrev H2O( s , -10 °C) H2O( s , 0 °C) H2O( l , 0°C) DS Cliq ln 273 DH crys 263 Cice 263 T 273 A sample of 1.00 mole of monoatomic perfect gas with Cv,m = 1.5 R, initially at 298 K and 10 L, is expanded, with the surroundings maintained at 298 K, to a final volume of 20 L, in three ways (a) isothermally and reversibly (b) isothermally against a constant external pressure of 0.5 atm (c) adiabatically against a constant external pressure of 0.5 atm . Calculate ΔS and ΔSsurr, ΔH and ΔT for every path. Question? • A 50 gm mass of Cu at a temperature of 393 K is placed in contact with a 100 g mass of Cu at a temperature of 303 K in a thermally insulated container. Calculate q and ΔStotal for the reversible process. Use a value of 0.4184 Jg-1K-1 for specific heat capacity of Cu. Absolute entropy of a substance S (T ) S (0) Tf 0 Tb Tf C p ( s ) dT T C p (l ) dT T T C p ( g ) dT Tb T D f H Tf Dv H Tb Third law of thermodynamics: The entropy of each pure element or substance in a perfectly crystalline form is zero at absolute zero. Spontaneous process dS sys dS surr 0 dS sys dS surr dq T dq TdS 0 At constant v olume, no additional dqv TdS 0 dS sys dU TdS 0 dSU ,V 0 or dU S ,V 0 At constant V and T dU TdS dU d (TS ) d (U TS )V ,T 0 d ( A)V ,T 0 A is called helmholtz free energy. work dS sys dS surr 0 dS sys dS surr dq T dq TdS 0 At constant pressure, no additional work dS sys dq p TdS 0 dH TdS 0 dS H , p 0 or dH S , p 0 At constant P and T dH TdS dH d (TS ) d ( H TS ) P ,T 0 d (G ) P ,T 0 G is called Gibb' s free energy. Enthalpy/ Entropy driven process A-Enthalpy driven B-Entropy driven Hydrophobic Effect in Protein Folding DS=+ + HOH HOH Folded More Hydrocarbon-Water Interfacial Area Unfolded Less Hydrocarbon-Water Interfacial Area Hydrophobic forces • Hydrophobic interactions are considered to make a major contribution to stabilizing the native structures of proteins in aqueous environment. • The hydrophobic effect is a unique organizing force based on repulsion by the solvent instead of attractive forces at the site of organization. • Thermodynamics of protein unfolding can be explained on the basis of transfer of non-polar groups from organic solvent to water. Enthalpy and Entropy DGo = DHo - TDSo •Typically, DG and DH are measurable and DS calculated •DH and DS Provide Mechanistic Insight •In very rough generalities: DH related to bond formation/breaking DS related to configurational freedom and water ordering •dDH = DCpdT Gives Thermal Dependence of K Reason for negative DS H O H O H H Water molecules seek favorable positions and partially freeze their thermal motion. Hydrophobic bond Extreme ordering of waters caused by hydrophobic molecule • Net effect is entropic rather than energetic in nature just because the energy of H-bonds is extremely high and waters would prefer to become frozen and sacrifice a part of their freedom than to lose the large energy of a hydrogen bond. A simple binding process Binding can be enthalpy or entropy driven + + Enthalpic contribution to Free energy of binding • Ionic and hydrogen bonds. • Electrostatic interaction. • Van der Waal interaction entropy of binding • Binding is favoured if it leads to a net increase in disorder or entropy. • This includes entropy of – the system (interacting molecules and solvent) • represented as change in entropy or DS – the environment (everything else) • as the system releases or absorbs heat it changes the entropy of the surroundings • heat release is measured as change in enthalpy or DH Combining the First and Second law dU TdS pdV U f (S ,V ) U U T p S V V s T p V s S V dH dU pdV Vdp dH TdS pdV pdV Vdp dH TdS Vdp H T S p H V p S T V S p p s H S U P G V A S p V T T V S V T p p T T V p s S p T p V s S V T Good people have studied under very able teachers. dA d U TS dA dU TdS SdT dA TdS pdV TdS SdT dA SdT pdV S p V T T V dG dH TdS SdT dG TdS Vdp TdS SdT dG Vdp SdT S V T p p T The Thermodynamic Square S H U V P G A dU TdS pdV dH TdS Vdp dA SdT pdV dG Vdp SdT T Thermodynamic equation of state U p T P V T T V H V T V P T T P U V T Prove it V CP T 2 P T T P 2 Derive the expression for for a gas following the virial equation with Z=1+B/V True or False ?? No heat transfer occurs when liquid water is reversibly and isothermally compressed. During an adiabatic, reversible process at constant volume the internal energy can never increase. The internal energy of a system and its surroundings is never conserved during an irreversible process, but is conserved for reversible processes. The work done by a closed system can exceed the decrease in the system’s internal energy When extra (useful) work is involved. Important Thermodynamic equations dU TdS pdV dwe dH TdS Vdp dwe dS sys dS surr 0 dA SdT pdV dwe d (G ) P ,T 0 dG Vdp SdT dwe Helmholtz free energy dS sys dS surr 0 dS sys dS surr dq T dq TdS 0 For Reversible process dU dw TdS 0 dw dU TdS dwmax dU TdS dA (At constant Temperatur e) dS sys Maximum work done (including expansion work) can be calculated by measuring the change in A. Gibb’s Free Energy In the presence of extra work, dG -SdT VdP dw add, rev At constant t emperature and pressure, dG dwadd ,rev E.M.F. work dG SdT pdV dwe DG P ,T 0 dGP ,T dwe nFdE nFDE P ,T 0 DGP ,T nFDE DE P ,T 0 Displacement of metal from metal salts • A more active metal can "displace" a less active one from a solution of its salt. • “Active" metals are all "attacked by acids“. • Zn(s) + Cu2+ → Zn2+ + Cu(s) . DE P ,T ve 1.09V Pressure as a function of height • An increase in height will correspond to a decrease in pressure. • Boiling point of water is raised if the pressure above water is increased; it is lowered if the pressure is reduced. This explains why water boils at 70 °C up in the Himalaya. DG SdT VdP mgdh DGT VdP mgdh At equilibriu m VdP mgdh dP gdh PM dP gdh RT dP Mg dh P RT P ln 2 P1 Mg (h1 h2 ) RT The Thermodynamics of a Rubber band dU TdS pdV fdL f H f T T p , L L T , p • Q.Experiments show that the retractive force f of polymeric elastomers as a function of temperature and expansion L is given by f(T,L) = aT(L-L0) where a and L0 are constants. • (a)Use Maxwell relations to determine the entropy and enthalpy at constant T and p. • (b) If you adiabatically stretch a rubber band by small amount, its temperature increases but volume does not change. Derive an expression for its temperature as a function of L, L0, a and C (heat capacity). The variation of Gibb’s energy with temperature. H G / T 2 T T Variation of the Gibb’s energy with pressure dG Vdp SdT At constant t emperature , dG Vdp (a) Liquids and solids Vm constant DGm V p2 p1 (b)Gases Ideal Gas DGm pi p pf RT dp RT ln p pi (standard pressure at 1 bar) DGm RT ln pf p Question ? • Calculate ΔG for the conversion of 3 mol of liquid benzene at 80 C (normal boiling point) to vapour at same temperature and a pressure of 0.66 bar? Consider the vapour as an ideal gas. • In the transition CaCO3 (aragonite) to CaCO3 (calcite), ΔGm (298) = -800 J and DVm = 2.75 cm3. At what pressure would aragonite become the stable form at 298 K?.