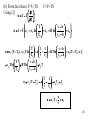Download The Helmholtz Function

Chapter 8
Thermodynamic Potentials
1
Now that we have the 1st and 2nd Laws of thermodynamics, you
might think that we can now apply these laws to many different
situations using the concepts of internal energy and entropy.
Although this is possible, it is very helpful to introduce three other
state variables with the dimensions of energy. We have already
made our acquaintance with one of them, the enthalpy. In this
chapter we introduce two other concepts which have wide use.
2
In this chapter we introduce thermodynamic potentials. There is
a fundamental set of four, all of which are energies and hence
conserved. They are:
U the internal energy
H enthalpy ( old fashioned name is “heat content”)
Important when discussing heat capacities and latent
heats.
F Helmholtz Function. Often A is used as the symbol.
Important in statistical mechanics
G Gibbs Function. Important in phase transitions and
chemical reactions.
The thermodynamic potentials are also called generating functions.
These potentials, similar to potential energy in mechanics, are
introduced for convenience in the analysis of certain processes.
3
• Legendre Transformation
This is a very useful mathematical transformation.
For example it is used in classical mechanics to go
from the Lagrangian to the Hamiltonian.
One often introduces the notion of canonically
conjugate pairs, one variable being extensive and
the other intensive. For example (V, -P), (S, T).
In an analysis of certain processes U is often not a
convenient function to work with. We have already
introduced another useful function (H) and now we
will introduce two new state functions:
 Helmholtz F
 Gibbs
G
4
The thermodynamic potentials U, H, F and G are
state functions. If we know these functions then all
the thermodynamic properties of a system can be
calculated by differentiation alone.
Consider dU(S,V) = TdS - PdV
The extensive variables S,V are taken as
independent. We say that U is a generating function
having as its natural variables S and V. Canonically
conjugate pairs are (-P, V) and (T, S). The first pair
are mechanical variables and the second pair are
thermal variables.
5
We have
dU(S,V) = TdS - PdV
But we can write dU   US V dS   UV S dV
Comparing gives
 US V  T
and
 UV S   P
These two equations are called the equations of state.
Hence if we know U(S,V) we can obtain T and P by
differentiation.
There are four possible pairings of a thermal variable and
a mechanical variable:
(S, V) (S, P) (T, V) (T, P)
We will obtain thermodynamic potentials for each of
these pairs. This will be done using a Legendre
Transformation.
6
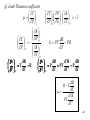
Consider Z = Z(x, y)
dZ = Xdx + Ydy _ _ _ _(1)
with (x, X) and (y, Y) as canonical pairs. Suppose
we wish to replace (x, y) by (X, Y). We use a
transformation to form a new function
M(X, Y) = Z - xX - yY
dM = dZ - Xdx - Ydy - xdX - ydY
dM = - xdX - ydY _ _ _ _(2)
 Z 
 Z 
dZ    dx    dy
 x  y
 y  x
 M 
 M 
 dX  
 dY
dM  
 X Y
 Y  X
The reciprocity relations are:
 Zx y  X
 MX Y   x
 
Z
y x
Y
 MY X
 y
7
To replace only one variable, say y by Y:
N(x,Y) = Z - yY _ _ _ _(3)
and using (1) dN = Xdx - ydY _ _ _ _(4)
 N 
 N 
dN  
 dx  
 dY
 x Y
 Y  x
with reciprocity relations
 Nx Y  X
 NY x   y
With this introduction we proceed to the thermodynamic
potentials.
8
Definition of the Thermodynamic Potentials
We had, for the first law of thermodynamics, for a
hydrostatic system:
dU(S, V) = TdS - PdV _ _ _ _(5)
We will replace U(S, V) by a new state function H (S,
P) (natural variables). In this case we are replacing
only one variable V by its conjugate -P.
H=U-(-P)V →
H=U+PV
dH=dU+PdV+VdP
dH=TdS-PdV+PdV+VdP → dH=TdS+VdP
 H 
 H 
 dS  
 dP
dH  
 S  P
 P  S
9
Reciprocity relations:
 HS P  T
 HP S  V
If H is written in terms of S and P differentiation permits
us to calculate T and V.
10
The Helmholtz Function
Now we wish to replace U(S, V) by F(T, V)
We wish to replace S by T. The appropriate Legendre
transformation is then F(V,T)=U-ST
dF=dU-SdT-TdS=TdS-PdV-SdT-TdS
dF(V,T) = -PdV – SdT
 F 
 F 
 dT  
 dV
dF  
 T V
 V T
 
F
V T
 P
 
F
T V
 S
Again, if F is a known function of V and T (natural
variables), then we can obtain P and S.
11
The Gibbs Function
Now we wish to replace U(S, V) by G(T, P).
Two variables are changed so we use
G(T, P) = U – ST + VP giving
dG(T, P) = -SdT + VdP
 GT P  S
 GP T  V
Let us summarize the thermodynamic potential
functions.
dU(S,V) = -PdV + TdS _ _ _ _(a)
dH(S,P) = VdP + TdS _ _ _ _(b)
dF(T,V) = -PdV – SdT _ _ _ _(c)
dG(T,P) = VdP – SdT _ _ _ _(d)
12
Helmholtz Function
In statistical mechanics the quantity that is usually
calculated is the Helmholtz Function. Other
thermodynamic properties are then calculated
from this.
Before pursuing a general discussion of this function,
let us consider a example to show how U and F differ by
means of a simple example. We consider a closed cylinder
in which there is a piston which separates two gases which
as not initially at the same pressure. The situation is shown
on the next slide.
13
Bath at T
V1
V2
Cylinder
Piston (adiabatic)
We let the piston move until equilibrium is achieved.
Now we consider an infinitesimal reversible change about this
equilibrium position.
(a) Suppose that the wall of the cylinder is adiabatic.
đ Q  dU  PdV đ Q  0
dU   PdV
dU  dU 1  dU 2   P1dV1  P2 dV2
Since the pressures are now the same and obviously dV2  dV1
we have dU=0. At equilibrium the internal energy has
its minimum value.
14
(b) Suppose that the wall of the cylinder is diathermal.
dF  SdT  PdV
dT  0 dF  PdV
dF  dF1  dF2  P1dV1  P2dV2
Since the pressures are now the same and dV2  dV1
we have dF=0. In this situation, it is F, not U that is a minimum
at equilibrium.
(U is not minimized in this case because the total entropy of the
system and the reservoir must be maximized and the Helmholtz
Function takes this into account.)
In continuing our discussion of the Helmholtz Potential, we
consider isothermal processes.
{As an aside we have (slide 11)
 
F
V T
 P
}
15
Recall that if we have a system in contact with a reservoir
(surroundings at constant temperature) then
S (system) + S (reservoir)  0.
If an amount of heat Q is transferred from the reservoir to the
system, then
(at T)
S(system) - Q  0 giving
T
Q  T (S) (system)
The equality sign holds only for a reversible process. We have
F= U – ST (This is just the Legendre Transformation.)
At constant temperature: F = U - TS or
F = Q - W - TS
16
If no new entropy is created in a process (reversible process) then
Q = TS and F = -W or
( F f  Fi )  W (constant T)
The change in the Helmholtz function is then equal to the work
done. If new entropy is created in a process (irreversible) then
Q <TS and F < -W or
( F f  Fi )   W (constant T)
The work is all the work on or by the system, including any done
by the system’s surroundings.
Conclusion:
If a system undergoes a reversible process at constant T and V (no
work) then the Helmholtz Function does not change.
If the system undergoes an irreversible process under constant T
and V, then the Helmholtz Function decreases.
17
Conclusion:
The change in F in an isothermal reversible process is the work done
on or by the system. In an isothermal process, the maximum
amount of work that can be done by a system is the decrease in the
Helmholtz function.
W  Fi  F f (constant T)
One can also say that the decrease in F gives the maximum amount of
energy that can be fixed in an isothermal process and made available
for work. (The symbol A is often used for the Helmholtz function.
Arbeit is German for work). For this reason F is often called the
Helmholtz free energy.
So F is intimately associated with work in an isothermal process.
(See slide 22 for an example.)
18
If we consider constant T and constant V and
no other types of work, W = 0 and F  0
and so (Ff - Fi) < 0 in an irreversible process.
Natural processes at constant T and V undergoing
change will move to lower values of F.
Equilibrium occurs at minimum F.
The Helmholtz potential is a function of T and V,
its natural variables. In statistical mechanics these
are the important variables, hence the importance
of the Helmholtz potential in statistical
mechanics.
The example starting on the next slide is to show that, if the
Helmholtz Function is known, many other thermodynamic
properties can be calculated.
19
Example: Some expressions involving F(T,V).
We previously obtained the expressions:
 
F
V T
 P
F  U  TS
 
F
T V
 TS  F  U
 S
H  U  PV
G  H  TS  (U  PV )  ( F  U )  F  PV
 F 

G  F  V 
 V T
U  F  TS
H  U  PV
 F 

U  F  T 
 T V
 F 
 F 
  V 

H  F  T 
 T V
 V T
20
 U 
CV  

 T  V
and we had
 F 
U  F  T

 T  V
2

F

F

F

 


CV     
  T 2 
 T  V  T  V
 T  V
 F
C V   T 2 
 T  V
2
Notice that the thermodynamic quantities are all expressed as
functions of
 F   F 
 , 

F ,V , T , 
 T V  V T
If one can theoretically calculate F(V,T) then any other
thermodynamic function can be obtained as a function of V and T.21
EXAMPLE: A cylinder contains a piston on each side of which is one
kilomole of an ideal gas. The walls of the cylinder are diathermal and
the system is in contact with a heat reservoir at T=273K. The initial
volumes of the gases are 12 liters (left) and 2 liters (right). The piston
is now moved reversibly so that the final volume on both sides is 7
liters. What is the change in the Helmholtz potential?
f
12
dF=-PdV-SdT=-PdV
2
F    PdV
i
1 kmole
Since we have 1 kmole of each gas
PV=RT and T is constant.
7
For the left side: Wl  RT dV  RT ln 7 
 

1 kmole
273K
 12 
7
 7
dV
Wr  RT 
 RT ln 
V
2
2
12 
7
7
1 kmole 1 kmole
For the right side
V
 7 7
 49 
J
F   RT ln
   8.314  103 (273 K ) ln 
K
 12 2 
 24 
(Some work is done and
F decreases.)
F  1.62MJ
22
EXAMPLE (Problem 8.5): The Helmholtz function for a certain gas is:
n 2a
F( V , T )  
 nRT ln( V  nb )  J(T)
V
Obtain an expression for the pressure of the gas.
We have the reciprocity relation
 1 
n2 a

 P  2  nRT 
V
 V  nb 
 1 
n2 a

P  2  nRT 
V
 V  nb 
 F 

   P
 V T
n2 a
nRT
P 2 
V  nb
V

n2 a 
 P  2 (V  nb)  nRT


V


Placing in a form using the specific volume:
a 

 P  2 ( v  b)  RT
v 

Van der Waals gas
(The reciprocity relationship has led
to the equation of state.)
23
EXAMPLE: A van der Waals gas undergoes an isothermal expansion
from some initial specific volume to a final specific volume. Calculate
the change in the specific Helmholtz function.
We have
dF   PdV  SdT   PdV df   Pd v
a 

 P  2 ( v  b)  RT
v 

 RT  a 
 f    
  2 dv
vb v 
v 1 
v2
 v2  b   1
1 
  a
f   RT ln
 
 v1  b   v 2 v1 
(Again the Helmholtz thermodynamic potential is closely
associated with the work done in an isothermal process.)
24
EXAMPLE: The molar value for F for a gas is given by
 T 1 1 
 vb 
  s 0 (T  T0 )  f0
f  c V (T  T0 )  c V T ln   a    RT ln
 T0   v v 0 
 v0  b 
(a) Derive the equation of state.
(b) Derive the energy equation.
(a) From slide 12 (or from fact sheet)
df=-Pdv-sdT
 f 
 f 
f ( v , T)  
 dT    dv
 T  V
 v  T
 f 
(reciprocity relations)
P    ......(1)
 v  T
From (1) P    a  RT  P   a  RT
 2

2
v
v  b
v
vb
so
 f 
s  
 ......( 2)
 T  v
a 

 P  2 ( v  b)  RT
v 

25
(b) From fact sheet F=U-TS
Using (2)
 f 
U=F+TS
u  f  T

 T  V


T
 vb 
  s 0 
u  f  Tc V  c V ln    c V  R ln 
 T0 
 v0  b 


 T 1 1 
 vb 
  s 0 (T  T0 )  f 0
u  c V (T  T0 )  c V T ln   a    RT ln
 T0   v v 0 
 v0  b 
T
 vb 


  s 0 T
 c V T ln   RT ln
 T0 
 v0  b 
1 1 
u  c V (T  T0 )  a    s 0T0  f 0
 v v0 
u  cVT 
a
 u0
v
26
• Gibbs Function (very important in chemistry)
G = H – TS
To create a system one need not supply the entire
enthalpy, as some energy (TS) can flow in as heat
from the surroundings. Only the difference (H-TS)
must be supplied by work.
(See example on slide 34.)
Consider a system in surroundings that constitute a
T and P reservoir. This is the usual environment
for chemical reactions and some phase changes. (T
and P natural variables for the Gibbs Function.)
Since H = U + PV
G = U - TS + PV
27
Considering a process which is both isothermal and
isobaric G = U - TS + PV and since
U = Q - W, then
G = Q - W - TS + PV
In general, besides any mechanical work, we can
have some other work, such as electrical work.
W = PV + W(other)
G = Q - TS -W(other)
Suppose W(other) = 0
As before Q  TS and so G  0 for constant T, P.
Again, in an evolving process, equilibrium will be
established when G reaches its minimum value.
28
Suppose W (other) 0
If we have a reversible process Q = TS and
G = -W(other), so
W(other)  (Gi  Gf )
Gf - Gi = -W (other) or
The change in the Gibbs function gives the maximum
energy that can be freed in an isothermal, isobaric
process and made available for non-mechanical work.
For this reason one often speaks of the Gibbs free
energy. This can be confusing as we have the
Helmholtz free energy also. It is best to avoid using
free in both cases.
N.B. The state variables T and P need not be fixed
throughout the process, but must have the same initial
and final values.
29
Reversible processes: Let us summarize some results
for some particular reversible processes.
Isochoric
Isobaric
Isothermal
Isothermal, isobaric
dU = đQ
dH = đQ
dF = -đW
dG = -đW(other)
30
Finally let us consider a change in phase
(sublimation, fusion and vaporization) that takes
place isothermally and isobarically. No work (other)
is involved and so, in a reversible process, G = 0 or
G = constant. We use g to indicate the molar Gibbs
function.
Notation: g' = saturated solid
g" = saturated liquid
g"' = saturated vapor
Equation for fusion curve
is g' = g"
Equation for vaporization curve is g" = g"'
Equation for sublimation curve is g' = g"'
At the triple point g' = g" = g"'
[Note: saturated means that the state of the system is at one
of the phase transformation (or coexistence) curves on a
P-T diagram.]
31
The quantity G is tabulated for a variety
of chemical reactions and other processes.
G = H - TS
In most work we do not need to choose a
reference point as, usually, only changes in
the quantities are of interest.
{One source of tabulations of thermodynamic properties
is the CRC Handbook of Chemistry and Physics.}
32
The relationship amongst the thermodynamic
potentials can be summarized as follows:
- TS
U
F
H
G
+ PV
33
1
EXAMPLE: Electrolysis of 1 mole of water. H2O  H2  O2
2
1 mle 1 mle+0.5 mle
Process takes place at P=1 atm. and T=298K
From a table we find that the change in enthalpy required for this
phase change is H  286 kJ
Some data (for 1 mole): S H2O  70
J
K
S H2  131
J
K
SO2  205
J
K
The enthalpy must be supplied in some fashion. Must all of this
energy be supplied by work or can some enter from the environment
as heat? Considering some reversible process and since it is
isothermal and isobaric: H  G  TS
But G  W (other)  W (electrical )
H   W(electrical )  TS (1)

J
205
J
S  S f  Si  131 
 70   163
2
K

K
34
Since T=298K TS  49 kJ
This increase in entropy is due to energy coming into the system by
means of the heating process. (Note that the volume increases.)
The electrical work that must be performed is, from equation (1):
H  TS   W(electrical )
286 kJ  49 kJ  237 kJ   W(electrical )
The – sign indicates that work must be done on the system
The gas must push the environment aside. We obtain the work done by
the gas by assuming an ideal gas (neglect the volume of the water)



1
J
(298 K )  4 kJ
PV  nRT  1 mole  mole  8.31
2
mole  K 


So, of the total energy supplied (237+49)kJ=286kJ, (286-4)kJ=282kJ
goes into an increase in the internal energy of the system.
35
{Or G=U-TS+PV
U  G  PV  TS
}
PV  4kJ
237kJ
(electrical energy)
U  282 kJ
SYSTEM
49kJ
(heat)
36
Fuel Cell. If one combines hydrogen and oxygen to produce water
in a controlled way one can extract, in principle, 237 kJ of electrical
work for each mole of hydrogen. This is the principle of the fuel cell.
This is the reverse of the process that we have just examined.
49 kJ of energy is expelled as waste heat. A reasonable measure of
the efficiency is

W (electrical )
U  PV ( gas)

237
 0.83
282  4
In practice, the efficiency will be somewhat less, but still better than
a heat engine.
{Where do the hydrogen and oxygen gases come from?)
37
EXAMPLE: The specific Gibb’s potential of a gas is given by:
P
g  RT ln   BP with B  B(T )
 P0 
(Natural
Derive everything. Express answers in terms of P and T variables)
(a) Equation of state
 g 
 g 
dg  sdT  vdP dg  
 dT  
 dP
 T  P
 P  T
giving
 g 
s  
 .....(1)
 T  P
From (2)
RT
v
B
P
(reciprocity
 g 
v
.....(
2
)

relations)
 P  T
P( v  B)  RT
(b) Specific entropy
From (1)

P
dB 
s    R ln    P


 P0 
dT 

P
dB 
s   R ln    P

P
dT


 0
38
(c) Helmholtz potential
g  f  Pv
RT
v
B
P
(d) enthalpy
f  g  Pv
P
f  RT ln   BP  Pv
 P0 
P
f  RT ln    BP  RT  PB
 P0 
 P 
f  RTln    1
  P0  
P
P
 dB 


g  h  Ts h  g  Ts  RT ln   BP  RT ln   PT

P
P
dT


 0
 0
 dB 

h   BP  PT 
 dT 
(e) Internal energy
f  u  Ts
 P


P


u  RT ln    1  T  R ln   
  P0 


 P0 
  dB 

  B
h  P T 
  dT 

u  f  Ts
P
P
 dB 
 dB 


  RT ln    RT  RT ln    PT 

P
dT
P
P
dT




 0
 0
u   RT  PT
dB
dT
 dB

u  T P
 R
 dT

39
(f) Specific heat at constant pressure
 dB
 h 
d 2 B dB 
cP   
cP  P 
T


2

T
dT
dT
dT
 P


d2B
cP  PT
dT 2
(g) Specific heat at constant volume
 u 
cV  

 T  V
 RT dB

RT2 dB
 dB

u  TP
 R   T
 R 
 RT
 dT

 ( v  B ) dT
 ( v  B ) dT
2RT dB
RT2 d 2B
1
dB
2 dB
cV 


RT
R
2
2
( v  B) dT ( v  B) dT
dT ( v  B) dT
!
2
dB P 2 ( v  B ) 2 d 2 B
RT2  dB 
c V  2P


 R
2
2 
dT
R( v  B ) dT
( v  B )  dT 
c V  2P
2
dB 1 2
d B P  dB 
 P ( v  B) 2 

 R
dT R
dT
R  dT 
2
cV  2 P
2
2
dB
d B P  dB 

  R
 PT

2
dT
R  dT 
dT
2
2
40
(h) Isothermal compressibility
1  v 
RT  v 
RT
 
v  B 


  2
v  P  T
P  P  T
P
1 RT

v P2
RT

P( RT  PB )
(i) Volume expansivity
1  v 
 

v  T  P
RT
R dB
 v 
v
B 
  
P
 T  P P dT

RP
Pv
dB
dT
1  R dB 
  
v  P dT 
dB
dT

RT  PB
RP
41
(j) Joule-Thomson coefficient
 T 
   
 P  h
 T 
 
 P  h
dB
 h 
  T
dT
 P  T
 T   P   h 

   
  1
 P  h  h T  T  P
 h 
 
P T
dB


h  PT
 PB
dT
 h 
 
 T  P
2

h
dB
d
B
dB


B
 PT 2  P

 P
dT
dT
dT
 T  P
dB
dT

d2B
PT
dT 2
B T
42
• Maxwell’s Relations
Let us apply the condition for an exact
differential to the differential forms of the
potentials.
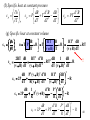
dU = TdS - PdV
dH = TdS + VdP
dF = - SdT - PdV
dG = -SdT + VdP
 VT S   PS V
 TP S   VS P
 VS T   TP V
 PS T   VT P
43
The relationships among the partials are Maxwell’s
relations. These relations are enormously useful. Each
partial involves a state variable that can be integrated along
any convenient reversible path between two states to obtain
the difference in the value of a state variable between two
equilibrium states. They can be used to obtain values, or
differences between values, for quantities not easily
measured from more easily measured quantities, such as P,
V or T. They are often used to replace a partial, which
cannot be evaluated, by another partial which can be
determined (see slide 47).
44
The VFT-VUS diagram is a device for
remembering the differential forms of the
potentials. Notice the direction of the arrows. If
you go in a direction opposite to an arrow, the
quantity is negative. The potentials are at the
sides. They are functions of the state variables at
the corresponding corners. The corresponding
conjugate coordinate to the variable is obtained
by following the diagonal arrow.
45
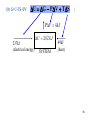
V
F
U
S
T
G
H
P
Consider the Gibbs function, dG will
consist of a dT and a dP. The coefficient
of dT will be -S and the coefficient of dP
will be V.
dG=-SdT+VdP
46
EXAMPLE: Ideal gas undergoes an isothermal reversible process
P0  P Reversible process so Q=TdS
đ
Consider S=S(T,P)
 S 
 S 
 dT    dP
dS  
 T  P
 P T
S 
 dP
 P  T
dT=0 (isothermal) so dS  
đ Q  T S 
 P  T
dP
We cannot evaluate the derivative involving S so we get rid of S by
 S 
 V 
using the Maxwell relation
   

 P 
 T
 V 
đ Q  T  dP
 T  P
nRT
đQ  
dP
P
If P  P0
Ideal gas so
 T 

P
 V 
nR



 T 
PV=nRT
P

P
P
Q  nRT 
P0
dP
P
P
Q  nRT ln 
 P0 
Q<0 and heat flows out of the system.
47
• Clausius-Clapeyron Equation
This is an important relation describing how
the P varies with T for a system consisting of
two phases in equilibrium.
From the VFT-VUS diagram the molar Gibbs
function is given by:
dg = -sdT + vdP
Hence s  

g
T P
and
v
 
g
P T
(reciprocity relations)
{Note that we are concerned with the variables P and T and
these are the natural variables for the Gibb’s Potential.}
48
In a first order phase transition these
variables change as follows:
v
s
phase (i)
phase (f)
T
phase (i)
phase (f)
T
(In higher order phase transformations s
and v are the same.)
49
At the T of the phase transition g is
single valued but the slope is
discontinuous.
slope discontinuity
g
phase (f)
phase (i)
T
50
Two phases can exist in equilibrium at various
combinations of (P, T). On a P, T diagram
there will be a phase boundary (coexistence
curve).
Phase equilibrium line
with g (i) = g (f)
phase (i)
P
b
•
a
phase (f)
•
T
51
We consider a reversible phase change at
constant T and P. As was discussed earlier,
(slide 31) the Gibbs function will remain
constant:
g(i) = g(f)
This is true for all phases in equilibrium, i.e. on
a phase equilibrium line.
Consider the two neighboring points a and b,
separated by dP and dT. The g’s will change as
we go from a to b, but they must remain equal,
so
dg(i) = dg(f)
-s(i) dT + v(i) dP = -s(f) dT + v(f) dP
[Note: P and T are not independent since we are moving
along a phase boundary.]
52
dP
dT
This yields

s( f )  s( i )
v( f )  v( i )
Hence the slope of the phase boundary is
determined by the entropies and volumes of
the two phases .
đQ

dS


S

From
T
T
in which ℓ is the appropriate latent heat, we
therefore have
dP
dT
 

T v (f)  v ( i )

This is the famous Clausius-Clapeyron
equation. It applies to the slope of any
phase boundary line on a PT diagram.
53
Let us consider a sublimation or vaporization curve.
The vapor will be approximated as an ideal gas.
Since v(i) << v(f) we can make the excellent
approximation v(f) - v(i) = v(f).
From the ideal gas law v ( f )  RT
,P
the Clausius-Clapeyron equation now becomes

dP
dT

P2
dP
P1 P
ln
P
RT 2


R

T2
dT
2
T1 T
   
P2
P1
 1
R T2
, giving

1
T1

54
• Example A pressure cooker
At P = 1 atmosphere the BP of water is 373k.
What is the BP at 2 atmospheres? The latent
heat of vaporization is 40.68 kJ/mole.
Using the above equation:
ln 2   R

1
T2

1
373 k

giving T2 = 393.8k = 120.8 0C.
The experimental value is 120.6 0C
(Latent heat has some temperature dependence, but this
can usually be ignored if the range is not very great.) 55
EXAMPLE: Clausius-Clapeyron Equation.
s always
increases
except
Gas
Liquid
Solid
3
dP
s( f )  s( i )
 (f )
dT v  v ( i )


specific volume
usually increases
He below 0.3K


Consider a solid to liquid transition. s ( f )  s (i )  0
dP
(f )
(i )
v v 0
0
If
curve has positive slope
dT
dP
(f )
(i )
v v 0
0
If
curve has negative slope
dT




One of few substances with a negative slope is water
56
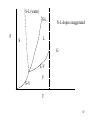
S-L (water)
S-L
P
S-L slopes exaggerated
L
S
G
L-V
V
S-V
T
57
Diamonds and Graphite
These are two phases of C, differing in crystal structure.
At P=1 atm. the most stable phase is graphite, so diamond will
convert spontaneously to graphite, but the process is very slow at
room temperature. The process increases with T, so do not store
your diamonds near the fireplace. Graphite is more stable because
it has a smaller Gibb’s function.
T=298K
g(kJ)
5
1 bar =10 Pa
diamond
2.9 kJ
graphite
0
5
10
15
P (kbar)
Point on phase
equilibrium line
20
58
Above about 15kbar diamond is more stable than graphite at room T.
(Natural diamonds are formed at great depths below the surface of
the Earth, some 100-200 km deep).
Suppose that T is raised to 398K. At what P do these two phases
have the same Gibb’s Function? We start at (298K, 15kbar)
At room temperature (diamond converting to graphite)
3
J
m
s  3.4
v  1.9  10  6
mole  K
mole
From the Clausius-Clapeyron Equation (slope of phase boundary)
J
3.4
(an approximation because entropy
P s
mole

K


3
increases with T)
 T v
6 m
1.9  10
mole
So for a T  100 K
P  1.8kbar
The point on the phase transformation line is then (398K, 16.8kbar).
The first synthesis of diamond from graphite was accomplished at
59
1800 K, 60 kbar
EXAMPLE: Let us use the Clausius-Clapeyron equation to calculate
the decrease in temperature from the triple point to the NMP.
H2 0
P
TP 0.01C 273.16K 612Pa
magnified
5
fusion curve
{NMP 0.00C 273.15K 1.013  10 Pa }
NMP
Apply the Clausius-Clapeyron
equation to fusion curve

TP
T
3
m
v  10 3
kg
dP
dT
 H 2O

T( v  v )

dT 
dP
T( v  v )

kg
 10
m3
3
 ice
3
m
v  1.09  10 3
kg
kg
 916 3
m
1
v

J
  3.34  10
kg
5
60
3
m
273.16K 10 3  1.09  10 3 
kg
dT 
(1.01  105  612)Pa
5 J
3.34  10
kg
dT=-0.0074K
Presence of dissolved air in ice-water mixture further reduces the
temperature by 0.0023K. Hence
dT=-0.0097K
61
EXAMPLE:
Prove that, on a phase diagram, the slope of the sublimation
curve at the triple point is greater than that of the vaporization curve
at the same point.
We consider a substance, such as water, that expands upon
freezing.
v  v ! v  v v  v
H 2O
Fusion curve
From VFT-VUS dH=TdS+VdP
At P=constant
dH=TdS= đ Q
At a phase transformation
Liquid
P

đ Q   dS 
T
(i )
Solid
Vapor
dP s( f )  s

 (f )

(i )
dT v  v
T v(f )  v(i )
  h( f )  h(i )
T


h  h  h  h  h  h
(h  h)  (h  h)  (h  h) 62
 SV   LV   SL
at the triple point
dP 
dP 
dP 



T( v  v )
  T( v  v )
  T( v  v )

 dT  SV
 dT  LV
 dT  SL
Remember that, in this case,
v  v
 dP 
 dP   ( v  v)   dP   ( v  v) 


 
 
 










dT
dT
(
v

v
)
dT
(
v

v
)

 SV 
 LV 
 SL 
 

>1
(-)
(-)
 dP 
 dP 

  

 dT  SV  dT  LV
63