Download Linear Programming

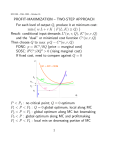
Linear Programming
Piyush Kumar
Welcome to COT 5405
Optimization
For example
Min cT x
subject to Ax  b
x0
This is what is known as a standard linear program.
Linear Programming
Significance
 A lot of problems can be converted to LP
formulation
o Perceptrons (learning), Shortest path, max flow, MST,
matching, …
Accounts for major proportion of all
scientific computations
Helps in finding quick and dirty solutions to
NP-hard optimization problems
 Both optimal (B&B) and approximate (rounding)
Graphing 2-Dimensional LPs
Optimal
Solution
y
Example 1:
4
Maximize
x+y
Subject to: x + 2 y  2
x3
3
Feasible
Region
2
y4
x 0 y 0
1
0
These LP animations were
created by Keely Crowston.
x
0
1
2
3
Graphing 2-Dimensional LPs
y
Example 2:
4
Minimize **
Multiple
Optimal
Solutions!
x-y
Subject to: 1/3 x + y  4
-2 x + 2 y  4
3
2
Feasible
Region
x3
x 0 y 0
1
0
0
1
2
3
x
Graphing 2-Dimensional LPs
y
Example 3:
40
Minimize
x + 1/3 y
Subject to: x + y  20
-2 x + 5 y  150
30
Feasible
Region
20
x5
x 0 y 0
10
x
Optimal
Solution
0
0
10
20
30
40
Do We Notice Anything From
These 3 Examples?
Extreme point
y
y
y
4
4
40
3
3
30
2
2
20
1
1
10
0
0
1
2
3
x
0
0
1
2
3
x
0
x
0
10
20
30
40
A Fundamental Point
y
y
y
4
4
40
3
3
30
2
2
20
1
1
10
0
0
1
2
3
x
0
0
1
2
3
x
0
x
0
10
20
30
If an optimal solution exists, there is
always a corner point optimal solution!
40
Graphing 2-Dimensional LPs
Second
Corner pt.
Example 1:
Optimal
Solution
y
4
Maximize
x+y
Subject to: x + 2 y  2
x3
3
Feasible
Region
2
y4
x 0 y 0
1
Initial
0
Corner pt.
x
0
1
2
3
And We Can Extend this to Higher
Dimensions
Then How Might We Solve an LP?
 The constraints of an LP give rise to a
geometrical shape - we call it a polyhedron.
 If we can determine all the corner points of the
polyhedron, then we can calculate the objective
value at these points and take the best one as our
optimal solution.
 The Simplex Method intelligently moves from corner
to corner until it can prove that it has found the
optimal solution.
But an Integer Program is Different
y
 Feasible region is a set
of discrete points.
 Can’t be assured a
4
3
corner point solution.
 There are no “efficient”
2
ways to solve an IP.
 Solving it as an LP
provides a relaxation
and a bound on the
solution.
1
0
0
1
2
3
x
Linear Programs in higher
dimensions
minimize
subject to
z=
7x1 + x2 + 5x3
x1
- x2
+ 3x3 >= 10
5x1
+ 2x2 -
x1,
x2,
x3
x3 >= 6

0
What happens at (2,1,3)?
What does it tell us about z* = optimal value of z?
LP Upper bounds
Any feasible solution to LP gives an
upper bound on z*
So now we know z* <= 30.
How do we construct a lower bound?
 z* >= 16? [Y/N]?
Lower bounding an LP
7x1+x2+5x3
>= (x1-x2+3x3) + (5x1+2x2-x3)
>= 16
Find suitable multipliers ( >0 ?) to
construct lower bounds.
How do we choose the multipliers?
The Dual
maximize
subject to
z’ =
10y1 + 6y2
y1
+ 5y2 <= 7
-y1
+ 2y2 <= 1
3y1 –
y1,
y2
y2 <= 5

0
What is the dual of a dual?
Every feasible solution of the dual gives a lower bound on z*
The Primal
minimize
z=
subject to
7x1 + x2 + 5x3
x1
- x2
+ 3x3 >= 10
5x1
+ 2x2 -
x1,
x2,
x3
x3 >= 6

0
Every feasible solution of the primal is an upper bound on
the solution to the dual.
Primal – Dual picture
Strong Optimality
Primal = Dual at opt
Z*
0
Dual
Solutions
Primal
Solutions
Duality
A variable in the dual is paired with a
constraint in the primal
Objective function of the dual is determined
by the right hand side of the primal
constraints
The constraint matrix of the dual is the
transpose of the constraint matrix in the
primal.
Linear programming duality
max x1+x2
x1+x2+x3+x4=1
x1+2x3  1
x2+2x4  2
x1  0
x4  0
min y1 + y2 + 2 y3
y2  0
y3  0
y1 + y2  1
y1 + y3 = 1
y1 + 2y2 = 0
y1 + 2y3  0
Duality Properties
Some relationships between the primal and dual problems:
1. If one problem has feasible solutions and a bounded
objective function (and so has an optimal
solution), then so does the other problem, so
both the weak and the strong duality properties
are applicable
2. If the optimal value of the primal is unbounded
then the dual is infeasible.
3. If the optimal value of the dual is unbounded
then the primal is infeasible.
In Matrix terms
Min cT x
subject to Ax  b
x0
Amxn , cnx1 , xnx1
LP Geometry
Forms a n dimensional polyhedron
Is convex : If z1 and z2 are two feasible
solutions then λz1+ (1- λ)z2 is also feasible.
Extreme points can not be written as a
convex combination of two feasible points.
LP Geometry
The normals to the halfspaces defining
the polyhedron are formed by the
coefficents of the constraints.
Rows of A form the normals to the
hyperplanes defining the primal LP
pointing inside the polyhedron.
LP Geometry
Extreme point theorem: If there exists
an optimal solution to an LP Problem,
then there exists one extreme point
where the optimum is achieved.
Local optimum = Global Optimum
Revisiting Shortest Path
v
max dt
ds = 0
du  ds + 2
dv  ds + 6
dw  du + 3
dw  dv + 1
dt  dw + 2
dt  dv + 4
For all nodes x, 0 dx
6
u
t
2
1
s
2
4
w
3
Feasibility = Optimization?
Feasibility Solver can solve LP.
 Write primal and dual constraints.
 Add the constraints that their objective
functions should be equal.
 Solve the resulting feasability problem.
How can one solve feasibility using an
LP solver?
Max-Flow
FLOW CONSERVATION
 fu,v = 0
vV
CAPACITY CONSTRAINTS
fu,v  c(u,v)
SKEW SYMMETRY
fu,v = - fv,u
Max-Flow
objective = ?
us,t:
 fu,v = 0
vV
fu,v  c(u,v)
fu,v + fv,u=0
Max-Flow
us,t:
max vV
 fs,v
 fu,v = 0
vV
fu,v  c(u,v)
fu,v + fv,u=0
LP: Algorithms
Simplex. (Dantzig 1947)
 Developed shortly after WWII in response to logistical problems:
used for 1948 Berlin airlift.
 Practical solution method that moves from one extreme point to a
neighboring extreme point.
 Finite (exponential) complexity, but no polynomial
implementation known.
Courtesy Kevin Wayne
LP: Polynomial Algorithms
Ellipsoid. (Khachian 1979, 1980)
 Solvable in polynomial time: O(n4 L) bit operations.
o n = # variables
o L = # bits in input
 Theoretical tour de force.
 Not remotely practical.
Karmarkar's algorithm. (Karmarkar 1984)
 O(n3.5 L).
 Polynomial and reasonably efficient
implementations possible.
Interior point algorithms.
 O(n3 L).
 Competitive with simplex!
o Dominates on simplex for large problems.
 Extends to even more general problems.
Ellipsoid Method
Courtesy S. Boyd
Barrier Algorithms
Simplex solution path
Barrier central path
o Predictor
o Corrector
Optimum
Interior Point Methods
Back to LP Basics
Standard form of LP
Min cT x
subject to Ax  b
x0
Amxn , cnx1 , xnx1
Standard form of the Dual
Max bT y
subject to AT y  c
y0
Amxn , cnx1 , xnx1
Weak Duality
b y ( Ax ) y  x A y  x c  c x
T
T
T
T
T
T
We will not prove strong duality in this class
but assume it.
Complementary solutions
For any primal feasible (but suboptimal)
x, its complementary solution y is dual
infeasible, with cx=yb
For any primal optimal x*, its
complementary solution y* is dual
optimal, with cx*=y*b=z*
Duality Gap = cx-yb
Complementary slackness
x*, y* are feasible, then they are optimal
for (P) and (D) iff
 For I = 1..m if yi* > 0
o Then aix* = bi
 For J = 1..n if xj* > 0
o Then y*Aj = ci
ai are rows of A and Aj are the columns of A
Complementary slackness
x*, y* are simultaneously optimal for (P)
and (D) iff
 y*(Ax* - b) = 0
 (y*A – c)x* = 0
Summary: If a variable is positive, its dual constraint is tight
Or if a constraint is loose its dual variable is zero.
Complementary Slackness
Proof?
y*(Ax* - b) - (y*A – c)x*
= y*Ax* - y*b - y*Ax* + cx*
= cx* - y*b
=0
( But all terms are non-negative )
Hence all must be zero!
Primal-Dual Algorithms
Find a feasible solution for both P and
D.
Try to satisfy the complementary
slackness conditions.
Algorithm Design Techniques
LP Relaxation
 Rounding
o Round the fractional solution obtained by
solving LP-relaxation.
o Runs fast 
 Primal Dual Schema
o (iteratively constructs primal n dual solutions)
y
objective
LP optimum
feasible solutions
x
Linear Program
y
objective
optimum of
LP relaxation
IP optimum
feasible
solutions =
rounding down optimum
of LP relaxation
x
Integer Program
Linear Relaxations
What happens if the optimal of a LPRelaxation is Integral?
There are a class of IPs for which this is
guaranteed to happen
 Transportation problems
 MaxFlow problems
 In general (Unimodularity) … Exact Relaxation
Lower Bounds
Assume minimization problem
Any relaxation of the original IP has a _____________
optimal objective function value than the optimal objective
function value of the original IP
z*relaxation
z*
z*relaxation is called a __________________ on z*
Difference between these two values is called the relaxation
gap
Upper Bounds
Any feasible solution to the original IP has a
_____________ objective function value than the optimal
objective function value of the original IP
zfeasible
z*
zfeasible is called an __________________ on z*
Heuristic techniques can be used to find “good” feasible
solutions
 Efficient, may be beneficial if optimality can be
sacrificed
 Usually application- or problem-specific
Vertex Cover
Introduction to LP Rounding
A simple 2-approximation using LP
Better than 2-factor approx?