Download Example 5

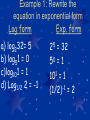
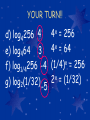
Math 3
Keeper 27
Logarithms
Essential Question – How is
a log function related to an
exponential function?
You use log functions to solve
exponential problems; they
are inverses of each other.
When will I use this?
•
•
•
•
Human memory
Intensity of sound (decibels)
Finance
Richter scale
Evaluating Log Expressions
• We know 22 = 4 and 23 = 8
• But for what value of y does 2y = 6?
• Because 22<6<23 you would expect
the answer to be between 2 & 3.
• To answer this question exactly,
mathematicians defined logarithms.
• Logarithms are the INVERSE of
exponential functions.
Definition of Logarithm to base b
Let b & x be positive numbers, b ≠ 1.
logby = x iff bx = y
• This expression is read “log base b of y”
• The definition tell you that the equations
logby = x and bx = y are equivalent.
Example 1: Rewrite the
equation in exponential form
Log form
Exp. form
a) log232= 5
b) log51 = 0
c)log101 = 1
d) Log1/2 2 = -1
5
2
= 32
0
5 =1
101 = 1
(1/2)-1 = 2
YOUR TURN!!
Log form
e) log39= 2
f) log81 = 0
g)log5(/25)=-2
Exp. form
32 = 9
0
8 =1
-2
5 = 1/25
Rewriting forms:
To evaluate log3 9 = x ask yourself…
“3 to what power is 9?”
3x = 9 → 32 = 9 so……
log39 = 2
Example 2: Evaluate the
expression without a calculator
a)log381 4
x
3
= 81
b) log50.04 -2
x
5
= 0.04
c) log5125 3
5x = 125
YOUR TURN!!
x
4
= 256
d) log4256 4
x
4 = 64
e) log464 3
x = 256
(1/4)
f) log1/4256 -4
x
2 = (1/32)
g) log2(1/32)
-5
You should learn the following
general forms!!!
0
b
• Log b 1 = 0 because
=1
1
• Log b b = 1 because b = b
• Log b bx = x because bx = bx
Natural logarithms
log e x = ln x
• The natural log is the inverse of the
natural base, e.
• ln means log base e
Common logarithms
log 10 x = log x
• Understood base 10 if nothing is there.
Common logs and natural logs with
a calculator
log10 button
ln button
Example 3: Use a calculator to evaluate
the expression. Round answer to 3 decimal
places.
a) log 5
0.6989= 0.700
b) ln 0.1
-2.303
c) log 7
0.845
d) ln 0.25
-1.386
INVERSE PROPERTIES
g(x) = log b x is the inverse of the
exponential function f(x) = bx
f(g(x)) = blogbx = x
g(f(x)) = logbbx = x
*Exponential and log functions are
inverses and “undo” each other
Example 4: Using inverses→
Simplify the expression.
a) 10log2 = 2
x
b) log39 = log3(32)x = log332x= 2x
c) 10logx = x
3)x = log 53x = 3x
x
log
(5
d) log5125 = 5
5
Finding Inverses
Find the inverse of
y = log3x
• By definition of logarithm, the inverse is
y=3x
OR write it in exponential form and
switch the x & y!
3y = x → 3 x = y
Example 5: Find the inverse of...
a) y = ln (x +1)
X = ln (y + 1)
x = loge(y + 1)
ex = y + 1
ex – 1 = y
y = ex – 1
Switch the x & y
Write in log form
Write in exp form
Solve for y
Final Answer
Example 5: Find the inverse of...
b) y = log8x
y
8 =x
x
8 =y
x
y=8
Switch x & y
Solve for y
Final Answer
Example 5: Find the inverse of...
c) y = ln (x - 3)
y = ex + 3
d) y = log2/5x
y = (2/5)
e) Y = ln (x–10)
y = ex + 10
x