Download Homework 28 Answers Conditions for #1

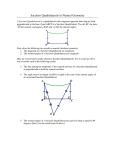
Homework 28 Answers
Conditions for #1-6: Assume the axioms, definitions, and theorems of neutral geometry. Let l
and m be two distinct lines, and P and Q two distinct points on m that are on the same side of l.
Drop perpendiculars from P and Q to the line l, and call the feet P' and Q', respectively.
1. Suppose that P' = Q' (RAA). Then since P and Q are distinct
points and do not lie on l, it follows that PQP' is a triangle.
P R
Q
m
Let R be a point in the interior of PQ. Choose points A and B
on l such that A lies on the same side of P′R as P and B lies
on the same of P′R as Q. Note that ∠AP'P, ∠AP'Q, ∠BP'P,
l
and ∠BP'Q are all right angles. Furthermore, Q is in the
A
P'=Q'
B
interior of ∠PP'B (Converse of Crossbar Thm). So µ(∠PP'B)
= µ(∠PP'Q) + µ(∠QP'B) (Protractor Thm). But µ(∠AP'P) +
µ(∠PP'B) = 180 ⇒ µ(∠AP'P) + µ(∠PP'Q) + µ(∠QP'B) = 180 ⇒ µ(∠PP'Q) = 0, a
contradiction. So P' ≠ Q'.
2. We've already shown that P' ≠ Q'. Suppose that PP′ ∩ QQ! ≠ ∅. Let
E be the point of intersection. Then E doesn't lie on l, otherwise P' =
Q'. So EP'Q' is a triangle. Note that ∠EP'Q' = ∠PP'Q', a right
angle, and ∠EQ'P' = ∠QQ'P', a right angle. We know that
σ(EP'Q') ≤ 180 ⇒ ∠P'EQ' = 0, a contradiction. So PP′ ∩ QQ! =
∅.
m
Q
P
l
Q'
E
P'
3. We know that P, Q, P', and Q' are distinct points by #1. By #2,
PP′ and QQ′ do not intersect. Also, because P and Q are on the
Q
m P
same side of l, we know that PQ and P′Q′ do not intersect (Plane
Separation). What about adjacent sides, such as PP′ and PQ?
Because these segments already intersect at P, if they intersect at
l
Q'
another point, then P, Q and P' would be on the same line, which
P'
would make m ⊥ l because P' is the foot of the perpendicular
from P to l. Then QP'Q' would be a triangle with two right angles, a contradiction. So these
two segments cannot intersect at a point other than P. Similarly, all other adjacent sides can
intersect only at endpoints. So PQQ'P' is a quadrilateral.
4. If If d(P, l) = d(Q, l), then PP'Q'Q is a Saccheri quadrilateral, since base angles are right
angles and the two sides are of equal length. If d(P, l) ≠ d(Q, l), then it is a trapezoid, because
the two sides are parallel by the Corresponding Angles Thm.
5. Since d(P, l) = d(Q, l), PP'Q'Q is a Saccheri quadrilateral, and one of the properties of a
Saccheri quadrilateral is that opposite sides are parallel. So l || m.
6. If P and Q are on opposite sides of l, then PQ intersects l, which implies that m intersects l, so
l and m are not parallel.
7. They must be parallel by the Alternate Angles Thm.
9. Let P and Q be two points on m such that d(P, l) = d(Q, l). Drop perpendiculars from P and Q
to l, and call the feet A and B respectively. By #4, ABQP is a
Q
N
Saccheri quadrilateral. Let M be the midpoint of AB and N be the
m P
midpoint of PQ. Then by the properties of Saccheri quadrilaterals,
MN is perpendicular to both l and m. So l and m admit a common
l
Q'
perpendicular.
M
P'
10. Let l and m admit a common perpendicular n. Let n intersect l at P and m at Q. Suppose there
exists n' such that n' ⊥ l and n' ⊥ m. Let n' intersect l at P' and m
at Q'. Suppose that P ≠ Q (RAA). We can think of n as the
m
Q'
Q
perpendicular dropped from Q to l and n' as the perpendicular
dropped from Q' to l. Then by #3, PP'Q'Q is a quadrilateral.
P'
l
P
Furthermore, all four angles of PP'Q'Q are right angles, which
n
means it is a rectangle. But this is a contradiction in hyperbolic
n'
geometry. Therefore, P = P'. But then Q = Q' by the same proof
used in #1. So n = n'.