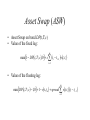Download Lecture 1

Advanced methods of insurance
Lecture 1
Example of insurance product I
• Assume a product that pays
– A sum L if the owner dies by time T
– A payoff max(SP(T)/SP(0), 1 + k)
• Pricing factors
–
–
–
–
Risk free discount factor v(t,T)
Survival function S(t,T)
Level of the underlying asset SP(t)
Volatility of SP(t)
Example of insurance product II
• Assume a product that pays
– A sum L if the owner dies by time T
– A payoff max(min(Si(T)/S(0)), 1 + k)
• Pricing factors
–
–
–
–
–
Risk free discount factor v(t,T)
Survival function S(t,T)
Level of the underlying asset SPi (t)
Volatility of SPi(t)
Correlation of the asset SPi(t).
How do you pay for the product?
• You may pay for the product in a unique
payment.
• Alternatively, you may pay on a running
basis, with several payments until maturity,
if you survive to maurity.
• In case one dies, the payments would stop
and a fraction of the amount paid is given to
the heirs.
Financial and insurance products
• Financial products allow to trnasfer consumption
from the current to future periods.
• Insurance products introduce actuarial risks such
as the risk of death for an individual underwriting
a life insurance policy or the risk of catastrophic
loss for a product that is indexed non-life
insurance risks.
• In this course we review the main instruments that
could be used to transfer consumption and risk
from the present to the future.
Financial and insurance products
• Fixed income. Bonds. Pay-off is defined
independently from the project funded.
• Variable income. Equity. Pay-off is a function of
the proceedings from the project.
• Derivatives. Contingent claims. Products whose
value is defined as a function of other risky assets
• Managed funds: funds aggregated and managed on
behalf of customers
• Insurance policies: life, death and mixed.
Financial structures: ingredients
• Schedule: {t0, t1, …,tn}
– Calendar conventions
– Day-count conventions
• Coupon plan: {c0, c1, …,cn}
– Deterministic
– Indexed (interest rates, inflation, equity, credit,
commodities, longevity, …)
• Repayment plan {k0, k1, …,kn}
– Deterministic
– Stochastic (callable, putable, exchangeable,
convertible)
Working in finance or insurance
• Structurer: design products, identifying possible
customers and including possible clauses.
• Pricer: evaluated the product, “marking-tomarket” the elementary elements of the product
• Risk manager: evaluate the exposures to risk
factors, and both expected and unexpected risks,
as well as their dependence.
• NB. All these operations are based on the
decomposition of the product in elementary units.
Arbitrage principle
• We say that there exists an arbitrage
opportunity (free lunch) if in the economy it
is possible to build a position that has
negative or zero value today and positive
value at a future date (positive meaning
non-negative in one state and positive in at
least one)
Replicating portfolio
• A replicating portfolio or a replicating strategy
of a financial product is a set of postions whose
value at some future date is equal to that of the
financial product with probability one.
• If it is possible to build a replicating portfolio or
strategy of a financial product for a price
different from that of the product, one could
exploit infinite arbitrage profits selling what is
more expensive and buying what is cheaper.
Replicating portfolio for
valuation and hedging
• Saying that no arbitrage profits are possible
means to require that the value of each
financial product is equal to the value of its
replicating portfolio and strategy (pricing)
• Buying the financial product and selling the
replicating portfolio enables to immunize
the position (hedging).
Zero-coupon-bond
• Define P(t,tk,xk) the value at time t of a zero-coupon bond
(ZCB). It is a security that does not pay coupons before
maturity and that gives right to receive a quantity xk at a
futurre date tk
• Define v(t,tk) the discount funtion, that is the value at time
t of a unit of cash available in tk
• Assuming infinite divisibility of each bond, down to the
bond paying one unit at maturity, we obtain that
P(t,tk,xk) = xk v(t,tk)
Coupon bond evaluation
Let us define P(t,T;c) the price of a bond paying coupon c on a
schedule {t1, t2, …,tm=T}, with trepayment of capital in one sum at
maturity T. The cash flows of this bond can be replicated by a basket
of ZCB with nominal value equal to c corresponding to maturities ti
for i = 1, 2, …, m – 1 and a ZCB with a nominal value 1 + c iat
maturity T. The arbitrage operation consisting in the purchase/sale of
coupons of principal is called coupon stripping.
m
P(t , T ; c)   cv(t , t k )  v(t , t m )
k 1
Bond prices and discount factors
• Based on zero-coupon bond prices and the prices
of coupon bonds observed on the market it is
possible to retrieve the discount function.
• The technique to retrieve the discount factor is
based on the no-arbitrage principle and is called
bootstrapping
• The discount function establishes a financial
equivalence relationship between a unit amount
of cash available at a future date tk and an amount
v(t,tk) available in t.
• Notice that the equivalence holds for each issuer.
Bootstrapping procedure
Assume that at time t the market is structured on m periods
with maturities tk = t + k, k=1....m, and assume to observe
zero-coupon-bond P(t,tk) prices or coupon bond prices
P(t,tk;ck). The bootstrapping procedure enables to recover
discount factors of each maturity from the previous ones.
k 1
vt , t k  
Pt , t k ; ck   ck  vt , ti 
i 1
1  ck
The term structure of interest rates
The term structure is a way to represent the discount function.
It may be represented in terms of discrete compounding
1
v(t , t k ) 
t k  t 
1  i(t , tk )
i (t , t k )  v(t , t k )
1 / t k t 
1
The term structure of interest rates
The term structure is a way to represent the discount function.
It may be represented in terms of continuous compounding
v(t , t k )  exp  i t , t k t k  t 
ln v(t , t k )
i (t , t k )  
tk  t
The term structure of interest rates
The term structure is a way to represent the discount function.
It may be represented in terms of discrete compounding
1
v(t , t k ) 
1  t k  t i (t , t k )
1
i (t , t k ) 
tk  t
 1

 1

 v(t , t k ) 
Term (forward) contracts
• A forward contract is the exchange of an amount
v(t,,T) fixed at time t and paid at time  ≥ t in
exchange for one unit of cash available at T.
• A spot contract is a specific instance in which
 = t, so that v(t,,T) = v(t,T).
• v(t,,T) is defined as the (forward price)
established in t of an investment starting at  ≥ t
and giving back a unit of cash in T.
Spot and forward prices
•
•
•
Consider the following strategies
1. Buy a nominal amount v(t,,T) availlable at  on the
spot market and buy a forward contract for settlement
at time , giving a unit of cash available on T
2. Issue debt on the spot market for repayment of a unit
of cash at time T.
It is easy to see that this strategy yields a zero
pay-off at time both at time  and at time T.
If the value of the strategy at time t is different
from zero, there exists an arbitrage opportunity
for one of the two parties.
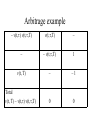
Arbitrage example
– v(t,) v(t,,T)
v(t,,T)
–
–
– v(t,,T)
1
v(t, T)
–
–1
Total
v(t, T) – v(t,) v(t,,T)
0
0
Spot and forward prices
• Spot and forward prices are then linked by a
relationship that rules out the arbitrage opportunity
described above
v(t,T)=v(t,) v(t,,T)
• All the information on forward contracts is then
completely contained in the spot discount factor
curve.
• Caveat. This is textbook paradigm that is under
question today. Can you guess why?
The forward term structure
Forward term structure is a way of representing the forward
discount function.
It may be represented with discrete compounding.
f (t , , T )  v(t , , T )
 v (t , ) 


 v (t , T ) 
1 / T  
1
1 / T  
1
The forward term structure
Forward term structure is a way of representing the forward
discount function.
It may be represented with continuous compounding.
ln v(t , , T )
f (t , , T )  
T 
ln v(t , )  ln v(t , T )

T 
i (t , T )(T  t )  i (t , )(  t )

T 
The forward term structure
Forward term structure is a way of representing the forward
discount function.
It may be represented with linear compounding.
1
f (t , , T ) 
T 
1

T 


1
 v(t , , T )  1


 v(t , ) 
 v(t , T )  1


Indexed (floating) coupons
• An indexed coupon is determined based on a
reference index, typically an interest rates,
observed at time , called the reset date.
• The typical case (known as natural time lag) is a
coupon with
– reference period from  to T
– reset date  and payment date T
– reference interest rate for determination of the coupon
i( ,T) (T –  ) = 1/v ( ,T) – 1
Replicating portfolio
• What is the replicating portfolio of an floating
coupon, indexed to a linear compounded interest
rate for one unit of nominal?
• Notice that at the reset date  the value of the
coupon, determined at time  and paid at time T,
will be given by
v ( ,T) i( ,T) (T –  ) = 1 – v ( ,T)
• The replicating portfolio is then given by
– A long position (investment) of one unit of nominal
available at time 
– A short position (financing) for one unit of nominal
available at time T
Cash flows of a floating coupon
• Notice that a floating coupon on a nominal
amount C corresponds to a position of debt
(leverage)
C
t

T
C
No arbitrage price:
indexed coupons
• The replicating portfolio enables to evaluate the coupon at time t
as:
indexed coupons = v(t,) – v(t,T)
At time  we know that the value of the position is:
1 – v(,T) = v(,T) [1/ v(,T) – 1]
= v(,T) i(,T)(T – )
= discount factor X indexed coupon
• At time t the coupon value can be written
v(t,) – v(t,T) = v(t,T)[v(t,) / v(t,T) – 1]
= v(t,T) f(t,,T)(T – )
= discount factor X forward rate
Indexed coupons: some caveat
• It is wrong to state that expected future coupons
are represented by forward rates, or that forward
rates are unbiased forecasts of future forward rates
• The evaluation of expected coupons by forward
rates is NOT linked to any future scenario of
interest rates, but only to the current interest rate
curve.
• The forward term structure changes with the spot
term structure, and so both expected coupons and
the discount factor change at the same time (in
opposite directions)
Indexed cash flows
• Let us consider the time schedule
t,t1,t2,…tm
where ti, i = 1,2,…,m – 1 are coupon reset times,
and each of them is paid at ti+1.
t is the valuation date.
• It is easy to verify that the value the series of
flows corresponds to
– A long position (investment) for one unit of nominal at
the reset date of the first coupon (t1)
– A short position (financing) for one unit of nominal at
the payment date of the last coupon (tm)
Floater
• A floater is a bond characterized by a schedule
t,t1,t2,…tm
– at t1 the current coupon c is paid (value cv(t,t1))
– ti, i = 1,2,…,m – 1 are the reset dates of the floating coupons
are paid at time ti+1 (value v(t,t1) – v(t,tm))
– principal is repaid in one sum tm.
• Value of coupons: cv(t,t1) + v(t,t1) – v(t,tm)
• Value of principal: v(t,tm)
• Value of the bond
Value of bond = Value of Coupons + Value of Principal
= [cv(t,t1) + v(t,t1) – v(t,tm)] + v(t,tm)
=(1 + c) v(t,t1)
• A floater is financially equivalent to a short term note.
Forward rate agreement (FRA)
• A FRA is the exchange, decided in t, between a floating
coupon and a fixed rate coupon k, for an investment period
from  to T.
• Assuming that coupons are determined at time , and set
equal to interest rate i(,T), and paid, at time T,
FRA(t) = v(t,) – v(t,T) – v(t,T)k
= v(t,T) [v(t,)/ v(t,T) –1 – k]
= v(t,T) [f(t,,T) – k]
• At origination we have FRA(0) = 0, giving k = f(t,,T)
• Notice that market practice is that payment occurs at time 
(in arrears) instead of T (in advance)
Natural lag
• In this analysis we have assumed (natural lag)
– Coupon reset at the beginning of the coupon period
– Payment of the coupon at the end of the period
– Indexation rate is referred to a tenor of the same length
as the coupon period (example, semiannual coupon
indexed to six-month rate)
• A more general representation
Expected coupon = forward rate
+ convexity adjustment + timing adjustment
• It may be proved that only in the “ natural lag” case
convexity adjustment + timing adjustment = 0
Esercise
Reverse floater
• A reverse floater is characterized by a time
schedule
t,t1,t2,…tj, …tm
– From a reset date tj coupons are determined on the
formula
rMax –  i(ti,ti+1)
where  is a leverage parameter.
– Principal is repaid in a single sum at maturity
Swap contracts
• The standard tool for transferring risk is the swap
contract: two parties exchange cash flows in a
contract
• Each one of the two flows is called leg
• Examples of swap
– Fixed-floating plus spread (plain vanilla swap)
– Cash-flows in different currencies (currency swap)
– Floating cash flows indexed to yields of different
countries (quanto swap)
– Asset swap, total return swap, credit default swap…
Swap: parameters to be determined
• The value of a swap contract can be expressed as:
– Net-present-value (NPV); the difference between the
present value of flows
– Fixed rate coupon (swap rate): the value of fixed rate
payment such that the fixed leg be equal to the floating
leg
– Spread: the value of a periodic fixed payment that
added to to a flow of floating payments equals the fixed
leg of the contract.
Plain vanilla swap (fixed-floating)
• In a fixed-floating swap
– the long party pays a flow of
fixed sums equal to a
percentage c, defined on a year
basis
– the short party pays a flow of
floating payments indexed to a
market rate
• Value of fixed leg:
m
c  ti  ti 1 vt , ti 
i 1
• Value of floating leg:
m
1  vt , t m    vt , ti ti  ti 1  f t , ti 1 , ti 
i 1
Swap rate
• In a fixed-floating swap at origin
Value fixed leg = Value floating leg
m
swap rate  ti  ti 1 vt , ti   1  vt , t m 
i 1
swap rate 
1  vt , t m 
m
 t
i 1
i
 ti 1 vt , ti 
Swap rate
• Representing a floating cash flow in terms of forward
rates, a swap rate can be seen as a weghted average of
forward rates
m
m
i 1
i 1
swap rate  ti  ti 1 vt , ti    vt , ti ti  ti 1  f t , ti 1 , ti 
m
swap rate 
 vt , t t
i
i 1
m
 t
i 1
i
i
 ti 1  f t , ti 1 , ti 
 ti 1 vt , ti 
Swap rate
• If we assume ot add the repayment of principal to both
legs we have that swap rate is the so called par yield
(i.e. the coupon rate of a fixed coupon bond trading at
par)
m
swap rate  ti  ti 1 vt , ti   1  vt , t m 
i 1
m
swap rate  ti  ti 1 vt , ti   vt , t m   1
i 1
Bootstrapping procedure
Assume that at time t the market is structured on m periods
with maturities tk = t + k, k=1....m, and assume to observe
swap rates on such maturities. The bootstrapping procedure
enables to recover discount factors of each maturity from the
previous ones.
k 1
vt , t k  
1  swap rate t,tk  vt , ti 
i 1
1  swap rate t,tk 
Forward swap rate
• In a forward start swap the exchange of flows
determined at t begins at tj.
Value fixed leg = Value floating leg
forward swap rate  ti  ti 1 vt , ti   vt , t j   vt , t m 
m
i j
forward swap rate 
vt , t j   vt , t m 
m
 t
i  j1
i
 ti 1 vt , ti 
Swap rate: summary
The swap rate can be defined as:
1. A fixed rate payment, on a running basis,
financially equivalent to a flow of indexed
payments
2. A weighted average of forward rates with
weights given by the discount factors
3. The internal rate of return, or the coupon, of a
fixed rate bond quoting at par (par yield curve)
Asset Swap (ASW)
• L’asset swap is a package of
– A bond
– A swap contract
• The two parties pay
– The cash flows of a bond and the difference between
par and the market value of the bond, if positive
– A spread over the floating rate and the difference
between the market value of the bond and par, if
positive
Asset Swap (ASW)
• Asset Swap on bond DP(t,T;c)
• Value of the fixed leg:
m
max 1  DP t , T ; c ,0  c ti  ti 1 vt , ti 
i 1
• Value of the floating leg:
m
max DP t , T ; c   1,0  1  vt , t m   spread  vt , ti ti  ti 1 
i 1
Asset Swap (ASW) Spread
• The spread is obtained equating the value of
the two legs
spread  c  tasso swap 
1  DP t , T ; c 
m
 t
i 1
i
 ti 1 vt , ti 
Structuring choices
• Natural lag:
– Reference period of payment is equal to the tenor of the
reference rate
– Reset date at the beginning of the period (in advance)
• “In arrears”:
– Coupons reset and paid at the same date
• CBM/CMS: coupon indexed to long term interest
rates and swap rates.