Download Solving Systems By Graphing

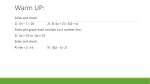
Solving Systems By Graphing
Slope-Intercept Form
y = mx + b
m = slope
b = y-intercept
• Slope-Intercept form
for the equation of a
line
• Slope = rise
run
• y-intercept is the point
where the line
crosses the y-axis
Graph:
1st: graph the y-intercept (the b)
y=½x+3
2nd: follow the slope (rise over run)
3rd: connect the dots
We’re graphing lines, so don’t
forget to draw a line!
Standard Form
Ax + By = C
• Standard form for the
equation of a line
Ax = C
• Finds the x-intercept
+By = C
• Finds the y-intercept
Definition of an Intercept
• An intercept is the point where a line crosses
either of the axes.
• When the line crosses the y-axis, it is called the
y-intercept
• When the line crosses the x-axis, it is called the
x-intercept
• The coordinates for a y-intercept comes in the
form (0,y)
• The coordinates for an x-intercept comes in the
form (x, 0)
Graphing Standard Form
Graph: 3x – 4y = 24
3x – 4(0) = 24
3x = 24
3
3
x=8
• 1st find the x-int
• Set y = 0
• Solve for x
Graphing Standard Form
3(0) – 4y = 24
-4y = 24
-4 -4
• Now solve for y
• Set x = 0
y = -6
• Now graph the
intercepts with those
values that we found
Graph:
1st: graph the x-intercept: 8
3x – 4y = 24
2nd: graph the y-intercept: -6
3rd: connect the dots
We’re graphing lines, so don’t
forget to draw a line!
Solving Systems of Equations
• A system of equations is 2 or more equations using the
same 2 or more variables
• Can be solved 3 ways
– By graphing
– By substitution
– By elimination
• We will focus on the graphing part now
• The solution to a system is the set of all points both lines
have in common
Solving Systems of Equations
• There are 3 possibilities when solving a
system of equations.
– There can be 1 solution (intersecting lines)
– There can be no solution (parallel lines)
– There can be infinitely many solutions (same
line)
• Let’s see an example of each
Solve:
1st: graph the 1st equation
y=½x+3
2nd: graph the 2nd equation
y = 4x - 4
3rd: the solution is the point of
intersection
Our Solution is (2,4)
Solve:
1st: graph the 1st equation
y = 2x + 3
2nd: graph the 2nd equation
y = 2x – 1
3rd: These are parallel lines
There is no solution
Solve:
1st: graph the 1st equation
y=¾x–2
2nd: graph the 2nd equation
y=¾x–2
3rd: These are the same line
There are infinitely many solutions