* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download HEAT OF VAPORIZATION (H v )
Vapor-compression refrigeration wikipedia , lookup
Intercooler wikipedia , lookup
Solar water heating wikipedia , lookup
R-value (insulation) wikipedia , lookup
Solar air conditioning wikipedia , lookup
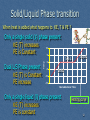
Underfloor heating wikipedia , lookup
Heat exchanger wikipedia , lookup
Heat equation wikipedia , lookup
Copper in heat exchangers wikipedia , lookup
Cogeneration wikipedia , lookup
Mr. Shields Regents Chemistry U07 L03 1 Phase Changes Let’s review what we’ve learned previously about PHASE CHANGES. First … What is a phase change? A change from one state of matter to another. What does endothermic and exothermic mean? Absorbs heat / Releases heat 2 Phase Change Overview What are the names of the phase changes we’ve studied? Gas e Energy Absorbed Endothermic a Exothermic c Energy Released Liquid f d b Solid ENDOTHERMIC Phase changes EXOTHERMIC Phase Chages a. d. Deposition b. Fusion e. Condensation c. f. Solidification Sublimation Vaporization 3 Phase Changes What actually happens to E as matter moves from Solid Liquid Gas: Energy is absorbed (endo) Temp increases KE increases molecules move further apart PE increases (Why?) Remember … PE is a function of the position of two bodies relative to one another So … PE inc as molecular separation increases 4 Heating Curve What happens when we keep adding energy to a solid ? Solid becomes a liquid then the liquid becomes a gas The answer is NO! 15 10 Temp As this energy is added KE inc and so does Temp. but does temp Uniformly inc. over time? 20 5 0 -5 -10 -15 -20 Time 5 Heating Curve So what does happen if the temperature does not Uniformly increase? What happens is described by what is called the HEATING CURVE 6 Heating Curve If we heat a solid it’s temperature increases Steadily until we finally reach the temperature at which the solid begins to melt It begins to go thru a phase change solid Liquid This phase change is called fusion 7 Solid/Liquid Phase Transition As the solid begins to melt something Unusual Happens. As we continue to add heat to the solid the temperature stops rising as the solid continues to melt. 10 Temp 5 But why does this happen? Melting Solid 0 -5 -10 Solid -15 Heat added over Time 8 Solid/Liquid Phase Transition Solids exist in a rigid, closely packed, highly structured pattern Liquids however have no such rigid structure. As we reach the solids m.p. there is just enough energy to begin overcoming the intermolecular forces between molecules holding them together in the solid state... Molecules begin to separate 9 Heat of Fusion Added additional heat energy goes into Separating more and more molecules As molecules move from solid to liquid the PE Increases but since the temperature doesn’t rise The KE remains constant. The energy necessary to melt 1 GRAM of a solid is called the … HEAT OF FUSION (Hf) It is unique for every substance. For water, the heat of fusion = 334 Joules/gram 10 Solid/Liquid Phase transition Remember… heat ALWAYS flows from hot to cold H C Until the last piece of solid melts the temperature the Solid/liquid mixture remains constant Any excess heat in the liquid immediately flows back into the colder solid Once there’s no solid left all additional heat added begins to increase the temperature of the liquid. 11 Solid/Liquid Phase transition When heat is added what happens to KE, T & PE ? Dual L/S Phase present KE (T) is Constant PE increase Temp Only a single solid (s) phase present KE (T) increases 10 PE is Constant 5 S&L Liquid 0 -5 Solid -10 -15 Heat added over Time Only a single liquid (l) phase present KE (T) increases PE is constant Heating curve 12 Liquid/Vapor Phase transition B.P Once VP = Patm the liquid Boils. Temp Any additional heat added To the liquid inc. Temp. and 100 Vapor Pressure. 5 S&L Liquid 0 -5 Solid -10 -15 Heat added over Time As in the transition from solid To liquid, 2 phases are now present & the Temp. of the boiling water remains constant 13 Heat of Vaporization Molecules in the liquid phase form a close but loosely organized structure 125 105 Gas 85 Temp Molecules in the gas Phase have no structure And are widely separated. L&G 65 45 25 5 -15 S&L Solid Liquid Heat added over Time To separate these molecules this much takes lots of energy. This energy is called the HEAT OF VAPORIZATION (Hv) 14 Heat of Vaporization For water, Hv = 2,260 Joules/g As long as the liquid is boiling T and KE will be Constant PE will Increase as molecules Move further apart In the gas phase M.P Note Hv > Hf The Heating Curve B.P. Liquid & gas Solid & liquid 15 Summary (b.p.) Hv = 2,260 J/g T const. / KE const. /PE inc ( 2 phases ) T inc. / KE inc / PE Const. ( 1 phase ) Hf = 334 J/g (m.p.) 16 A Review: Specific Heat Recall from our earlier discussions that … The SPECIFIC HEAT of a substance is the amount of heat required to raise the temperature of 1 g of the material by 1 degree centigrade. Each substance has it’s own unique specific heat… The lower the specific heat the better the conductor And …. q = Cp x m x (Tf – Ti) 17 Specific Heat One of the variables in Specific heat calculations Involves Temperature Change. The Heating Curve Phase V What phases of the The heating curve Involve changes in T? Phase III Phase IV Phase 1 Phase II Phase 1, 3, 5 18 Specific Heat It’s in these phases that specific heat calculations are used to determine how much heat us needed to raise the temperature of the sample The Heating Curve Phase V Phase III Phase IV But how do we find the heat necessary to to fully melt or vaporize a sample of matter In regions where T does Not change (phase II & IV) Phase 1 Phase II 19 Melting/Vaporization Calculations It’s even easier than specific heat calculations since Temperature is not a variable. In phase II: Q= m x Hf m=total mass Hf=heat of fusion The Heating Curve Phase V Phase III Phase IV Phase 1 Phase II In phase IV: Q=m x Hv 20 Melting/Vaporization Calculations Problem 1: How much heat is necessary to melt 100g of ice? Problem 2: How much heat is necessary to vaporize this water? Q = m x Hf Q = 100g x 334 J/g Q = 33,400 J The Heating Curve Phase V Phase III Phase IV Phase 1 Phase II Q = m x Hv Q = 100g x 2,260 J/g Q = 226,000 J 21 Melting/Vaporization Calculations Note that these calculations are true for all sorts of matter, not just water. For example here are some Hv as a function of the intermolecular force: H2O NH3 H2S F2 Hydrogen Bonding Hydrogen Bonding Dipole-Dipole London Dispersion 2260 J/g 1276 J/g 553 J/g 155 J/g 22 Melting/Vaporization Calculations Problem: What is the heat of vaporization of a liquid if it takes 6500 J to totally vaporize 8g? Q = m x Hv 6500 J = 8g x Hv Hv = 6500 / 8 = 812.5 J/g 23 Heat of Fusion and Vaporization from heating graphs If heat is added at a constant rate over time to a specific mass we can determine both Hf and Hv by noting both the initial onset of melting or vaporization and the completion point. 24 Heat of Fusion and Vaporization from heating graphs For example in this graph the onset of vaporization occurs after 875 Joules have been added and is complete after 3100 J have been added. Therefore It took 3100-875 KJ to Vaporize this sample. If the mass of the Sample is 300g then the Hv = 2225KJ/300g =7.417 KJ/g The same can be done To calculate the Hf 875 KJ 3,100 KJ 25 Heat of Fusion and Vaporization from heating graphs If we add heat to a sample at a fixed rate, say 422.4 J/min, we Can then calculate both Hf and Hv if we know the mass Of the sample. In this example the water starts to boil at 3.8 min And is complete at 14.5 min So we’ve added 422.4J/min For 10.7min = 4520 J Since the mass is 2 gram then Hv. = 4520/2 = 2260 J (Mass = 2 gram) Time = 3.8min 1 2 3 4 5 Time (min) Time = 14.5 min 10 11 12 132614 Cooling Curve The opposite of a heating Curve is a COOLING CURVE. Brrrrr… Since the sample is cooling it must be releasing heat. As Temp decreases KE dec and as a sample goes from gas To liquid to solid the PE must be decreasing. Instead of Heat of vaporization and heat of fusion we have the Heat of condensation and the Heat of solidification. They Are equal to Hv and Hf but are opposite in value -Hv = Hc & -Hf = Hs 27 Phase I: T dec KE dec PE constant Cooling Curve Phase II: T constant KE constant PE dec Hc = -Hv 100 80 Temp Phase III: T dec KE dec PE constant 120 Phase IV: T constant KE constant PE dec Hs = -Hf Phase V: same as I and III 60 Gas I Gas & Liquid II III IV V Liquid Condensation 40 20 Liquid & solid 0 -20 solid Solidification -40 Time Note: This is the mirror image of a heating curve 28 Cooling Curve Calculations Problem: How much heat is released when 100g Of water solidifies? How much heat is released when 100g of water condenses? a) Q = m x Hs (i.e. –Hf ) Q = 100g x -334 J/g Q = -33,400 J (i.e. 33,400 joules are released) The negative sign means this much heat is released (and not absorbed) b) Q = 100g x -2260 J/g = -226,000 J 29