* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download csa5011_distributions
Survey
Document related concepts
Transcript
Corpora and Statistical Methods
Albert Gatt
Probability distributions
Example 1: Book publishing
Case:
publishing house considers whether to publish a new textbook
on statistical NLP
considerations include: production cost, expected sales, net
profits (given cost)
Problem:
to publish or not to publish?
depends on expected sales and profits
if published, how many copies?
depends on demand and cost
Example 1: Demand & cost figures
Suppose:
book costs €35, of which:
publisher gets €25
bookstore gets €6
author gets €4
To make a decision, publisher needs to estimate profits as a
function of the probability of selling n books, for different
values of n.
profit = (€25 * n) – overall production cost
Terminology
Random variable
In this example, the expected profit from selling n books is our
random variable
It takes on different values, depending on n
We use uppercase (e.g. X) to denote the random variable
Distribution
The different values of X (denoted x) form a distribution.
If each value x can be assigned a probability (the probability of making
a given profit), then we can plot each value x against its likelihood.
Definitions
Random variable
A variable whose numerical value is determined by chance. Formally, a
function that returns a unique numerical value determined by the outcome
of an uncertain situation.
Can be discrete (our exclusive focus) or continuous
Probability distribution
For a discrete random variable X, the probability distribution p(x) gives the
probabilities for each value x of X.
The probabilities p(x) of all possible values of X sum to 1.
The distribution tells us how much out of the overall probability space (the
“probability mass”), each value of x takes up.
Tabulated probability distribution
No. copies sold
Prod. cost
Profits
(X)
Probability
P(x)
5,000
£275,000
-£150,000
.20
10,000
£300,000
-£50,000
.40
20,000
£350,000
£150,000
.25
30,000
£400,000
£350,000
.10
40,000
£450,000
£550,000
.05
Plotting the distribution
Uses of a probability distribution
Computation of:
mean: the expected value of X in the long run
based on the specific values of X, and their probability
NB: NOT interpreted as value in a sample of data, but expected
(future) value based on sample.
standard deviation & variance: the extent to which actual values of X
will differ from the mean
skewness: the extent to which our distribution is “balanced”, i.e.
whether it’s symmetrical
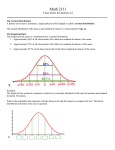
In graphics…
Mean: expected value
in the long run
SD & variance:
How much actual values
deviate from mean overall
Skewness:
Symmetry or “tail”
of our distribution
Measures of expectation and variation
The expected value (mean)
The expected value of a discrete random variable X, denoted
E[X] or μ, is a weighted average of the values of X
weighted, because not all values x will have the same probability
estimated by summing, for all values of X, the product of x and its
probability p(x)
E[ X ]
xp( x)
x
More on expected value
The mean or expected value tells us that, in the long run, we
can expect X to have the value μ.
E.g. in our example, our book publisher can expect longterm profits of:
(-150,000 * .2) + (-50,000 * .4) + (150,000 * .25) +
(350,000 * .1) +
(550,000 * .05)
= €50,000
Variance
Mean is the expected value of X, E[X]
Variance (σ2) reflects the extent to which the actual
outcomes deviate from expectation (i.e. from E[X])
σ2 = E[(X – μ)2] = Σ(x – μ)2p(x)
i.e. the weighted sum of deviations squared
Reasons for squaring:
eliminates the distinction between +ve and –ve
makes it exponential: larger deviations are given more importance
e.g. one deviation of 10 is as large as 4 deviations of 5
Standard deviation
Variance gives overall dispersion or variation
Standard deviation (σ) is the dispersion of possible outcomes;
it indicates how spread out the distribution is.
estimated as square root of variance
2
2
(
x
)
p( x)
x
The book publishing example again
Recall that for our new book on stat NLP, expected profit is
£50,000
What’s the standard deviation?
need to estimate (50000-x)2 for all x
multiply by p(x) in each case
take the square root of the result
This is left as an exercise…
Skewness
The mean gives us the “centre” of a distribution.
Standard deviation gives us dispersion.
Skewness (denoted γ “gamma”) is a measure of the symmetry
of the outcomes.
(x )
x
3
3
Skewness, continued
The formula calculates the average value of cubed deviations by the standard
deviation cubed.
Why cubed?
The cube of a positive deviation is itself positive; that of a negative is itself
negative. We want both, as we want to know deviations both to the left (-ve)
and right (+ve) of the mean.
Like the variance estimation, this emphasises large deviations in either
direction (it’s exponential).
If the outcomes are symmetrical around the mean, then +ve and –ve
deviations are balanced, and skewness is 0.
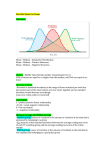
Graphical display of skewness
Positive skewness:
tail going right
Negative skewness:
tail going left
Skewness and language
By Zipf’s law (next week), word frequencies do not cluster
around the mean.
There are a few highly frequent words (making up a large proportion
of overall word frequency)
There are many highly infrequent words (f = 1 or f = 2)
So the Zipfian distribution is highly skewed.
We will hear more on the Zipfian distribution in the next lecture.
The concept of information
What is information?
Main ingredient:
an information source, which “transmits” symbols from a finite
alphabet S
every symbol is denoted si
we call a sequence of such symbols a text
assume a probability distribution s.t. every si has probability p(si)
Example:
a dice is an information source; every throw yields a symbol from the
alphabet {1,2,3,4,5,6}
6 successive throws yield a text of 6 symbols
Quantifying information
Intuition:
the more probable a symbol is, the less information it yields
“something seen very often is not very surprising”
So information is the inverse probability of the symbol
I ( si ) log b
1
log p( si )
p ( si )
for some b > 1. Usually we use base 2
Another term for I(s) is surprisal
Properties of I
1.
Non-negative
2.
If p(s) = 1, I(s) = 0
3.
If 2 events s1, s2 are independent, then:
I (si , s2 ) I ( p(s1 ) p(s2 )) I (s1 ) I (s2 )
4.
Monotonic: slight changes in probability result in slight
changes in I
Aggregate measure of information
What is the information content of a text (sequence of
symbols)?
1.
this is the same as finding the average information of a random
variable
the measure is called Entropy, denoted H
Define X as a random variable over the symbols in our
alphabet
P(s) = P(X=s) for all s in our alphabet
2.
Estimate H(P)
Entropy
The entropy (or information) of a probability distribution is
1
H b ( P) P( s) log b
P( s) log b P( s)
P( s )
sS
sS
entropy is the expected value (mean) of the surprisal
the value is interpreted as the number of “bits” of information
Entropy example
Source = an 8-sided die
Alphabet S = {1,2,3,4,5,6,7,8}
every si has p = 1/8
8
8
1
1
1
H ( P) p ( si ) log p ( si ) log log log 8 3
8
8
i 1
i 1 8
Interpretation of entropy
The information contained in the distribution P (the more
unpredictable the outcomes, the higher the entropy)
The message length if the message was generated according to
P and coded optimally
Interpretation cont/d
For the 8-sided die example, the result H(P)=3 tells us we need 3
bits on average to “transmit” the result of rolling an 8-sided die:
1
2
3
4
5
6
7
8
001 010 011 100 101 110 111 000
We can’t do it in less than 3 bits
Entropy for multiple variables
So far we have dealt with a single random variable
The joint entropy of a pair of RVs:
1
H ( X , Y ) P( x, y ) log b
P ( x, y )
xX yY
P( x, y ) log b P( x, y )
xX yY
Conditional Entropy
Given X and Y, how much information about Y do we gain if we
know X?
a version of entropy using conditional probability: H(Y|X)
H (Y | X )
P( x) H (Y | X
x X
x)
P ( x) P ( y | x) log P ( y | x)
x X
yY
P ( x) P ( y | x) log P ( y | x)
x X yY
Mutual information
Mutual information
Just as probability can change based on posterior knowledge,
so can information.
Suppose our distribution gives us the probability P(a) of
observing the symbol a.
Suppose we first observe the symbol b.
If a and b are not independent, this should alter our
information state with respect to the probability of observing
a.
i.e. we can compute p(a|b)
Mutual info between two symbols
The change in our information about a on observing b is:
1
1
log
I (a; b) log
P(a )
P ( a | b)
P ( a | b)
log
P(a)
If a and b are completely independent, I(a;b)=0.
Averaging mutual information
We want to average mutual information between all values of a
random variable A and those of a random variable B.
P ( a | b) I ( a ; b)
I ( A; b)
i
i
i
i
P ( ai | b )
P(ai | b) log
P ( ai )
And similarly:
I (a; B)
j
P(bi | a)
P(a | b j ) log
P(b j )
Combining the two…
I ( A; B)
P(a ) I (a ; B)
i
i
i
P ( ai , b j )
P(ai , b j ) log
P(ai ) P(b j )
i
j
I ( B; A)
Thus, mutual info involves taking the joint probability and
dividing by the individual probabilities.
I.e. a comparison of the likelihood of observing a, b together
vs. separately.
Mutual Information: summary
Gives a measure of reduction in uncertainty about a random
variable X, given knowledge of Y
quantifies how much information about X is contained in Y
Some more on I(X;Y)
In statistical NLP, we often calculate pointwise mutual
information
this is the mutual information between two points on a
distribution
I(x;y) rather than I(X;Y)
used for some applications in lexical acquisition
Mutual Information -- example
Suppose we’re interested in the collocational strength of two
words x and y
e.g. bread and butter
mutual information quantifies the likelihood of observing x and y
together (in some window)
If there is no interesting relationship, knowing about bread
tells us nothing about the likelihood of encountering butter
Here, P(x,y) = P(x)P(y) and I(x;y) = 0
This is the Church and Hanks (1991) approach.
NB. The approach uses pointwise MI