Download 3.2 Vector Addition and Subtraction

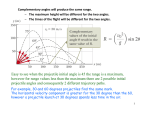
Lecture Outline
Chapter 3
College Physics, 7th Edition
Wilson / Buffa / Lou
© 2010 Pearson Education, Inc.
Chapter 3
Motion in Two Dimensions
© 2010 Pearson Education, Inc.
Units of Chapter 3
• Components of Motion
• Vector Addition and Subtraction
• Projectile Motion
• Relative Velocity
© 2010 Pearson Education, Inc.
3.1 Components of Motion
• Motion in a straight line indicates only 1
axis needed.
• What if motion is not in a straight line?
– What do we do?
3.1 Components of Motion
An object in motion on a plane can be located
using two numbers—the x and y coordinates of its
position. Similarly, its velocity can be described
using components along the x- and y-axes.
© 2010 Pearson Education, Inc.
3.1 Components of Motion
The velocity components are:
Why does the x component use cos? y
use sin?
The magnitude of the velocity vector is:
© 2010 Pearson Education, Inc.
3.1 Components of Motion
The components of the displacement are then
given by:
*Note that the x- and y-components are
calculated separately.
© 2010 Pearson Education, Inc.
3.1 Components of Motion
• Example #1:
– If a diagonally moving ball has a constant
velocity of 0.50 m/s at an angle of 37 degrees
relative to the x axis, find how far it travels in
3.0s by using x and y components of its
motion.
3.1 Components of Motion
The equations of motion are:
What do these
equations
have in
common with
our kinematic
equations?
When solving two-dimensional kinematics
problems, each component is treated
separately. The time is common to both.
© 2010 Pearson Education, Inc.
3.1 Components of Motion
If an object is initially moving
with constant velocity and
experiences acceleration in the
direction of or opposite….
If the acceleration is not
parallel to the velocity,
the object will move in a
curve: (aka…)
© 2010 Pearson Education, Inc.
Figure 3.2
3.1 Components of Motion
• Example #1:
– Suppose that the ball in Figure 3.2 has an
initial velocity of 1.50 m/s along the x axis.
Starting at t = 0, the ball receives an
acceleration of 2.80 m/s2 in the y direction.
• A.) What is the position of the ball 3.00s after t=0?
• B.) What is the resultant velocity of the ball at that
time?
3.2 Vector Addition and Subtraction
• Vector Addition is……..
• Also called Vector Sum
• Product is called the Resultant
• You’ve been doing this already, you just don’t know it….when
we add/subtract displacements
3.2 Vector Addition and Subtraction
Geometric methods of vector addition
Triangle method: [We learned it last year as…]
© 2010 Pearson Education, Inc.
3.2 Vector Addition and Subtraction
The negative of a vector has the same
magnitude but is opposite in direction to the
original vector. Adding a negative vector is the
same as subtracting a vector.
© 2010 Pearson Education, Inc.
Question 3.1a
If two vectors are given
Vectors I
a) same magnitude, but can be in any
direction
such that A + B = 0, what b) same magnitude, but must be in the same
direction
can you say about the
magnitude and direction
of vectors A and B?
c) different magnitudes, but must be in the
same direction
d) same magnitude, but must be in opposite
directions
e) different magnitudes, but must be in
opposite directions
3.2 Vector Addition and Subtraction
Vector Components and the Analytical
Component Method
If you know A and B,
here is how to find C:
Magnitude Angle Form
© 2010 Pearson Education, Inc.
3.2 Vector Addition and Subtraction
The components
of C are given by:
Equivalently,
© 2010 Pearson Education, Inc.
Question 3.2a
Vector Components I
a) it doubles
If each component of a
vector is doubled, what
happens to the angle of
that vector?
b) it increases, but by less than double
c) it does not change
d) it is reduced by half
e) it decreases, but not as much as half
Question 3.3
Vector Addition
You are adding vectors of length
20 and 40 units. What is the only
possible resultant magnitude that
you can obtain out of the
following choices?
a) 0
b) 18
c) 37
d) 64
e) 100
3.2 Vector Addition and Subtraction
Vectors can also be written using unit vectors:
© 2010 Pearson Education, Inc.
3.2 Vector Addition and Subtraction
Vectors can be resolved into components and
the components added separately; then
recombine to find the resultant.
© 2010 Pearson Education, Inc.
3.2 Vector Addition and Subtraction
3.2 Vector Addition and Subtraction
This is done most easily if all vectors start at the
origin.
© 2010 Pearson Education, Inc.
3.2 Vector Addition and Subtraction
• Apply the component method to the
addition of vectors for the Figure in the
previous slide.
• Finally, determine the magnitude of the
resultant velocity as well as the angle.
3.3 Projectile Motion
• Projectile motion is 2-D motion of an
object that is thrown or projected by some
means.
– When an object is projected, it is in free fall.
– Suppose you throw an object horizontally with
an initial velocity.
• Is there a vertical acceleration?
• Is there a horizontal acceleration?
• What if no gravity??
Question 3.4a
A small cart is rolling at
constant velocity on a flat
track. It fires a ball straight
up into the air as it moves.
After it is fired, what happens
to the ball?
Firing Balls I
a) it depends on how fast the cart is
moving
b) it falls behind the cart
c) it falls in front of the cart
d) it falls right back into the cart
e) it remains at rest
Question 3.4b
Now the cart is being pulled
along a horizontal track by an
external force (a weight
hanging over the table edge)
and accelerating. It fires a ball
straight out of the cannon as it
moves. After it is fired, what
happens to the ball?
Firing Balls II
a) it depends upon how much the
track is tilted
b) it falls behind the cart
c) it falls in front of the cart
d) it falls right back into the cart
e) it remains at rest
3.3 Projectile Motion
One object dropped
vertically (red) and
another object
projected horizontally
(yellow).
What do you observe
from the picture?
3.3 Projectile Motion
An object projected
horizontally has an
initial velocity in the
horizontal direction,
and acceleration (due
to gravity) in the
vertical direction. The
time it takes to reach
the ground is the same
as if it were simply
dropped.
© 2010 Pearson Education, Inc.
3.3 Projectile Motion
• Example #1:
– Suppose the ball from the Figure in the
previous slide is projected from a height of
25.0 m above the ground and is thrown with
an initial horizontal velocity of 8.25 m/s.
• A.) How long is the ball in flight before striking the
ground?
• B.) How far from the building does the ball strike
the ground?
3.3 Projectile Motion
A projectile launched in an arbitrary direction
may have initial velocity components in both
the horizontal and vertical directions, but its
acceleration is still downward.
© 2010 Pearson Education, Inc.
3.3 Projectile Motion
• Look at arbitrary angle with golfer in
previous slide.
• The initial velocity is resolved into its
components:
– Vxo =
– Vyo =
– Vx =
– Vy =
Question 3.5
You drop a package from
a plane flying at constant
speed in a straight line.
Without air resistance, the
package will:
Dropping a Package
a) quickly lag behind the plane
while falling
b) remain vertically under the
plane while falling
c) move ahead of the plane while
falling
d) not fall at all
Question 3.6a
Dropping the Ball I
a) the “dropped” ball
From the same height (and
at the same time), one ball
is dropped and another ball
is fired horizontally. Which
one will hit the ground
first?
b) the “fired” ball
c) they both hit at the same time
d) it depends on how hard the ball
was fired
e) it depends on the initial height
Question 3.6c
Dropping the Ball III
a) just after it is launched
A projectile is launched
from the ground at an
angle of 30°. At what
point in its trajectory does
this projectile have the
least speed?
b) at the highest point in its flight
c) just before it hits the ground
d) halfway between the ground and
the highest point
e) speed is always constant
3.3 Projectile Motion
• Example:
– Suppose a golf ball is hit off the tee with an
initial velocity of 30.0 m/s at an angle of 35
degrees to the horizontal (like Figure from 2
slides ago)
• A.) What is the maximum height reached by the
ball?
• B.) What is its range?
3.3 Projectile Motion
•
Consider two balls, both thrown
with the same initial speed vo,
but one at an angle of 45
degrees above the horizontal
and one below. Determine
whether, upon reaching the
ground,
– A.) The ball projected
upward will have the greater
speed.
– B.) The ball projected
downward will have the
greater speed.
– C.) Both balls will have the
same speed.
© 2010 Pearson Education, Inc.
3.3 Projectile Motion
The range of a projectile is maximum (if there is no
air resistance) for a launch angle of 45°.
© 2010 Pearson Education, Inc.
3.3 Projectile Motion
With air resistance, the range is shortened,
and the maximum range occurs at an angle
less than 45°. [Reduced speed = reduced
range]
© 2010 Pearson Education, Inc.
3.3 Projectile Motion
• A hockey player hits a “slap shot” in practice (with no goalie
present) when he is 15.0 m directly in front of the net. The net is
1.20 m high, and the puck is initially hit an angle of 5.00 degree
above the ice with a speed of 35.0 m/s.
• A.) Determine whether the puck makes it into the net.
3.4 Relative Velocity
• Velocity is not an absolute quantity. Rather
it is dependent upon the observer.
• Its description is relative to the observer’s
state of motion.
• Motion of objects are described as being
relative to Earth. Which we call a…)
• Measurements are usually made with
respect to some reference.
3.4 Relative Velocity
Velocity may be
measured in any
inertial reference
frame. At top, the
velocities are
measured relative to
the ground; at
bottom they are
measured relative to
the white car.
© 2010 Pearson Education, Inc.
3.4 Relative Velocity
In two dimensions, the components of the velocity,
and therefore the angle it makes with a coordinate
axis, will change depending on the point of view.
© 2010 Pearson Education, Inc.
Review of Chapter 3
• Two-dimensional motion is analyzed by
considering each component separately. Time is
the common factor.
© 2010 Pearson Education, Inc.
Review of Chapter 3
• Vector components:
• In projectile motion, the horizontal and
vertical motions are determined
separately.
© 2010 Pearson Education, Inc.
Review of Chapter 3
• Range is the maximum horizontal distance
traveled.
• Relative velocity is expressed relative to a
particular reference frame.
© 2010 Pearson Education, Inc.