Download chapter 7 review

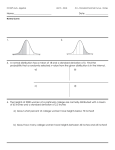
CHAPTER 7 REVIEW
The following questions are in a True/False format. The answers to these questions will frequently depend on
remembering facts, understanding of the concepts, and knowing the statistical vocabulary. Before answering
these questions, be sure to read them carefully!
33) A random variable is discrete if the value of the random variable depends upon the outcome of a chance
experiment.
ANS: False
34) A random variable is continuous if the set of possible values includes an entire interval on the number line.
ANS: True
35) For a discrete random variable x,
.
ANS: True
36) For a discrete random variable,
.
ANS: False
37) Using the notation C = continuous and D = discrete, indicate whether each of the random variables are discrete
or continuous.
a)
The number of defective lights in your school's main hallway
b)
The barometric pressure at midnight
c)
The number of staples left in a stapler
d)
The number of sentences in a short story
e)
The average oven temperature during the cooking of a turkey
f)
The number of lightning strikes during a thunderstorm
ANS: a) D b) C c) D d) D e) C f) D
38) The famous physicist, Ernest Rutherford, was a pioneer in the study of radioactivity using electricity. In one
experiment he observed the number of particles reaching a counter during time 1700 intervals of 7.5 seconds each.
The number of intervals that had 0 - 4 particles reaching the counter is given in the table below.
k particles
0
1
2
3
4
Number of time
intervals with k
particles
57
203
383
525
532
Let the random variable x = number of particles counted in a 7.5 second time period.
a)
Fill in the table below with the estimated probability distribution of x, and sketch a
probability histogram for x.
Probability distribution
x
0
1
2
3
4
P(x)
Probability histogram
b)
Using the estimated probabilities in part (a), estimate the following:
i)
P(x = 1), the probability that 1 particle was counted in 7.5 seconds.
ii)
P(x < 3), the probability that fewer than 3 particles were counted.
iii)
P(x  3), the probability that at least 3 particles were counted.
ANS:
a)
Probability Distribution:
Histogram: Number of particles
b)
i)
ii)
iii)
P(x = 1) = 0.1194
P(x < 3) = 0.3782
P(x  3) = 0.6218
39) The sales of a newsmagazine vary from week to week, depending on the importance of the news of the
previous week. From empirical data over many years, the following distribution of sales (rounded to the nearest
million) has been carefully constructed. What are the mean and standard deviation of this distribution?
X
P(X)
0
0.15
1
0.25
2
0.40
3
0.20
ANS:
x
x
= (1.65)2(0.15) + (0.65)2(0.25) + (0.35)2(0.40) + (1.35)2(0.20)
= 0.9631
40) Determine the following areas under the standard normal (z) curve.
a)
The area under the z curve to the left of 2.53
b)
The area under the z curve to the left of 1.33
c)
The area under the z curve to the right of 0.76
d)
The area under the z curve to the right of 1.47
e)
The area under the z curve between 1 and 3
f)
The area under the z curve between 2.6 and 1.2
ANS:
a)
b)
c)
d)
e)
f)
0.9943
0.0918
0.2236
0.9292
0.8400
0.1104
41) A gasoline tank for a certain model car is designed to hold 12 gallons of gas. Suppose that the actual capacity
of the gas tank in cars of this type is well approximated by a normal distribution with mean 12.0 gallons and
standard deviation 0.2 gallons. What is the probability that a randomly selected car of this model will have a gas
tank that holds at most 11.7 gallons?
ANS:
42) The owners of the Burger Emporium are looking for new supplier of onions for their famous hamburgers. It is
important that the onion slice be roughly the same diameter as the hamburger patty. After careful analysis, they
determine that they can only use onions with diameters between 9 and 10 cm. Company A provides onions with
diameters that are approximately normally distributed with mean 10.3 cm and standard deviation of 1.2 cm.
Company B provides onions with diameters that are approximately normally distributed with mean 10.6 cm and
standard deviation of 0.9 cm. Which company provides the higher proportion of usable onions? Justify your choice
with an appropriate statistical argument.
ANS: The onions from Company A will be between 9 and 10 cm diameter with probability
.
The onions from Company B will be between 9 and 10 cm diameter with probability
.
There are a greater proportion of the onions from Company A that are the correct size.
43) The time that it takes a randomly selected employee to perform a certain task is approximately normally
distributed with a mean value of 120 seconds and a standard deviation of 20 seconds. The slowest 10% (that is, the
10% with the longest times) are to be given remedial training. What times qualify for the remedial training?
ANS: To qualify for remedial training, the time would be greater than or equal to the highest 10% of the times.
. Solve
to get x > 145.6.
44) While playing Monopoly, Andi estimated the probabilities of the non-zero rents according to the following
probability distribution:
x
P(x)
$2
0.40
$14
0.20
$20
0.20
$100
0.20
Consider the random variable x = dollar amount in rent collected in a Monopoly roll.
a)
If the table above specifies the probability distribution of x, what is the mean of the random
variable x?
b)
If the probabilities are associated with the outcomes as in the table above, what is the
standard deviation of the random variable x?
ANS:
a)
b)
45) At the last home football game, the senior football players walk through a specially constructed welcoming
arch, 2 abreast. It is considered unseemly to bump each other on the way through, so the arch must be wide enough
for two players to go through. The distribution of widths of football players with shoulder pads on is approximately
normal; the mean padded football player width is 30 inches, and the standard deviation is 5 inches. Let random
variable w = width in inches of a randomly selected padded football player.
a)
Since this is a statistics test, the carpenter who will be constructing the arch has only metric
measuring tools, and must convert all the information above to metric measures. 1 inch =
2.54 centimeters, and we define random variable m = width in centimeters of a randomly
selected padded football player. What are the mean and standard deviation of m?
b)
Suppose the football players are paired randomly to go through the arch. Define random
variable v = w1 + w2 to be the collective width (in inches) of two randomly selected football
players. What are the mean and standard deviation of v?
c)
Suppose that in the original specifications of the arch a 10 inch separation of the football
players is specified so that the football players have room to avoid each other. This leads to
random variable a = 10 + w1 + w2. Describe how this addition of 10 inches of "wiggle
room" would change the mean and standard deviation in part (b). Do not recalculate the
mean and standard deviation.
ANS:
a)
b)
c)
The mean would increase by 10". [to 70"]
The standard deviation would remain unchanged. [7.07"]