Download Cosmological Structure Formation A Short Course

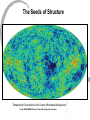
Cosmological Structure
Formation
A Short Course
II. The Growth of Cosmic Structure
Chris Power
Recap
• The Cold Dark Matter model is the standard
paradigm for cosmological structure formation.
• Structure grows in a hierarchical manner -- from
the “bottom-up” -- from small density
perturbations via gravitational instability
• Cold Dark Matter particles assumed to be nonthermal relics of the Big Bang
Key Questions
• Where do the initial density perturbations come from?
• Quantum fluctuations imprinted prior to cosmological
inflation.
• What is the observational evidence for this?
• Angular scales greater than ~1° in the Cosmic Microwave
Background radiation.
• How do these density perturbations grow in to the
structures we observe in the present-day Universe?
• Gravitational instability in the linear- and non-linear regimes.
Cosmological Inflation
•
Occurs very early in the history
of the Universe -- a period of
exponential expansion, during
which expansion rate was
accelerating
d 2a
0
2
or alternatively,
dt during which
comoving Hubble length is a
decreasing function of time

d(H 1 /a)
0
dt
Cosmological Inflation
• Prior to inflation, thought that the Universe was in a “chaotic”
state -- inflation wipes out this initial state.
• Small scale quantum fluctuations in the vacuum “stretched out”
by exponential expansion -- form the seeds of the primordial
density perturbations.
• Can quantify the “amount” of inflation in terms of the number of
e-foldings it leads to
a(t end )
N(t)  ln
a(t)
Cosmological Inflation
•
Turns out the ~70 e-foldings are required to solve the so-called
classical cosmological problems
•
•
•
•
Flatness
Horizon
Abundance of relics -- such as magnetic monopoles
Homogeneity and Isotropy
•
Inflation thought to be driven by a scalar field, the inflaton -- could it
also be responsible for the accelerated expansion (i.e. dark energy) we
see today?
•
Turns out that angular scales larger than ~1º in the CMB are relevant
for testing inflation -- also expect perturbations to be Gaussian.
The Seeds of Structure
Temperature Fluctuations in the Cosmic Microwave Background
Credit: NASA/WMAP Science Team (http://map.gsfc.nasa.gov)
Temperature and Density
Pertubations
•
•
CMB corresponds to the last scattering surface of the radiation -- prior to
recombination Universe was a hot plasma -- at z~1400, atoms could
recombine.
Temperature variations correspond to density perturbations present at this
time -- the Sachs-Wolfe effect:
T
 a 
 2  2
T c
a 3c
Characterising Density
Perturbations
•
We define the density at
location x at time t by
(x,t)  ( t)
( t) in
• This can be expressed
 (x,t) 
terms of its Fourier
components

•

ˆ( k,t) e ikx
(x,t)   
k
Inflation predicts
that  can
be characterised as a
Gaussian random field.
Gaussian Random Fields
•

The properties of a Gaussian
Random Field can be
completely specified by the
correlation function
 (r)   (r) (r  x)
•
Common to use its Fourier
transform, the Power Spectrum
•
Expressible
P(k)  as| 
k
|2
P(k)  Ak n T(k)2

Aside : Setting up Cosmlogical
Simulations
• Generate a power spectrum
-- this fixes the dark matter
model.
• Generate a Gaussian
Random density field using
power spectrum.
• Impose density field d(x,y,z)
on particle distribution -- i.e.
assignment displacements
and velocities to particles.
Linear Perturbation Theory
• Assume a smooth background -- how do small perturbations
to this background evolve in time?
• Can write down
• the continuity equation
• the Euler equation

• Poisson’s equation

D
 .v
Dt
Dv
p

 
Dt

  4G
Linear Perturbation Theory
• Find that
• the continuity equation leads to
d
 .v
dt
• the Euler equation leads to

dv
p
 Hv 
 
dt
0
• Poisson’s equation leads to

  4G0
Linear Perturbation Theory
• Combine these equations to obtain the growth
equation
d 2
d
c s2 2
 2H
 4 G0  2
2
dt
dt
a
• Can take Fourier transform to investigate how
different modes grow

d 2k
dk
c s2 k 2k
 2H
 4G0k 
2
dt
dt
a2
Linear Perturbation Theory
• Linear theory valid provided the size of perturbations is small -<<1
• When ~1, can no longer trust linear theory predictions -problem becomes non-linear and we enter the “non-linear”
regime
• Possible to deduce the approximate behaviour of perturbations
in this regime by using a simple model for the evolution of
perturbations -- the spherical collapse model
• However, require cosmological simulations to fully treat
gravitational instability.
Next Lecture
• The Spherical Collapse Model
• Defining a dark matter halo
• The Structure of Dark Matter Haloes
• The mass density profile -- the Navarro, Frenk & White
“universal” profile
• The Formation of the First Stars
• First Light and Cosmological Reionisation
Some Useful Reading
• General
• “Cosmology : The Origin and Structure of the Universe” by
Coles and Lucchin
• “Physical Cosmology” by John Peacock
• Cosmological Inflation
• “Cosmological Inflation and Large Scale Structure” by Liddle
and Lyth
• Linear Perturbation Theory
• “Large Scale Structure of the Universe” by Peebles