Download 17 Oct 08 - Seattle Central College

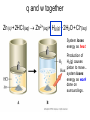
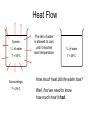
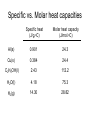
Plan for Fri, 17 Oct 08
• Lecture
– Main points of 6.1
• System vs. surroundings
• Kinetic vs. potential energy
• Work vs. heat
– Enthalpy and Calorimetry (6.2)
• Quiz 3
Thermodynamic Talking Points
• Energy of the universe is constant, but it is not
uniformly distributed.
• We can monitor the changes in energy due to
physical or chemical processes by artificially
partitioning the universe into a “system” and its
“surroundings.”
• The energy content of a system is partitioned
into:
– Kinetic: the energy of an object in motion
– Potential: the energy of an object derived from its
location in a field of force
Thermodynamic Talking Points
• Energy can be exchanged between the system and
surroundings in two main ways:
– Heat (q): energy flow between objects due to a temperature
difference.
• Heat is a transfer of energy manifested by changes in the
microscopic thermal motions of particles
• Changes in vibrations, rotations and translations of molecules
• Changes in bonding patterns
– Work (w): energy acting over a distance that results in the
movement of an object.
• Work is an energy transfer manifested by changes in the
macroscopic physical variables of a system.
• To accelerate a baseball from 0 mph to 60 mph, we must perform
work on it.
q without w
• If we run an experiment in
which the volume is fixed,
then
w = -PDV = 0
 DE = q + 0
• Combustion produces
gaseous products.
• If we don’t allow the
gaseous products to
change their volume, the
energy lost by the system
is in terms of heat only.
C(s) + O2(g)  CO2(g) + heat
w without q
• If we run an experiment in
which the volume is
allowed to change, but no
heat transfer is allowed,
then
q=0
 DE = w
• Isothermal expansion of a
gas only loses energy as Some energy is expended by
work.
the system to push back the
• Is any PV-work done if the atmosphere as it expands.
gas expands into a
vacuum?
q and w together
Zn (s) + 2HCl (aq)  Zn2+(aq) + H2 (g) + 2H2O + Cl-(aq)
System loses
energy as heat.
Production of
H2(g) causes
piston to move...
system loses
energy as work
done on
surroundings.
q, PV work, and non-PV work
The combustion of fuel in the
space shuttle results in:
1. The emission of heat (q)
2. The expansion of the system against
constant atmospheric pressure (PVwork)
3. The rapid movement of the shuttle over
a distance (non-PV-work)
If we could keep the shuttle from moving as
its fuel combusted, what would happen to
this non-PV-work energy?
 It would be transferred as heat to the surroundings.
Internal Combustion
Engine
1. Intake. Mixture of air and gas enters
combustion chamber.
2. Compression. The mixtures are placed
under pressure.
3. Combustion/Expansion. Spark ignites
the mixture, resulting in rapid production of
gaseous products and heat. The hot mixture
expands, pressing on and moving parts of
the engine and performing useful work.
4. Exhaust. The cooled combustion
products are exhausted.
Four-stroke cycle
1. Intake
2. compression
3. power
4. exhaust
Work
• There really isn’t anything useful about PV-work…it is
simply an accounting of the energy required to change
the volume of your system against constant external
pressure.
• In this way, the combustion of gas in your car, even
though it results in the production of gases, is not PVwork…
• The volume change in the system relative to the amount
of gas produced is so small that the pressure does not
remain constant.
• Useful work comes from a clever partitioning of the heat
energy (the enthalpy), which you will learn about in 162
(HAND-WAVING ALERT).
Heat vs. Temperature
q
Temperature is an
index of the
average molecular
KE.
Heat is an
exchange of
energy due to a
temperature
difference.
Go to Slide Show View (press F5) to play the video or animation. (To exit, press Esc.)
This media requires PowerPoint® 2000 (or newer) and the Macromedia Flash Player (7 or higher).
[To delete this message, click inside the box, click the border of the box, and then press delete.]
Copyright © Houghton Mifflin Company. All rights reserved.
Heat vs. Temperature
• Add 100 J of heat to a collection of 100 water molecules.
• Add 100 J of heat to a collection of 1,000,000 water molecules.
• Which system will exhibit the greatest increase in T?
– The collection of 100 water molecules.
– Same amount of heat delivered, different average velocities, different
final temperatures.
• An extensive physical property depends directly on
the amount of substance present.
– Examples: enthalpy, mass, volume, length
• An intensive physical property is not related to the
amount of substance.
– Examples: temperature, density, concentration, color
Measuring DE
We would like to know about the internal energy change
accompanying chemical processes:
DE  q  w
Consider a process carried out at constant P:
DE  q  w
DE  qP - PDV
The heat transferred at const P contains a “pure heat” component and
a “non-PV-work” component (HAND-WAVING ALERT)…you will
learn about this in 162.
The work term at const P represents the energy required to change
the volume of the system…this is “PV-work.”
Measuring the heat flow at const P gives you the internal energy
minus PV-work.
 qP  DE  PDV
Enthalpy vs. Internal Energy
Recall our definition of enthalpy:
H  E  PV
Recall the heat transferred at constant P:
 qP  DE  PDV
 qP  DE  PDV  DH
q p  DH
We can track the heat flow
in a process occurring at
constant P and that will give
us direct info about DE.
Enthalpy examples
• Heat transfer often accompanies physical and chemical processes.
• “Heat of Fusion” - enthalpy change associated with melting
H2O(s)  H2O(l)
DHfus = +0.334 kJ/mol ENDO
• “Heat of Vaporization” - enthalpy change associated with boiling
H2O(l)  H2O(g)
DHvap = +2.26 kJ/mol ENDO
• “Heat of Reaction” - enthalpy change associated with a chemical
reaction
CH4(g) + 2O2(g)  CO2(g) + 2H2O(g) DHrxn = -50.1 kJ/mol EXO
• “Heat of Solution” – enthalpy change associated with the
dissolution of ionic solids in water
NH4NO3(s)  NH4+(aq) + NO3-(aq)
DHsoln = +82.93 kJ/mol ENDO
CaCl2(s)  Ca2+(aq) + 2Cl-(aq)
DHsoln = -26.2 kJ/mol EXO
Example
• 5.00 g of ammonium nitrate is dissolved in
500. mL of water at 25.00oC. What is the
final temperature of the water?
NH4NO3(s)  NH4+(aq) + NO3-(aq)
DHsoln = +82.93 kJ/mol
Heat Flow
System:
1 L of water
T = 50oC
Surroundings:
T = 25oC
The liter of water
is allowed to cool,
until it reaches
room temperature.
1 L of water
T = 25oC
How much heat did the water lose?
Well, first we need to know
how much heat it had.
Heat Capacity
Heat Capacity (C):
• the energy required to raise the
temp. of a sample of a substance
by 1oC;
• the ability of a substance to
absorb heat.
• C is an extensive property
Recall: thermal energy is
associated with the random
motions of atoms and molecules
Heat capacity gives you a measure
of how much more random those
motions can get.
q  C  DT
DT  T f - Ti
Units of C: J/oC
Specific Heat
Specific heat (s): the energy
required to raise the
temperature of 1 gram of a
substance by 1oC.
You can also have molar heat
capacities.
Specific heat is an intensive
version of heat capacity (like
density is an intensive version
of mass)
If we know the specific heat of a
substance, the mass, and the
temperature change, we can
determine the heat flow.
q  s  m  DT
C
Units of s: J/oC.g
Specific Heat Specifics
• Typically, specific heats depend on:
– Degrees of freedom: the number of different motions
available to a molecule or atom
– Molar mass: bigger molecules have more bonds that
can vibrate
– Strength of intermolecular attraction: energy can
be stored in these attractions…they can vibrate too
• Compounds have higher heat capacities than
elements…how come?
– Greater complexity  more ways to store energy 
higher heat capacity
Specific vs. Molar heat capacities
Specific heat
(J/g.oC)
Molar heat capacity
(J/mol.oC)
Al(s)
0.901
24.3
Cu(s)
0.384
24.4
C2H5OH(l)
2.43
112.2
H2O(l)
4.18
75.3
H2(g)
14.30
28.82
System:
1 L of water
T = 50oC
The liter of water is
allowed to cool, until it
reaches room
temperature, 25oC.
How much heat did
the water lose?
q  s  m  DT
J
m  1 L = 1000 mL = 1000 g
s  4.184
g C
DT  T f - Ti  -50C+25C = - 25C

q  4.184 J
1000 g  -25C   -104,600 J


g C
 -104.6 kJ