Download CHAPTER 10 FACILITIES LAYOUT AND LOCATION

LESSON 20: FACILITIES LAYOUT AND
LOCATION
Outline
•
•
•
•
•
•
•
The Problem
Objective of Facility Layout
Basic Types of Layout
Product versus Process Layout
Cellular Layouts
Proximity
Assignment Problem
The Problem
• In this lesson, we shall discuss how a plant or
workplace should be laid out.
• Consider the problem of finding suitable locations for
machines, workstations, storage areas and aisles
within a plant.
• How to find suitable locations for departments,
lounges and mail rooms and labs within a building
that houses a faculty.
• The layout problem may also occur in other places
such as grocery stores, hospitals, airports, etc.
Objectives of Facility Layout
• A facility layout problem may have many objectives. In
the context of manufacturing plants, minimizing material
handling costs is the most common one.
• Other objectives include efficient utilization of
– space
– labor
• Eliminate
– bottlenecks
– waste or redundant movement
Objectives of Facility Layout
• Facilitate
– organization structure
– communication and interaction between workers
– manufacturing process
– visual control
• Minimize
– manufacturing cycle time or customer flow time
– investment
• Provide
– convenience, safety and comfort of the employees
– flexibility to adapt to changing conditions
Basic Types of Layouts
• Process Layout
– Used in a job shop for a low volume, customized
products
• Product Layout
– Used in a flow shop for a high volume, standard
products
Basic Types of Layouts
• Fixed Position Layout
– Used in projects for large products e.g., airplanes,
ships and rockets
• Cellular layouts
– A cell contains a group of machines dedicated for a
group of similar parts
– Suitable for producing a wide variety parts in
moderate volume
Product vs. Process Layouts
• A process layout is a functional grouping of machines.
For example, a group of lathe machines are arranged
in one area, drill machines in another area, grinding
machines in another area and so on. Different job
jumps from one area to another differently. Hence, the
flow of jobs is difficult to perceive. This type of layout is
suitable for a make-to-order or an assemble-to-order
production environment, as in a job shop where
customization is high, demand fluctuates, and volume
of production low. Since a wide variety of products are
produced, general purpose equipments and workers
with varied skills are needed.
Product vs. Process Layouts
• A product layout arrangement of machines. Every job
visits the machines in the same order. This type of
layout is suitable for a make-to-stock or an assembleto-stock production environment, as in a flow shop
where products are standard, demand stable, and
volume of production high. Since variety is low, special
purpose equipments and workers with a limited skill are
needed.
• Advantage
• A process layout provides flexibility
• A product layout provides efficiency.
Product vs. Process Layouts
• Inventory
• A product layout has a low work-in-process
inventory and high finished goods inventory because
production is initiated by demand forecast.
• On the other hand, a process layout has a high
work-in-process inventory and low finished goods
inventory.
• Material handling
• A product layout can use automatic guided vehicles
which travels in a fixed path. But, variable path
forklifts are suitable for a process layout.
Product vs. Process Layouts
• Scheduling/line balancing
• In case of a process layout, jobs arrive throughout
the planning period. A process layout requires
dynamic scheduling where a new scheduling
decisions is made whenever a new job arrives.
• In case of a product layout, sequencing and timing
of product flow are standard and set when the line is
designed. With a change in demand, a product
layout may need a new line balancing decision.
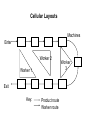
Cellular Layouts
•
•
•
Every cell contains a group of machines which are
dedicated to the production of a family of parts.
One of the problems is to identify a family parts that
require the same group of machines.
These layouts are also called as group technology
layouts.
Cellular Layouts
Machines
Enter
Worker 2
Worker 1
Exit
Key:
Product route
Worker route
Worker
3
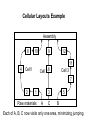
Cellular Layouts Example
Assembly
4
6
7
5
8
2
1
A
10
3
B
9
12
11
C Raw materials
Cellular Layouts Example
• The previous slide shows a facility in which three parts
A, B, C flow through the machines.
• The next slide provides the information in a matrix form
which includes some other parts D, E, F, G, H.
• The rows correspond to the parts and columns to the
machines.
• Just by interchanging rows and columns, eventually a
matrix is obtained where the “X” marks are all
concentrated near the diagonal. This matrix provides the
cells. For example, parts A, D and F require Machines 1,
2, 4, 8 and 10 which forms a cell.
Cellular Layouts Example
Parts
A
B
C
D
E
F
G
H
1 2 3 4
x x
x
x
x x
x
x
x
x
Machines
5 6 7 8 9 10 11 12
x
x
x
x
x x
x
x
x
x
x x
x
x
x
x
x
x
x x
Cellular Layouts Example
Machines
Parts 1 2 4 3 5 6 7 8 9 10 11 12
A
x x x
x
x
B
x
x
x x
C
x
x
x
D
x x x
x
x
E
x x
x
F
x
x
x
G
x
x
x
x
H
x
x x
Cellular Layouts Example
Machines
Parts 1 2 4 3 5 6 7 8 9 10 11 12
A
x x x
x
x
D
x x x
x
x
B
x
x
x x
C
x
x
x
E
x x
x
F
x
x
x
G
x
x
x
x
H
x
x x
Cellular Layouts Example
Parts
A
D
B
C
E
F
G
H
1
x
x
x
Machines
2 4 8 3 5 6 7 9 10 11 12
x x x
x
x x x
x
x
x
x x
x
x
x
x x
x
x x
x
x
x
x
x
x x
Cellular Layouts Example
Parts
A
D
F
B
C
E
G
H
1 2 4 8
x x x x
x x x x
x
x x
Machines
3 5 6 7 9 10 11 12
x
x
x
x
x
x
x x
x
x
x
x
x
x
x
x
x
x
x
Cellular Layouts Example
Parts
A
D
F
B
C
E
G
H
1
x
x
x
Machines
2 4 8 10 3 5 6 7 9 11 12
x x x x
x x x x
x x
x
x
x x
x
x
x
x x
x
x
x
x
x
x
x x
Cellular Layouts Example
Parts
A
D
F
C
G
B
E
H
1
x
x
x
Machines
2 4 8 10 3 6 9 5 7 11 12
x x x x
x x x x
x x
x x x
x x x
x
x x x x
x
x
x
x x x
Cellular Layouts Example
Assembly
8
10
9
12
11
4
Cell 2 6
Cell1
Cell 3
7
2
1
Raw materials
3
A
C
5
B
Each of A, B, C now visits only one area, minimizing jumping.
Advantages of Cellular Layouts
• Reduced material handling and transit time
• Reduced setup time
• Reduced work-in-process inventory
• Better use of human resources
• Better scheduling, easier to control and automate
Disadvantages of Cellular Layouts
• Sometimes cells may not be formed because of
inadequate part families.
• Some cells may have a high volume of
production and others very low. This results in
poorly balanced cells.
Disadvantages of Cellular Layouts
• When volume of production changes, number of
workers are adjusted and workers are
reassigned to various cells. To cope with this
type of reassignments, workers must be multiskilled and cross-trained.
• Sometimes, machines are duplicated in different
cells. This increases capital investment.
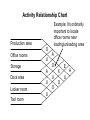
Activity Relationship Chart
•
•
An activity relationship chart is a graphical tool
used to represent importance of locating pairs
of operations near each other.
Importance is described using letter codes
defined below:
A- absolutely necessary
E- especially important
I - important
O - ordinarily important
U- unimportant
X- undesirable
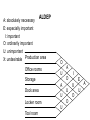
Activity Relationship Chart
Production area
O
Office rooms
Example: It’s ordinarily
important to locate
office rooms near
loading/unloading area
A
U
I
O
Storage
A
Dock area
X
U
U
U
U
O
O
Locker room
Tool room
E
A
Activity Relationship Chart
•
Sample interpretation of the diagram on the
previous slide:
• To find how important it is to locate office
rooms near loading/unloading area, find the
diamond shaped block at the intersection of
office rooms and loading/unloading area. The
block contains “O” meaning ordinarily
important. Therefore, it’s ordinarily important to
locate office rooms near loading/unloading
area.
From-To Chart
•
A from-to chart is used to analyze flow of
materials between departments. The example
below shows distances in feet. So, the distance
between Saws and Drills is 30 feet. The chart
may also show material handling trips or cost
per period.
Punch
Saws Milling Press Drills
Saws
18
40
30
Milling
18
38
75
Punch Press
40
38
22
Drills
30
75
22
Assignment Method
• Many methods can be used to solve the facility layout
problem. Here we discuss assignment method to minimize
material handling costs.
• Suppose that some machines 1, 2, 3, 4 are required to be
located in A, B, C, D. The cost of locating machines to
locations are known and shown below. For example, if
Machine 2 is located to location C, the cost is 7 (say,
hundred dollars per month).
Location
Machine
1
2
3
4
A
10
6
8
9
B
7
4
6
5
C D
6 11
7 9
5 6
3 12
Assignment Method
• The problem is to locate the machines to minimize total
material handling costs.
• One solution can be (not necessarily and optimal solution)
to assign 1, 2, 3, 4 to respectively C, B, A, D. In such a
case total cost is 6+4+8+12=30 hundred dollars per
month.
Location
Machine
1
2
3
4
A
10
6
8
9
B
7
4
6
5
C D
6 11
7 9
5 6
3 12
Assignment Method
• Notice in this solution that every machine is assigned to
one location and every location is assigned to one
machine. So, there is a single box in each row and each
column. Every solution will must this property.
• If there are more locations than machines, dummy
machines must be added with the same cost for all
locations. Assignment method finds an optimal solution.
Location
Machine
1
2
3
4
A
10
6
8
9
B
7
4
6
5
C D
6 11
7 9
5 6
3 12
Assignment Method
1. Perform row reductions
– Subtract minimum value in each row from all other row
values
2. Perform column reductions
– Subtract minimum value in each column from all other
column values
3. Line Test
– Cross out all zeros in matrix using minimum number of
horizontal & vertical lines. If number of lines equals
number of rows in matrix, optimum solution has been
found, stop.
4. Matrix Modification
– Subtract minimum uncrossed value from all uncrossed
values & add it to all cells where two lines intersect. Go
to Step 3.
Assignment Example
Location
Machine
1
2
3
4
A
10
6
8
9
Row reduction
4 1 0 5
2 0 3 5
3 1 0 1
6 2 0 9
B
7
4
6
5
C D
6 11
7 9
5 6
3 12
Column reduction
2 1 0 4
0 0 3 4
1 1 0 0
4 2 0 8
Line Test
2 1 0
0 0 3
1 1 0
4 2 0
4
4
0
8
Number lines = 3 <> 4 = number of rows. So, modify matrix
Assignment Example
• More on the previous slide:
• From rows 1, 2, 3, 4 subtract respectively 6, 4, 5, 3
which are minimum numbers on the rows. The results
are shown under row reduction.
• Next from columns A, B, C, D subtract respectively 2, 0,
0, 1 which are minimum numbers on the columns. The
results are shown under column reduction.
• Next, find minimum number of lines to cross out all the
zeros. Since the minimum number of lines = 3 < 4 =
number of rows, more computation is necessary.
Assignment Example
• A zero assignment is an assignment solution with
exactly one zero from each row and exactly one zero
from each column. After we decide to stop computation,
we find a zero assignment.
• As long as the minimum number of lines is less than the
number of rows, it’s not possible to find a zero
assignment. If the minimum number of lines equals the
number of rows, then there exists a zero assignment.
• If we mistakenly decided that the minimum number of
lines to cover all the zeros is 4, then we would stop, and
attempted to find a zero assignment with no success.
Thus, the mistake would be detected.
Assignment Example
• See the matrix under line test on Slide 34. The minimum
uncovered number is 1. There are three types of
numbers and these numbers are modified in three
different ways:
– uncovered numbers: subtract minimum uncovered
number 1 from all uncovered numbers.
– numbers covered by one line: do nothing
– numbers covered by two lines: add minimum
uncovered number 1 to all numbers covered by two
lines.
• The modified matrix is shown next.
Assignment Example
Modify matrix
Line Test
1
0
0
3
1
0
0
3
0
0
0
1
0
4
0
0
4
5
0
8
Location
Machines
1
2
3
4
A
1
0
0
3
B
0
0
0
1
C
0
4
0
0
0
0
0
1
0
4
0
0
4
5
0
8
# lines = # rows
so at optimal solution
Location
D
4 Machines A B C D
1
10 7 6 11
5
2
6 4 7 9
0
3
8 6 5 6
8
4
9 5 3 12
Total material handling costs = 22
Assignment Example
• Explanation on the previous slide:
• Another line test is done on the modified matrix. It’s
observed that the minimum number of lines = 4 =
number of rows. So, the process stops.
• Next, a zero assignment is found. See one box on each
row and one box one each column. The boxes denote
the optimal assignment.
• So, locate machine 1 to B, machine 2 to A, machine 3 to
D and machine 4 to C. To find the corresponding we
have to check with the original cost matrix. The total cost
is 7+6+6+3 = 22 hundred dollars per month.
READING AND EXERCISES
Lesson 20
Reading:
– Section 10.1-10.4 pp. 557-573 (4th Ed.), pp. 535-552
(5th Ed.)
Exercises:
– 10.1 p. 568, 10.7, p. 573 (4th ED.)
– 10.1 p. 547, 10.7, p. 552 (5th ED.)
LESSON 21: LOCATING A SINGLE FACILITY
THE RECTILINEAR DISTANCE PROBLEM
Outline
• Locating New Facilities
• Minimize Weighted Sum of the Rectilinear Distances
• Minimize Maximum Rectilinear Distance
Locating New Facilities
•
In Lessons 15-16, we consider the problem of locating
new facilities. For example, consider locating
1. a facility used by many people: a hospital, a
gymnasium, computer center, student center, etc.
2. emergency facilities: a fire station, police station, etc.
3. airline hub, utility cables such as phone cables etc.
4. a radio tower, etc.
Locating New Facilities
•
Distance is an important consideration in each of
these location problems. It’s desirable to locate a
facility that’s not too far from the users. Following are
the issues:
• How the distance will be measured
• What importance (weight) will be assigned to
various users
• Whether the location will be selected on the
basis of total (weighted) distance or the
maximum distance
Locating New Facilities
•
•
First, there are two important types of distance
measures. People walks or drives along the streets,
possibly by changing directions several times but
airplanes and radio signals travel along a straight
line without any change of directions. Utility cable
are often laid out without changing directions.
For the first type of cases, when directions are
changed more often, rectilinear distance measure is
more appropriate. On the other hand for the latter
case, when the direction is not not changed so often,
Euclidean distance measure is more appropriate.
Locating New Facilities
•
•
Suppose L(5,5) is the
location of the new
facility and A(2,1) is
location of an user.
Between A and L, the
rectilinear distance is
given by total length of
two broken lines and
Euclidean distance by
the length of the solid
line.
5
3
A(2,1)
L(5,5) Rectilinear
distance
4
Euclidean
distance
Locating New Facilities
• Notations:
• X-coordinate of user location i = ai
• Y-coordinate of user location i = bi
• Weight assigned to user location i = wi
• Location of the proposed facility = (x,y)
• For the picture shown on the previous slide, there is
only one user location. So, index i can be omitted.
We have,
a=2, b=1, x=5, y=5
Locating New Facilities
• Rectilinear distance
= distance along the x-axis +distance along the y-axis
= |x-a|+|y-b|
=
L(5,5) Rectilinear
5
distance
4
• Euclidean distance


x  a 2   y  b2
3
A(2,1)
Euclidean
distance
Locating New Facilities
•
•
Often different user locations may be assigned a
different weight to reflect their relative importance.
For the problem of locating a computer center, the
weights may be the number potential users. For the
problem of locating an airline hub, the weights may
be the number of flights per week.
The weights are important because the new facility
may be located by minimizing total weighted
distance which is a criteria used in locating facilities
used by many users, a hospital, an airline hub, etc.
Locating New Facilities
•
Sometimes, weights are not required because it may
be more important to minimize the maximum
distance which is a criterion used in locating an
emergency facility, a radio tower, etc.
Locating New Facilities
•
In summary, there are 4 important types of problems
• Rectilinear distance
• Minimize weighted total (current lesson)
• Minimize maximum (current lesson)
• Euclidean distance
• Minimize weighted total (next lesson)
• Minimize maximum (not discussed)
• Slide 2 gives application of each type of
problems
Example
Locating New Facilities
• The new health-watch facility is targeted to serve five
census tracts in Erie, Pennsylvania. Coordinates for
the center of each census tract, along with the
projected populations, measured in thousands are
shown next. Customers will travel from the five
census tract centers to the new facility when they
need health care.
Example
Locating New Facilities
Census Tract
A
B
C
D
E
(ai,bi)
(2.5,4.5)
(3.0,2.5)
(5.5,4.0)
(5.0,2.0)
(8.0,5.0)
Population, wi
2
5
10
7
12
Minimize Weighted Sum of the
Rectilinear Distances
•
•
•
Firs, we shall discuss the problem of finding a facility
location by minimizing the weighted sum of the
rectilinear distances from the new facility to all users.
Application: locating facilities used by many people.
First, the procedure will be discussed. Then, the
procedure will be illustrated with an example.
Minimize Weighted Sum of the
Rectilinear Distances
• Find the optimal value of x as follows:
– Arrange the x-coordinates in ascending order
– Compute the cumulative weights
– The optimal value of x is obtained by dividing the
total weight by 2 and finding the first location at
which the cumulative weight equals or exceeds
this value.
Minimize Weighted Sum of the
Rectilinear Distances
• Find the optimal value of y similarly:
– Arrange the y-coordinates in ascending order
– Compute the cumulative weights
– The optimal value of y is obtained by dividing the
total weight by 2 and finding the first location at
which the cumulative weight equals or exceeds
this value.
Example: Minimize Weighted Sum of
Rectilinear Distances
Census
Tract
A
B
D
C
E
(ai,bi)
(2.5,4.5)
(3.0,2.5)
(5.0,2.0)
(5.5,4.0)
(8.0,5.0)
Weight, wi
Cumulative
Weight
Example: Minimize Weighted Sum of
Rectilinear Distances
Census
Tract
D
B
C
A
E
(ai,bi)
(5.0,2.0)
(3.0,2.5)
(5.5,4.0)
(2.5,4.5)
(8.0,5.0)
Weight, wi
Cumulative
Weight
Example: Minimize Weighted Sum of
Rectilinear Distances
• The optimal location (x,y) is (5.5,4.0). In this case,
both x and y are taken from the same location C. It
may also happen that optimal x corresponds to one
location and optimal y corresponds to some other.
• To get the optimal value, compute the weighted sum
of the rectilinear distances from (5.5, 4.0) to each
location. This is done on the next two slides.
Example: Minimize Weighted Sum of
Rectilinear Distances
Weighted sum of the rectilinea r distances
From optimal location (5.5,4.0) to 5 locations
5
  wi  5.5  ai  4.0  bi
i 1


Example: Minimize Weighted Sum of
Rectilinear Distances
Continues from the previous slide
Minimize Maximum
Rectilinear Distance
•
•
•
Next, we shall discuss the problem of finding a
facility location by minimizing the maximum
rectilinear distance from the new facility to all users.
Application: locating emergency facilities.
The procedure is mechanical. First, the procedure
will be discussed. Then, the procedure will be
illustrated with an example.
Minimize Maximum
Rectilinear Distance
• Compute five numbers c1, c2, c3, c4, c5:
c1  min (ai  bi )
1i  n
c2  max (ai  bi )
1i  n
c3  min ( ai  bi )
1i  n
c4  max (ai  bi )
1i  n
c5  max( c2  c1 , c4  c3 )
Minimize Maximum
Rectilinear Distance
• Define:
x1  (c1  c3 ) / 2, y1  (c1  c3  c5 ) / 2
x2  (c2  c4 ) / 2, y2  (c2  c4  c5 ) / 2
• All points along the line connecting (x1,y1) and (x2,y2)
are optimal
Example: Minimize Maximum
Rectilinear Distance
First, compute c1, c2, c3, c4, c5:
Tract
(ai,bi)
A
(2.5,4.5)
B
(3.0,2.5)
D
(5.0,2.0)
C
(5.5,4.0)
E
(8.0,5.0)
Min
Max
c5  max( c2  c1 , c4  c3 ) 
ai+bi
c1 =
c2 =
-ai+bi
c3 =
c4 =
Example: Minimize Maximum
Rectilinear Distance
x1  (c1  c3 ) / 2 
y1  (c1  c3  c5 ) / 2 
x2  (c2  c4 ) / 2 
y2  (c2  c4  c5 ) / 2 
• All points along the line connecting ____________
and ____________ are optimal.
Example: Minimize Maximum
Rectilinear Distance
• Notice that instead of getting one optimal location we
obtained infinite number of optimal locations I.e., any
point along the lines connecting (4.25,5.0) and
(5.5,3.75).
• To get the optimal value, compute the maximum
rectilinear distances from any optimal location, say
(4.25, 5.0). This is done on the next two slides.
Example: Minimize Maximum
Rectilinear Distance
Maximum rectilinea r distance
From optimal location (4.25,5.0)
 max i  4.25  ai  5.0  bi


Example: Minimize Maximum
Rectilinear Distance
Continues from the previous slide
READING AND EXERCISES
Lesson 21
Reading:
– Section 10.8-10.9 pp. 598-606 (4th Ed.), pp. 575-584
(5th Ed.)
Exercises:
– 10.25 p. 600, 10.32, 10.38, pp. 608-609 (4th Ed.)
– 10.25 p. 578, 10.32, 10.38, p. 585 (5th Ed.)
LESSON 22: LOCATING A SINGLE FACILITY
THE EUCLIDEAN DISTANCE PROBLEM
Outline
• Minimize Weighted Sum of the Squares of the
Euclidean Distances (Gravity Problem)
• Minimize Weighted Sum of the Euclidean Distances
The Euclidean Distance Problem
• Lesson 15 discusses the rectilinear distance
problems. In this lesson, we shall discuss Euclidean
distance problems with the following two objectives
– Minimize weighted sum of the squares of the
Euclidean distances a.k.a the gravity problem
(approximation to the other objective)
– Minimize weighted sum of the Euclidean distances
The Euclidean Distance Problem
• Notations:
– X-coordinate of existing facility i = ai
– Y-coordinate of existing facility i = bi
– Weight assigned to user location i = wi
– Location of the proposed facility = (x,y)
– Euclidean distance = ( x  ai ) 2  ( y  bi ) 2
Example
The Euclidean Distance Problem
• The new health-watch facility is targeted to serve five
census tracts in Erie, Pennsylvania. Coordinates for
the center of each census tract, along with the
projected populations, measured in thousands are
shown next. Customers will travel from the five
census tract centers to the new facility when they
need health care.
Example
The Euclidean Distance Problem
Census Tract
A
B
C
D
E
(ai,bi)
(2.5,4.5)
(3.0,2.5)
(5.5,4.0)
(5.0,2.0)
(8.0,5.0)
Population, wi
2
5
10
7
12
Gravity Problem
Minimize Weighted Sum of the Squares of the
Euclidean Distances
• The problem of minimizing weighted sum of the
Euclidean distances is difficult and solved by an
iterative procedure. The initial solution of the iterative
procedure is obtained from the solution of the gravity
problem which minimizes weighted sum of the
squares of the Euclidean distances. The solution of
the gravity problem is obtained using the following
n
n
formula:
wi bi
wi ai


y *  i 1n
x*  i 1n
 wi
 wi
i 1
i 1
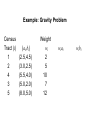
Example: Gravity Problem
Census
Tract (i)
1
2
4
3
5
(ai,bi)
(2.5,4.5)
(3.0,2.5)
(5.5,4.0)
(5.0,2.0)
(8.0,5.0)
Weight
wi
2
5
10
7
12
wiai
wibi
Example: Gravity Problem
n
x* 
wa
i 1
n
i i
w
i 1
i
n

y* 
wb
i 1
n
i i
w
i 1

i
Conclusion: The location ___________________
minimizes the weighted sum of the squares of the
Euclidean distances.
Example: Gravity Problem
Euclidean distance =
( x  ai ) 2  ( y  bi ) 2
Square of the Euclidean distance = ( x  ai ) 2  ( y  bi ) 2
Weighted sum of the squares of the
Euclidean distances from optimal location
(5.72,3.76 ) to 5 locations
5

  wi 5.72  ai   3.76  bi 
i 1

2
2

Example: Gravity Problem
Continues from the previous slide
Minimize Weighted Sum of the Euclidean
Distances
Use the following procedure to find a location that
minimizes weighted sum of the Euclidean distances.
The procedure is iterative, starts with a trial solution
and converges to an optimal solution.
Step 1: Consider a trial location (x,y). The solution to the
gravity problem is a good trial solution.
Step 2: For each location (ai,bi) compute
wi
gi 
( x  ai ) 2  ( y  bi ) 2
Minimize Weighted Sum of the Euclidean
Distances
Step 3: Modify the x and y values as follows:
n
n
x
a g
i 1
n
i
g
i 1
i
i
y
b g
i 1
n
i
g
i 1
i
i
Step 4: If one or both of (x,y) changes, repeat the process
with the modified (x,y). Go to step 2 with modified (x,y). If
none of (x,y) changes, stop.
Note: This procedure is better done by spreadsheet. It’s easy
to set up one.One is also available from the course web site.
Example: Minimize Weighted Sum of the
Euclidean Distances
Step 1: Consider the trial solution (x,y) = (5.72, 3.76) that
is obtained from the gravity problem.
Step 2:
Trial location
xi
yi
ai
5.72
bi
wi
gi
2.5
3
5
5.5
8
4.5
2.5
2
4
5
2
5
7
10
12
0.61
1.67
3.68
30.71
4.62
3.76
Example: Minimize Weighted Sum of the
Euclidean Distances
Sample computation for the previous slide:
w1
w1
g1 

2
2
x  a1    y  b1 
5.72  a1 2  3.76  b1 2

g2 

w2
x  a2    y  b2 
2
2

w2
5.72  a2 2  3.76  b2 2
Example: Minimize Weighted Sum of the
Euclidean Distances
Step 3:
Modified
Trial location
xi
yi
ai
5.72
bi
wi
gi
aigi
bigi
2.5
3
5
5.5
8
4.5
2.5
2
4
5
2
5
7
10
12
0.61
1.67
3.68
30.71
4.62
41.29
1.51
5.00
18.41
168.93
36.99
230.84
2.72
4.17
7.36
122.86
23.12
160.23
3.76
Total
x = (230.84/41.29) = 5.59
y = (160.23/41.29) = 3.88
Example: Minimize Weighted Sum of the
Euclidean Distances
Sample computation for the previous slide:
a1 g1 
a2 g 2 
a g
b g
i
i

i
i

n
n
x
a g
i 1
n
i
g
i 1
i
=
i
y
b g
i 1
n
i
g
i 1
i
=
i
Example: Minimize Weighted Sum of the
Euclidean Distances
• Repeat the process with (x,y) = (5.59, 3.88). The
result is (x,y) = (5.54, 3.94).
• Repeat the process with (x,y) = (5.54, 3.94). The
result is (x,y) = (5.52, 3.97).
• Repeat the process with (x,y) = (5.52, 3.97). The
result is (x,y) = (5.51, 3.98).
• Repeat the process with (x,y) = (5.51, 3.98). The
result is (x,y) = (5.51, 3.99).
• Repeat the process with (x,y) = (5.51, 3.99). The
result is (x,y) = (5.50, 3.99).
• Repeat the process with (x,y) = (5.50, 3.99). The
result is (x,y) = (5.50, 3.99).
• Stop.
Example: Minimize Weighted Sum of the
Euclidean Distances
Euclidean distance =
( x  ai ) 2  ( y  bi ) 2
Weighted sum of the Euclidean distances
from location (5.50,3.99 ) to 5 locations
5
  wi
i 1

5.50  ai 2  3.99  bi 2
Example: Minimize Weighted Sum of the
Euclidean Distances
Continues from the previous slide
Application
1. Minimize weighted sum of the rectilinear distances (done)
– Facilities used by many people e.g., computer centre,
gymnasium
2. Minimize maximum rectilinear distance (done)
– Emergency facilities e.g., police, fire
3. Minimize weighted sum of the Euclidean distances (done)
– Utilities, e.g., phone cable
4. Minimize maximum Euclidean distance (not in book)
– Transmission towers e.g., radio towers
5. Minimize weighted sum of the squares of the Euclidean
distances (done)
– Approximation for 3.
READING AND EXERCISES
Lesson 22
Reading:
– Section 10.10 pp. 609-612 (4th Ed.), pp. 586-588 (5th
Ed.)
Exercises:
– 10.41 p. 612 (4th Ed.) p. 589 (5th Ed.)
LESSON 23/24:
COMPUTERIZED LAYOUT TECHNIQUE
Outline
• Computerized Layout Technique
– A Layout Improvement Procedure, CRAFT
• Distance Between Two Departments
• Total Distance Traveled
• Savings and a Sample Computation
• Improvement Procedure
• Exact Centroids
– A Layout Construction Procedure, ALDEP
Computerized Layout Technique
• Suppose that we are given some space for some
departments. How shall we arrange the departments
within the given space?
• We shall assume that the given space is rectangular
shaped and every department is either rectangular
shaped or composed of rectangular pieces.
• We shall discuss
– a layout improvement procedure, CRAFT, that
attempts to find a better layout by pair-wise
interchanges when a layout is given and
– a layout construction procedure, ALDEP, that
constructs a layout when there is no layout given.
Following are
some
examples of
questions
addressed by
CRAFT:
• Is this a good
layout?
• If not, can it be
improved?
10 20 30 40 50 60 70 80 90 100
CRAFT - Computerized Relative Allocation of
Facilities Technique
A
D
C
B
10 20 30 40 50 60 70 80 90 100
CRAFT: Distance Between Two Departments
• Consider the problem of finding the distance between two
adjacent departments, separated by a line only.
• People needs walking to move from one department to
another, even when the departments are adjacent.
• An estimate of average walking required is obtained from
the distance between centroids of two departments.
• Centroid of a rectangle is the point where two diagonals
meet. So, if a rectangle has two opposite corners x1 , y1 
and x2 , y2  then the centroid is
 x1  x2 y1  y2 
,


2 
 2
• See Slide 7 for an example of finding centroid.
CRAFT: Distance Between Two Departments
• Finding centroid of a shape composed of rectangular
pieces involves more computation and discussed on
Slides 21-25.
• The distance between two departments is taken from the
distance between their centroids.
• People walks along some rectilinear paths. An Euclidean
distance between two centroids is not a true
representative of the walking required. The rectilinear
distance is a better approximation.
• So, Distance (A,B) = rectilinear distance between
centroids of departments A and B
CRAFT: Distance Between Two Departments
• Let
– Centroid of Department A = xA , yA 
– Centroid of Department B = xB , yB 
• Then, the distance between departments A and B,
Dist(A,B)
 xA  xB  y A  yB
• The distance formula is illustrated with an example
on the next slide. The distance between departments
A and C is the rectilinear distance between their
centroids (30,75) and (80,35). Distance (A,C)
 xA  xC  y A  yC  30  80  75  35  90
Centroid of A
=
Centroid of C
=
Distance (A,C)
=
10 20 30 40 50 60 70 80 90 100
CRAFT: Distance Between Two Departments
A
D
(80,85)
C
B
(30,25)
10 20 30 40 50 60 70 80 90 100
CRAFT: Total Distance Traveled
• If the number of trips between two departments are very
high, then such departments should be placed near to
each other in order to minimize the total distance traveled.
• Distance traveled from department A to B = Distance (A,B)
 Number of trips from department A to B
• Total distance traveled is obtained by computing distance
traveled between every pair of departments, and then
summing up the results.
• Given a layout, CRAFT first finds the total distance
traveled.
• The next 3 slides illustrates finding total distance traveled.
To
CRAFT: Total
Distance Traveled
(a) Material handling trips
(given)
From
A
B
C
D
A
3
6
7
B
2
7
7
C
7
5
3
D
4
7
3
(a)
To
CRAFT: Total
Distance Traveled
(a) Material handling trips
(given)
From
A
B
C
D
(b) Distances (given)
3
6
7
To
From
A
B
C
D
A
A
50
90
60
B
2
7
7
B
50
60
110
C
7
5
D
4
7
3
(a)
3
C
90
60
50
D
60
110
50
(b)
To
CRAFT: Total
Distance Traveled
(a) Material handling trips
(given)
From
A
B
C
D
3
6
7
To
From
(b) Distances (given)
(c) Sample computation:
distance traveled (A,B)
= trips (A,B)  dist (A,B)
=
Total distance traveled
= 100+630+240+….
= 4640
A
B
C
D
A
B
C
D
A
50
90
60
To
From
A
A
150
540
420
B
2
7
7
B
50
60
110
B
100
420
770
C
7
5
D
4
7
3
(a)
3
C
90
60
D
60
110
50
(b)
50
C
630
300
150
D
240
770
150
(c)
CRAFT: Savings
• As stated before, given a layout CRAFT first finds the total
distance traveled as illustrated on the previous 3 slides.
CRAFT then attempts to improve the layout by pair-wise
interchanges.
• If some interchange results some savings in the total
distance traveled, the interchange that saves the most
(total distance traveled) is selected.
• While searching for the most savings, exact savings are
not computed. At the search stage, savings are computed
assuming when departments are interchanged, centroids
are interchanged too. This assumption does not give the
exact savings, but approximate savings only.
• Exact centroids are computed later.
CRAFT: Savings
• Savings are computed for all feasible pairwise interchanges.
Savings are not computed for the infeasible interchanges.
• An interchange between two departments is feasible only if
the departments have the same area or they share a
common boundary. For the layout shown on Slide 7:
– feasible pairs are {A,B}, {A,C}, {A,D}, {B,C}, {C,D}
– and an infeasible pair is {B,D}
• For the layout shown on Slide 7, savings are not computed
for interchanging B and D. Savings are computed for each of
the 5 other pair-wise interchanges and the best one chosen.
• After the departments are interchanged, every exact centroid
is found. This may require more computation if one or more
shape is composed of rectangular pieces. See Slides 21-25.
CRAFT: A Sample Computation of Savings
from a Feasible Pairwise Interchange
• To illustrate the computation of savings, we shall compute
the savings from interchanging Departments C and D
• New centroids:
A (30,75)
Unchanged
B (30,25)
Unchanged
C (80,85)
Previous centroid of Department D
D (80,35)
Previous centroid of Department C
• Note: If C and D are interchanged, exact centroids are
C(80,65) and D(80,15). So, the centroids C(80,85) and
D(80,35) are not exact, but approximate.
CRAFT: A Sample Computation of Savings
from a Feasible Pairwise Interchange
• The first job in the computation of savings is to reconstruct
the distance matrix that would result if the interchange was
made.
• The purpose of using approximate centroids will be clearer
now.
• If the exact centroids were used, we would have to
recompute distances between every pair of departments
that would include one or both of C and D.
• However, since we assume that centroids of C and D will
be interchanged, the new distance matrix can be obtained
just by rearranging some rows and columns of the original
distance matrix. This will now be shown.
CRAFT: A Sample Computation of Savings
from a Feasible Pairwise Interchange
• The matrix on the left is the previous matrix, before
interchange (see Slide 7). The matrix on the right is after.
• Dist (A,B) and (C,D) does not change.
• New dist (A,C) = Previous dist (A,D)
Interchange
C,D
• New dist (A,D) = Previous dist (A,C)
• New dist (B,C) = Previous dist (B,D)
• New dist (B,D) = Previous dist (A,C)
To
From
A
B
C
D
A
50
90
60
B
50
60
110
C
90
60
50
D
60
110
50
To
From
A
B
C
D
A
50
60
90
B
50
110
60
C
60
110
50
D
90
60
50
CRAFT: A Sample
Computation of
Savings
(a) Material handling trips
(given)
To
From
A
B
C
D
A
3
6
7
B
2
7
7
C
7
5
3
D
4
7
3
(a)
CRAFT: A Sample
Computation of
Savings
(a) Material handling trips
(given)
(b) Distances (rearranged)
To
From
A
B
C
D
3
6
7
To
From
A
B
C
D
A
A
50
60
90
B
2
7
7
B
50
110
60
C
7
5
D
4
7
3
(a)
3
C
60
110
50
D
90
60
50
(b)
CRAFT: A Sample
Computation of
Savings
(a) Material handling trips
(given)
(b) Distances (rearranged)
(c) Sample computation:
distance traveled (A,B)
= trips (A,B)  dist (A,B)
=
Total distance traveled
= 100+420+360+…
= 4480
Savings
=
To
From
A
B
C
D
3
6
7
To
From
A
B
C
D
A
B
C
D
A
50
60
90
To
From
A
A
150
360
630
B
2
7
7
B
50
110
60
B
100
770
420
C
7
5
D
4
7
3
(a)
3
C
60
110
D
90
60
50
(b)
50
C
420
550
150
D
360
420
150
(c)
CRAFT: Improvement Procedure
• To complete the exercise
1. Compute savings from all the feasible interchanges.
If there is no (positive) savings, stop.
2. If any interchange gives some (positive) savings,
choose the interchange that gives the maximum
savings
3. If an interchange is chosen, then for every
department find an exact centroid after the
interchange is implemented
4. Repeat the above 3 steps as longs as Step 1 finds
an interchange with some (positive) savings.
• Sometimes, an interchange may
result in a peculiar shape of a
department; a shape that is
composed of some rectangular
pieces
• For example, consider the layout
on Slide 7 and interchange
departments A and D. The
resulting picture is shown on the
right.
• How to compute the exact
coordinate of the centroid (of a
shape like A)?
10 20 30 40 50 60 70 80 90 100
CRAFT: Exact Coordinates of Centroids
D
A
C
B
10 20 30 40 50 60 70 80 90 100
Let
A1  Area A1 
A2  Area A2 
x1 , y1 
 Centroid of A1

x2 , y2 
 Centroid of A1

50 60 70 80 90 100
CRAFT: Exact Coordinates of Centroids
A
A1
A2
10 20 30 40 50 60 70 80 90 100
Find the centroid of A
CRAFT: Exact Coordinates of Centroids
Rectangle
(1)
A1
A2
Total
Area
(2)
X-coordinate Multiply
of centroid (2) and (3)
(3)
(4)
X-coordinate of the centroid of A 

A1 x1  A2 x2
A1  A2
CRAFT: Exact Coordinates of Centroids
Rectangle
(1)
A1
A2
Total
Area
(2)
Y-coordinate Multiply
of centroid (2) and (3)
(3)
(4)
Y-coordinate of the centroid of A 

A1 y1  A2 y2
A1  A2
50 60 70 80 90 100
CRAFT: Exact Coordinates of Centroids
A
A1
A2
10 20 30 40 50 60 70 80 90 100
Exact coordinate of area A is
CRAFT: Some Comments
• An improvement procedure, not a construction procedure
• At every stage some pairwise interchanges are
considered and the best one is chosen
• Interchanges are only feasible if departments have the
same area; or they share a common boundary
• Departments of unequal size that are not adjacent are
not considered for interchange
• Estimated cost reduction may not be obtained after
interchange (because the savings are based on
approximate centroids)
• Strangely shaped departments may be formed
ALDEP
Automated Layout Design Program
• While CRAFT is an improvement procedure, ALDEP is
a construction procedure.
• CRAFT requires an initial layout, which is improved by
CRAFT. ALDEP does not need any initial layout. ALDEP
constructs a layout when there is none.
• Previously, in Lesson 13, we have discussed a
construction procedure and an improvement procedure
in the context of vehicle scheduling. The nearest
neighbor heuristic is a tour construction procedure
which may be improved by eliminating intersections.
ALDEP
• Given
– Size of the facility
– The departments
– Size of the departments
– Proximity relationships (activity relationship chart) and
– A sweep width (defined later)
ALDEP constructs a layout.
ALDEP
• The size of the facility and the size of the departments are
expressed in terms of blocks.
• The procedure will be explained with an example. Suppose
that the facility is 8 blocks (horizontal)  6 block (vertical).
• The departments and the required number of blocks are:
– Production area
14 blocks
– Office rooms
10
– Storage area
8
– Dock area
8
– Locker room
4
– Tool room
4
ALDEP
A: absolutely necessary
E: especially important
I: important
O: ordinarily important
U: unimportant
X: undesirable Production area
Office rooms
O
A
U
I
O
Storage
A
Dock area
X
U
U
U
U
O
O
Locker room
Tool room
E
A
ALDEP
• The proximity relationships are shown on the previous
slide.
• ALDEP starts to allocate the departments from the upper
left corner of the facility. The first department is chosen at
random. By starting with a different department, ALDEP
can find a different layout for the same problem.
• Let’s start with dock rooms (D). On
D D
the upper left corner 8 blocks must
D D
be allocated for the dock area.
D D
• The sweep width defines the width
D D
in number of blocks. Let sweep
width = 2. Then, dock area will be
allocated 2  4 = 8 blocks.
ALDEP
• To find the next department to allocate, find the
department that has the highest proximity rating with the
dock area as given on Slide 30. Storage area (S) has the
highest proximity rating A with the dock area.
• So, the storage area will be allocated next. The storage
area also needs 8 blocks.
• There are only 2 2 = 4 blocks,
D D
remaining below dock area (D).
After allocating 4 blocks, the down D D
D D
wall is hit after which further
D D
allocation will be made on the
S S S S
adjacent 2 (=sweep width)
S S S S
columns and moving upwards.
ALDEP
• See carefully that the allocation started from the upper left
corner and started to move downward with an width of 2
(=sweep width) blocks.
• After the down wall is hit, the allocation continues on the
adjacent 2 (=sweep width) columns on the right side and
starts moving up.
• This zig-zag pattern will continue.
D D
• Next time, when the top wall will
D D
be hit, the allocation will continue
D D
on the adjacent 2 (=sweep width)
D D
columns on the right side and
S S S S
starts moving down.
S S S S
ALDEP
• To find the next department to allocate, find the
department that has the highest proximity rating with
storage area as given on Slide 30.
• Production area (P) has the highest proximity rating A with
the storage area.
• The production area needs 14 blocks.
• After allocating 8 blocks, the top
D D P P P P
wall is hit and the remaining 6
D D P P P P
blocks are allocated on the
D D P P P P
adjacent 2 (=sweep width)
columns moving downward.
D D P P
S S S S
S S S S
ALDEP
• To find the next department to allocate, find the
department that has the highest proximity rating with
production area as given on Slide 30.
• Tool room (T) has the highest proximity rating A with the
production area.
• The tool room needs 4 blocks. So, 4 blocks are allocated.
• Next, there is a tie. See from Slide
D D P P P P
30 that both locker room (L) and
office room (O) have the proximity D D P P P P
D D P P P P
rating of U with the tool room.
D D P P T T
• Ties are broken at random. So,
any of the locker room or the office S S S S T T
room can be allocated next.
S S S S
ALDEP
• Let’s choose locker room (L) room at random. Then, the
last department must be office room (O). The resulting
layout is shown below.
• Note that since the ALDEP chooses the first department
at random and since the ties are broken at random,
ALDEP can give many solutions to the same problem.
• Using the layout, the adjacency
relationships and the proximity
ratings, we can find an overall
rating of each layout. Then, the
layout with the highest overall
rating is selected. This will now be
discussed.
D
D
D
D
S
S
D
D
D
D
S
S
P
P
P
P
S
S
P
P
P
P
S
S
P
P
P
T
T
L
P
P
P
T
T
L
O
O
O
O
O
L
O
O
O
O
O
L
ALDEP
• After a layout is obtained, a score for the layout is
computed with the following conversion of proximity
relationships:
A = 43
= 64,
E
= 42 = 16
I = 41 = 4,
O
= 40 = 1
U = 0,
X
= -45 = -1024
• If two departments are adjacent in the layout then the
weight corresponding to the rating between the two
departments is added to the score.
ALDEP
• Let’s compute the overall rating of the layout constructed.
To do this, we shall list every pair of adjacent
departments. For each pair, a letter rating will be obtained
from the activity relationship chart (a.k.a. rel chart) on
Slide 30 and then the score will be converted to a numeric
score using the conversion scheme on the previous slide.
• Adjacent departments:
(D,S)
(D,P)
(S,P)
(S,T)
(S,L)
(P,T)
(P,O)
(T,L)
(T,O)
(L,O)
D
D
D
D
S
S
D
D
D
D
S
S
P
P
P
P
S
S
P
P
P
P
S
S
P
P
P
T
T
L
P
P
P
T
T
L
O
O
O
O
O
L
O
O
O
O
O
L
ALDEP
Adjacent
Departments
(D,S)
(D,P)
(S,P)
(S,T)
(S,L)
(P,T)
(P,O)
(T,L)
(T,O)
(L,O)
Proximity
Ratings (Slide 30)
A
I
A
O
U
A
O
U
U
X
Numeric
Scores (Slide 37)
43=64
41=4
43=64
40=1
0
43=64
40=64
0
0
-45= -1024
Total = -763
ALDEP
• The process is repeated several times and the layout
with the highest score is chosen.
• Notice the large negative weight associated with X
ratings.
• If the departments which cannot be next to each other,
are adjacent in a layout, then the layout score reduces
significantly.
• This is important because ALDEP also uses a cut-off
score (if not specified by the user this cut-off is zero) to
eliminate any layout which has a layout score less than
the cut-off score.
READING AND EXERCISES
Lesson 23/24
Reading:
– Section 10.6 pp. 575-581 (CRAFT), 581-582 (ALDEP)
(4th Ed.), pp. 555-559 (CRAFT), 560-561 (ALDEP) (5th
Ed.)
– Appendix 10-A pp. 626-628 (4th Ed.), pp. 602-604 (5th
Ed.)
Exercises:
– 10.13, 10.15, 10.19, pp. 586-587 (4th Ed.), pp. 564567 (5th Ed.)