* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download lecture13_densela_1_.. - People @ EECS at UC Berkeley
Jordan normal form wikipedia , lookup
Determinant wikipedia , lookup
System of linear equations wikipedia , lookup
Four-vector wikipedia , lookup
Eigenvalues and eigenvectors wikipedia , lookup
Matrix (mathematics) wikipedia , lookup
Cayley–Hamilton theorem wikipedia , lookup
Matrix calculus wikipedia , lookup
Symmetric cone wikipedia , lookup
Non-negative matrix factorization wikipedia , lookup
Singular-value decomposition wikipedia , lookup
Perron–Frobenius theorem wikipedia , lookup
Gaussian elimination wikipedia , lookup
CS 267
Dense Linear Algebra:
History and Structure,
Parallel Matrix Multiplication
James Demmel
www.cs.berkeley.edu/~demmel/cs267_Spr10
3/02/2010
CS267 Lecture 13
1
Outline
•
•
•
•
History and motivation
Structure of the Dense Linear Algebra motif
Parallel Matrix-matrix multiplication
Parallel Gaussian Elimination (next time)
3/02/2010
CS267 Lecture 13
2
Outline
•
•
•
•
History and motivation
Structure of the Dense Linear Algebra motif
Parallel Matrix-matrix multiplication
Parallel Gaussian Elimination (next time)
3/02/2010
CS267 Lecture 13
3
Motifs
The Motifs (formerly “Dwarfs”) from
“The Berkeley View” (Asanovic et al.)
Motifs form key computational patterns
4
A brief history of (Dense) Linear Algebra software (1/6)
• In the beginning was the do-loop…
• Libraries like EISPACK (for eigenvalue problems)
• Then the BLAS (1) were invented (1973-1977)
• Standard library of 15 operations (mostly) on vectors
• “AXPY” ( y = α·x + y ), dot product, scale (x = α·x ), etc
• Up to 4 versions of each (S/D/C/Z), 46 routines, 3300 LOC
• Goals
• Common “pattern” to ease programming, readability, selfdocumentation
• Robustness, via careful coding (avoiding over/underflow)
• Portability + Efficiency via machine specific implementations
• Why BLAS 1 ? They do O(n1) ops on O(n1) data
• Used in libraries like LINPACK (for linear systems)
• Source of the name “LINPACK Benchmark” (not the code!)
3/02/2010
CS267 Lecture 13
5
Current Records for Solving Dense Systems (11/2009)
www.top500.org,
Machine
www.netlib.org/performance
Gigaflops
n=100 n=1000 Any n
“Jaguar” (ORNL)
1.76M
(1.76 Petaflops, 224K cores, 7 MW, n=5.5M)
NEC SX 8 (data from 2005)
(8 proc, 2 GHz)
(1 proc, 2 GHz)
2.2
75.1
15.0
Peak
2.3M
128
16
…
Palm Pilot III
3/02/2010
.00000169
(1.69 Kiloflops)
CS267 Lecture 13
6
A brief history of (Dense) Linear Algebra software (2/6)
• But the BLAS-1 weren’t enough
• Consider AXPY ( y = α·x + y ): 2n flops on 3n read/writes
• Computational intensity = (2n)/(3n) = 2/3
• Too low to run near peak speed (read/write dominates)
• Hard to vectorize (“SIMD’ize”) on supercomputers of the
day (1980s)
• So the BLAS-2 were invented (1984-1986)
• Standard library of 25 operations (mostly) on
matrix/vector pairs
• “GEMV”: y = α·A·x + β·x, “GER”: A = A + α·x·yT, x = T-1·x
• Up to 4 versions of each (S/D/C/Z), 66 routines, 18K LOC
• Why BLAS 2 ? They do O(n2) ops on O(n2) data
• So computational intensity still just ~(2n2)/(n2) = 2
• OK for vector machines, but not for machine with caches
3/02/2010
CS267 Lecture 13
7
A brief history of (Dense) Linear Algebra software (3/6)
• The next step: BLAS-3 (1987-1988)
• Standard library of 9 operations (mostly) on matrix/matrix
pairs
• “GEMM”: C = α·A·B + β·C, C = α·A·AT + β·C, B = T-1·B
• Up to 4 versions of each (S/D/C/Z), 30 routines, 10K LOC
• Why BLAS 3 ? They do O(n3) ops on O(n2) data
• So computational intensity (2n3)/(4n2) = n/2 – big at last!
• Good for machines with caches, other mem. hierarchy levels
• How much BLAS1/2/3 code so far (all at www.netlib.org/blas)
• Source: 142 routines, 31K LOC, Testing: 28K LOC
• Reference (unoptimized) implementation only
• Ex: 3 nested loops for GEMM
• Lots more optimized code (eg Homework 1)
• Motivates “automatic tuning” of the BLAS (details later)
3/02/2010
CS267 Lecture 13
8
02/25/2009
CS267 Lecture 8
9
A brief history of (Dense) Linear Algebra software (4/6)
• LAPACK – “Linear Algebra PACKage” - uses BLAS-3 (1989 – now)
• Ex: Obvious way to express Gaussian Elimination (GE) is adding
multiples of one row to other rows – BLAS-1
•
How do we reorganize GE to use BLAS-3 ? (details later)
• Contents of LAPACK (summary)
•
•
•
•
•
Algorithms we can turn into (nearly) 100% BLAS 3
– Linear Systems: solve Ax=b for x
– Least Squares: choose x to minimize ||r||2 S ri2 where r=Ax-b
Algorithms that are only 50% BLAS 3 (so far)
– “Eigenproblems”: Find l and x where Ax = l x
– Singular Value Decomposition (SVD): (ATA)x=2x
Generalized problems (eg Ax = l Bx)
Error bounds for everything
Lots of variants depending on A’s structure (banded, A=AT, etc)
• How much code? (Release 3.2, Nov 2008) (www.netlib.org/lapack)
•
Source: 1582 routines, 490K LOC, Testing: 352K LOC
• Ongoing development (at UCB and elsewhere) (class projects!)
3/02/2010
CS267 Lecture 13
10
A brief history of (Dense) Linear Algebra software (5/6)
• Is LAPACK parallel?
• Only if the BLAS are parallel (possible in shared memory)
• ScaLAPACK – “Scalable LAPACK” (1995 – now)
• For distributed memory – uses MPI
• More complex data structures, algorithms than LAPACK
• Only (small) subset of LAPACK’s functionality available
• Details later (class projects!)
• All at www.netlib.org/scalapack
3/02/2010
CS267 Lecture 13
11
Success Stories for Sca/LAPACK (6/6)
• Widely used
• Adopted by Mathworks, Cray,
Fujitsu, HP, IBM, IMSL, Intel,
NAG, NEC, SGI, …
• 5.5M webhits/year @ Netlib
(incl. CLAPACK, LAPACK95)
• New Science discovered through the
solution of dense matrix systems
• Nature article on the flat
universe used ScaLAPACK
• Other articles in Physics
Review B that also use it
• 1998 Gordon Bell Prize
• www.nersc.gov/news/reports/
newNERSCresults050703.pdf
3/02/2010
Cosmic Microwave Background
Analysis, BOOMERanG
collaboration, MADCAP code (Apr.
27, 2000).
CS267 Lecture 13
ScaLAPACK
12
Back to basics:
Why avoiding communication is important (1/2)
Algorithms have two costs:
1.Arithmetic (FLOPS)
2.Communication: moving data between
• levels of a memory hierarchy (sequential case)
• processors over a network (parallel case).
CPU
Cache
CPU
DRAM
CPU
DRAM
CPU
DRAM
CPU
DRAM
DRAM
3/02/2010
CS267 Lecture 13
13
Why avoiding communication is important (2/2)
• Running time of an algorithm is sum of 3 terms:
• # flops * time_per_flop
• # words moved / bandwidth
communication
• # messages * latency
• Time_per_flop << 1/ bandwidth << latency
• Gaps growing exponentially with time
Annual improvements
Time_per_flop
59%
Bandwidth
Latency
Network
26%
15%
DRAM
23%
5%
• Goal : organize linear algebra to avoid communication
• Between all memory hierarchy levels
• L1
L2
DRAM
network, etc
• Not just hiding communication (overlap with arith) (speedup 2x )
• Arbitrary speedups possible
14
3/02/2010
Review: Naïve Sequential MatMul: C = C + A*B
for i = 1 to n
{read row i of A into fast memory, n2 reads}
for j = 1 to n
{read C(i,j) into fast memory, n2 reads}
{read column j of B into fast memory, n3 reads}
for k = 1 to n
C(i,j) = C(i,j) + A(i,k) * B(k,j)
{write C(i,j) back to slow memory, n2 writes}
n3 + O(n2) reads/writes altogether
C(i,j)
=
3/02/2010
A(i,:)
C(i,j)
+
CS267 Lecture 13
*
B(:,j)
15
Less Communication with Blocked Matrix Multiply
• Blocked Matmul C = A·B explicitly refers to subblocks of
A, B and C of dimensions that depend on cache size
… Break Anxn, Bnxn, Cnxn into bxb blocks labeled A(i,j), etc
… b chosen so 3 bxb blocks fit in cache
for i = 1 to n/b, for j=1 to n/b, for k=1 to n/b
C(i,j) = C(i,j) + A(i,k)·B(k,j)
… b x b matmul, 4b2 reads/writes
• (n/b)3 · 4b2 = 4n3/b reads/writes altogether
• Minimized when 3b2 = cache size = M, yielding O(n3/M1/2) reads/writes
• What if we had more levels of memory? (L1, L2, cache etc)?
• Would need 3 more nested loops per level
3/02/2010
CS267 Lecture 13
16
Blocked vs Cache-Oblivious Algorithms
• Blocked Matmul C = A·B explicitly refers to subblocks of
A, B and C of dimensions that depend on cache size
… Break Anxn, Bnxn, Cnxn into bxb blocks labeled A(i,j), etc
… b chosen so 3 bxb blocks fit in cache
for i = 1 to n/b, for j=1 to n/b, for k=1 to n/b
C(i,j) = C(i,j) + A(i,k)·B(k,j)
… b x b matmul
… another level of memory would need 3 more loops
• Cache-oblivious Matmul C = A·B is independent of cache
Function C = RMM(A,B) … R for recursive
If A and B are 1x1
C=A·B
else … Break Anxn, Bnxn, Cnxn into (n/2)x(n/2) blocks labeled A(i,j), etc
for i = 1 to 2, for j = 1 to 2, for k = 1 to 2
C(i,j) = C(i,j) + RMM( A(i,k), B(k,j) )
… n/2 x n/2 matmul
3/02/2010
CS267 Lecture 13
17
Communication Lower Bounds:
Prior Work on Matmul
• Assume n3 algorithm (i.e. not Strassen-like)
• Sequential case, with fast memory of size M
• Lower bound on #words moved to/from slow memory =
(n3 / M1/2 ) [Hong, Kung, 81]
• Attained using blocked or cache-oblivious algorithms
• Parallel case on P processors:
• Let NNZ be total memory needed; assume load balanced
• Lower bound on #words communicated
= (n3 /(P· NNZ )1/2 )
[Irony, Tiskin, Toledo, 04]
NNZ (name of alg) Lower bound
on #words
(“2D alg”)
(n2 / P1/2 )
[Cannon, 69]
3n2 P1/3 (“3D alg”)
(n2 / P2/3 )
[Johnson,93]
3n2
3/02/2010
Attained by
18
New lower bound for all “direct” linear algebra
Let M = “fast” memory size per processor
= cache size (sequential case) or n2/p (parallel case)
#words_moved by at least one processor = (#flops / M1/2 )
#messages_sent by at least one processor = (#flops / M3/2 )
• Holds for
• BLAS, LU, QR, eig, SVD, …
• Some whole programs (sequences of these operations, no
matter how they are interleaved, eg computing Ak)
• Dense and sparse matrices (where #flops << n3 )
• Sequential and parallel algorithms
• Some graph-theoretic algorithms (eg Floyd-Warshall)
• See (partial) proof sketch from Lecture 2
3/02/2010
CS267 Lecture 13
19
Can we attain these lower bounds?
• Do conventional dense algorithms as implemented in
ScaLAPACK attain these bounds?
• Mostly not
• If not, are there other algorithms that do?
• Yes
• Goals for algorithms:
• Minimize #words = (#flops/ M1/2 )
• Minimize #messages = (#flops/ M3/2 )
•
LAPACK and
Need new data structures
• Minimize for multiple memory hierarchy levels
•
Cache-oblivious algorithms would be simplest
• Fewest flops when matrix fits in fastest memory
•
Cache-oblivious algorithms don’t always attain this
• Attainable for nearly all dense linear algebra
• Just a few prototype implementations so far (class projects!)
• Only a few sparse algorithms so far (eg Cholesky)
3/02/2010
CS267 Lecture 13
20
A brief future look at (Dense) Linear Algebra software
• PLASMA and MAGMA (now)
• Planned extensions to Multicore/GPU/Heterogeneous
• Can one software infrastructure accommodate all
algorithms and platforms of current (future) interest?
• How much code generation and tuning can we automate?
• Details later (Class projects!)
• Other related projects
• BLAST Forum (www.netlib.org/blas/blast-forum)
• Attempt to extend BLAS to other languages, add some new
functions, sparse matrices, extra-precision, interval arithmetic
• Only partly successful (extra-precise BLAS used in latest LAPACK)
• FLAME (www.cs.utexas.edu/users/flame/)
• Formal Linear Algebra Method Environment
• Attempt to automate code generation across multiple platforms
3/02/2010
CS267 Lecture 13
21
Outline
•
•
•
•
History and motivation
Structure of the Dense Linear Algebra motif
Parallel Matrix-matrix multiplication
Parallel Gaussian Elimination (next time)
3/02/2010
CS267 Lecture 13
22
What could go into the linear algebra motif(s)?
For all linear algebra problems
For all matrix/problem structures
For all data types
For all architectures and networks
For all programming interfaces
Produce best algorithm(s) w.r.t.
performance and accuracy
(including error bounds, etc)
Need to prioritize, automate!
3/02/2010
CS267 Lecture 13
23
For all linear algebra problems:
Ex: LAPACK Table of Contents
• Linear Systems
• Least Squares
• Overdetermined, underdetermined
• Unconstrained, constrained, weighted
• Eigenvalues and vectors of Symmetric Matrices
•
Standard (Ax = λx), Generalized (Ax=λxB)
• Eigenvalues and vectors of Unsymmetric matrices
•
•
Eigenvalues, Schur form, eigenvectors, invariant subspaces
Standard, Generalized
• Singular Values and vectors (SVD)
• Standard, Generalized
• Level of detail
• Simple Driver
• Expert Drivers with error bounds, extra-precision, other options
• Lower level routines (“apply certain kind of orthogonal transformation”)
3/02/2010
CS267 Lecture 13
24
For all matrix/problem structures:
Ex: LAPACK Table of Contents
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
BD – bidiagonal
GB – general banded
GE – general
GG – general , pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
3/02/2010
•
•
•
•
•
•
•
•
•
•
•
•
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
CS267 Lecture 13
25
For all matrix/problem structures:
Ex: LAPACK Table of Contents
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
BD – bidiagonal
GB – general banded
GE – general
GG – general , pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
3/02/2010
•
•
•
•
•
•
•
•
•
•
•
•
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
CS267 Lecture 13
26
For all matrix/problem structures:
Ex: LAPACK Table of Contents
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
BD – bidiagonal
GB – general banded
GE – general
GG – general, pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
3/02/2010
•
•
•
•
•
•
•
•
•
•
•
•
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
CS267 Lecture 13
27
For all matrix/problem structures:
Ex: LAPACK Table of Contents
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
BD – bidiagonal
GB – general banded
GE – general
GG – general, pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
3/02/2010
•
•
•
•
•
•
•
•
•
•
•
•
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
CS267 Lecture 13
28
For all matrix/problem structures:
Ex: LAPACK Table of Contents
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
BD – bidiagonal
GB – general banded
GE – general
GG – general, pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
3/02/2010
•
•
•
•
•
•
•
•
•
•
•
•
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
CS267 Lecture 13
29
For all matrix/problem structures:
Ex: LAPACK Table of Contents
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
BD – bidiagonal
GB – general banded
GE – general
GG – general, pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
3/02/2010
•
•
•
•
•
•
•
•
•
•
•
•
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
CS267 Lecture 13
30
For all matrix/problem structures:
Ex: LAPACK Table of Contents
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
BD – bidiagonal
GB – general banded
GE – general
GG – general , pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
3/02/2010
•
•
•
•
•
•
•
•
•
•
•
•
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
CS267 Lecture 13
31
For all matrix/problem structures:
Ex: LAPACK Table of Contents
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
BD – bidiagonal
GB – general banded
GE – general
GG – general, pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
3/02/2010
•
•
•
•
•
•
•
•
•
•
•
•
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
CS267 Lecture 13
32
Organizing Linear Algebra – in books
www.netlib.org/lapack
www.netlib.org/scalapack
gams.nist.gov
www.netlib.org/templates
www.cs.utk.edu/~dongarra/etemplates
Outline
•
•
•
•
History and motivation
Structure of the Dense Linear Algebra motif
Parallel Matrix-matrix multiplication
Parallel Gaussian Elimination (next time)
3/02/2010
CS267 Lecture 13
34
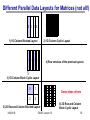
Different Parallel Data Layouts for Matrices (not all!)
0123012301230123
0 1 2 3
1) 1D Column Blocked Layout
2) 1D Column Cyclic Layout
0 1 2 3 0 1 2 3
4) Row versions of the previous layouts
b
3) 1D Column Block Cyclic Layout
0
1
2
3
0
2
0
2
0
2
0
2
1
3
1
3
1
3
1
3
0
2
0
2
0
2
0
2
1
3
1
3
1
3
1
3
0
2
0
2
0
2
0
2
1
3
1
3
1
3
1
3
5) 2D Row and Column Blocked Layout
3/02/2010
CS267 Lecture 13
0
2
0
2
0
2
0
2
1
3
1
3
1
3
1
3
Generalizes others
6) 2D Row and Column
Block Cyclic Layout
35
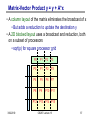
Parallel Matrix-Vector Product
• Compute y = y + A*x, where A is a dense matrix
• Layout:
• 1D row blocked
• A(i) refers to the n by n/p block row
that processor i owns,
• x(i) and y(i) similarly refer to
segments of x,y owned by i
y
• Algorithm:
• Foreach processor i
• Broadcast x(i)
• Compute y(i) = A(i)*x
P0 P1
P2
P3
x
A(0)
P0
A(1)
P1
A(2)
P2
A(3)
P3
• Algorithm uses the formula
y(i) = y(i) + A(i)*x = y(i) + Sj A(i,j)*x(j)
3/02/2010
CS267 Lecture 13
36
Matrix-Vector Product y = y + A*x
• A column layout of the matrix eliminates the broadcast of x
• But adds a reduction to update the destination y
• A 2D blocked layout uses a broadcast and reduction, both
on a subset of processors
• sqrt(p) for square processor grid
3/02/2010
P0
P1
P2
P3
P0
P1
P2
P3
P4
P5
P6
P7
P8
P9
P10 P11
P12
P13 P14 P15
CS267 Lecture 13
37
Parallel Matrix Multiply
• Computing C=C+A*B
• Using basic algorithm: 2*n3 Flops
• Variables are:
• Data layout
• Topology of machine
• Scheduling communication
• Use of performance models for algorithm design
• Message Time = “latency” + #words * time-per-word
= a + n*b
• Efficiency (in any model):
• serial time / (p * parallel time)
• perfect (linear) speedup efficiency = 1
3/02/2010
CS267 Lecture 13
38
Matrix Multiply with 1D Column Layout
• Assume matrices are n x n and n is divisible by p
p0 p1 p2 p3 p4 p5 p6 p7
May be a reasonable
assumption for analysis,
not for code
• A(i) refers to the n by n/p block column that processor i
owns (similiarly for B(i) and C(i))
• B(i,j) is the n/p by n/p sublock of B(i)
• in rows j*n/p through (j+1)*n/p - 1
• Algorithm uses the formula
C(i) = C(i) + A*B(i) = C(i) + Sj A(j)*B(j,i)
3/02/2010
CS267 Lecture 13
39
Matrix Multiply: 1D Layout on Bus or Ring
• Algorithm uses the formula
C(i) = C(i) + A*B(i) = C(i) + Sj A(j)*B(j,i)
• First consider a bus-connected machine without
broadcast: only one pair of processors can
communicate at a time (ethernet)
• Second consider a machine with processors on a ring:
all processors may communicate with nearest neighbors
simultaneously
3/02/2010
CS267 Lecture 13
40
MatMul: 1D layout on Bus without Broadcast
Naïve algorithm:
C(myproc) = C(myproc) + A(myproc)*B(myproc,myproc)
for i = 0 to p-1
for j = 0 to p-1 except i
if (myproc == i) send A(i) to processor j
if (myproc == j)
receive A(i) from processor i
C(myproc) = C(myproc) + A(i)*B(i,myproc)
barrier
Cost of inner loop:
computation: 2*n*(n/p)2 = 2*n3/p2
communication: a + b*n2 /p
3/02/2010
CS267 Lecture 13
41
Naïve MatMul (continued)
Cost of inner loop:
computation: 2*n*(n/p)2 = 2*n3/p2
communication: a + b*n2 /p
… approximately
Only 1 pair of processors (i and j) are active on any iteration,
and of those, only i is doing computation
=> the algorithm is almost entirely serial
Running time:
= (p*(p-1) + 1)*computation + p*(p-1)*communication
2*n3 + p2*a + p*n2*b
This is worse than the serial time and grows with p.
When might you still want to do this?
3/02/2010
CS267 Lecture 13
42
Matmul for 1D layout on a Processor Ring
• Pairs of adjacent processors can communicate simultaneously
Copy A(myproc) into Tmp
C(myproc) = C(myproc) + Tmp*B(myproc , myproc)
for j = 1 to p-1
Send Tmp to processor myproc+1 mod p
Receive Tmp from processor myproc-1 mod p
C(myproc) = C(myproc) + Tmp*B( myproc-j mod p , myproc)
• Same idea as for gravity in simple sharks and fish algorithm
• May want double buffering in practice for overlap
• Ignoring deadlock details in code
• Time of inner loop = 2*(a + b*n2/p) + 2*n*(n/p)2
3/02/2010
CS267 Lecture 13
43
Matmul for 1D layout on a Processor Ring
• Time of inner loop = 2*(a + b*n2/p) + 2*n*(n/p)2
• Total Time = 2*n* (n/p)2 + (p-1) * Time of inner loop
•
2*n3/p + 2*p*a + 2*b*n2
• (Nearly) Optimal for 1D layout on Ring or Bus, even with Broadcast:
• Perfect speedup for arithmetic
• A(myproc) must move to each other processor, costs at least
(p-1)*cost of sending n*(n/p) words
• Parallel Efficiency = 2*n3 / (p * Total Time)
= 1/(1 + a * p2/(2*n3) + b * p/(2*n) )
= 1/ (1 + O(p/n))
• Grows to 1 as n/p increases (or a and b shrink)
3/02/2010
CS267 Lecture 13
44
MatMul with 2D Layout
• Consider processors in 2D grid (physical or logical)
• Processors can communicate with 4 nearest neighbors
• Broadcast along rows and columns
p(0,0)
p(0,1)
p(0,2)
p(1,0)
p(1,1)
p(1,2)
p(2,0)
p(2,1)
p(2,2)
=
p(0,0)
p(0,1)
p(0,2)
p(1,0)
p(1,1)
p(1,2)
p(2,0)
p(2,1)
p(2,2)
*
p(0,0)
p(0,1)
p(0,2)
p(1,0)
p(1,1)
p(1,2)
p(2,0)
p(2,1)
p(2,2)
• Assume p processors form square s x s grid, s = p1/2
3/02/2010
CS267 Lecture 13
45
Cannon’s Algorithm
… C(i,j) = C(i,j) + Sk A(i,k)*B(k,j)
… assume s = sqrt(p) is an integer
forall i=0 to s-1
… “skew” A
left-circular-shift row i of A by i
… so that A(i,j) overwritten by A(i,(j+i)mod s)
forall i=0 to s-1
… “skew” B
up-circular-shift column i of B by i
… so that B(i,j) overwritten by B((i+j)mod s), j)
for k=0 to s-1
… sequential
forall i=0 to s-1 and j=0 to s-1 … all processors in parallel
C(i,j) = C(i,j) + A(i,j)*B(i,j)
left-circular-shift each row of A by 1
up-circular-shift each column of B by 1
3/02/2010
CS267 Lecture 13
46
Cannon’s Matrix Multiplication
C(1,2) = A(1,0) * B(0,2) + A(1,1) * B(1,2) + A(1,2) * B(2,2)
3/02/2010
CS267 Lecture 13
47
Initial Step to Skew Matrices in Cannon
• Initial blocked input
A(0,0) A(0,1) A(0,2)
B(0,0) B(0,1) B(0,2)
A(1,0) A(1,1) A(1,2)
B(1,0) B(1,1) B(1,2)
A(2,0) A(2,1) A(2,2)
B(2,0) B(2,1) B(2,2)
• After skewing before initial block multiplies
A(0,0) A(0,1) A(0,2)
B(0,0) B(1,1) B(2,2)
A(1,1) A(1,2) A(1,0)
B(1,0) B(2,1) B(0,2)
A(2,2) A(2,0) A(2,1)
B(2,0) B(0,1) B(1,2)
3/02/2010
CS267 Lecture 13
48
Skewing Steps in Cannon
All blocks of A must multiply all like-colored blocks of B
• First step
• Second
• Third
3/02/2010
A(0,0) A(0,1) A(0,2)
B(0,0) B(1,1) B(2,2)
A(1,1) A(1,2) A(1,0)
B(1,0) B(2,1) B(0,2)
A(2,2) A(2,0) A(2,1)
B(2,0) B(0,1) B(1,2)
A(0,1) A(0,2) A(0,0)
B(1,0) B(2,1) B(0,2)
A(1,2) A(1,0) A(1,1)
B(2,0) B(0,1) B(1,2)
A(2,0) A(2,1) A(2,2)
B(0,0) B(1,1) B(2,2)
A(0,2) A(0,0) A(0,1)
B(2,0) B(0,1) B(1,2)
A(1,0) A(1,1) A(1,2)
B(0,0) B(1,1) B(2,2)
A(2,1) A(2,2) A(2,0)
B(1,0) B(2,1) B(0,2)
CS267 Lecture 13
49
Cost of Cannon’s Algorithm
forall i=0 to s-1
… recall s = sqrt(p)
left-circular-shift row i of A by i … cost ≤ s*(a + b*n2/p)
forall i=0 to s-1
up-circular-shift column i of B by i … cost ≤ s*(a + b*n2/p)
for k=0 to s-1
forall i=0 to s-1 and j=0 to s-1
C(i,j) = C(i,j) + A(i,j)*B(i,j) … cost = 2*(n/s)3 = 2*n3/p3/2
left-circular-shift each row of A by 1 … cost = a + b*n2/p
up-circular-shift each column of B by 1 … cost = a + b*n2/p
° Total Time = 2*n3/p + 4* s*a + 4*b*n2/s
° Parallel Efficiency = 2*n3 / (p * Total Time)
= 1/( 1 + a * 2*(s/n)3 + b * 2*(s/n) )
= 1/(1 + O(sqrt(p)/n))
° Grows to 1 as n/s = n/sqrt(p) = sqrt(data per processor) grows
° Better than 1D layout, which had Efficiency = 1/(1 + O(p/n))
3/02/2010
CS267 Lecture 13
50
Cannon’s Algorithm is “optimal”
• Optimal means
• Considering only O(n3) matmul algs (not Strassen)
• Considering only O(n2/p) storage per processor
• Use communication lower bound #words = (#flops/M1/2)
• Sequential: a processor doing n3 flops from matmul
with a fast memory of size M must do (n3 / M1/2 )
references to slow memory
• Parallel: a processor doing f =#flops from matmul with
a local memory of size M must do (f / M1/2 )
references to remote memory
• Local memory = O(n2/p) , f n3/p for at least one proc.
• So f / M1/2 = ((n3/p)/ (n2/p)1/2 ) = ( n2/p1/2 )
• #Messages = ( #words sent / max message size) =
( (n2/p1/2)/(n2/p)) = (p1/2)
3/02/2010
CS267 Lecture 13
51
Pros and Cons of Cannon
• So what if it’s “optimal”, is it fast?
• Local computation one call to (optimized) matrix-multiply
• Hard to generalize for
• p not a perfect square
• A and B not square
• Dimensions of A, B not perfectly divisible by
s=sqrt(p)
• A and B not “aligned” in the way they are stored on
processors
• block-cyclic layouts
• Memory hog (extra copies of local matrices)
3/02/2010
CS267 Lecture 13
52
SUMMA Algorithm
• SUMMA = Scalable Universal Matrix Multiply
• Slightly less efficient, but simpler and easier to generalize
• Presentation from van de Geijn and Watts
• www.netlib.org/lapack/lawns/lawn96.ps
• Similar ideas appeared many times
• Used in practice in PBLAS = Parallel BLAS
• www.netlib.org/lapack/lawns/lawn100.ps
3/02/2010
CS267 Lecture 13
53
SUMMA
k
j
B(k,j)
k
i
*
=
C(i,j)
A(i,k)
i, j represent all rows, columns owned by a processor
• k is a block of b 1 rows or columns
•
• C(i,j) = C(i,j) + Sk A(i,k)*B(k,j)
• Assume a pr by pc processor grid (pr = pc = 4 above)
• Need not be square
3/02/2010
CS267 Lecture 13
54
SUMMA
k
j
B(k,j)
k
*
i
=
C(i,j)
A(i,k)
For k=0 to n/b-1
… where b is the block size
… b = # cols in A(i,k) and # rows in B(k,j)
for all i = 1 to pr … in parallel
owner of A(i,k) broadcasts it to whole processor row
for all j = 1 to pc … in parallel
owner of B(k,j) broadcasts it to whole processor column
Receive A(i,k) into Acol
Receive B(k,j) into Brow
C_myproc = C_myproc + Acol * Brow
3/02/2010
CS267 Lecture 13
55
SUMMA performance
° To simplify analysis only, assume s = sqrt(p)
For k=0 to n/b-1
for all i = 1 to s … s = sqrt(p)
owner of A(i,k) broadcasts it to whole processor row
… time = log s *( a + b * b*n/s), using a tree
for all j = 1 to s
owner of B(k,j) broadcasts it to whole processor column
… time = log s *( a + b * b*n/s), using a tree
Receive A(i,k) into Acol
Receive B(k,j) into Brow
C_myproc = C_myproc + Acol * Brow
… time = 2*(n/s)2*b
° Total time = 2*n3/p + a * log p * n/b + b * log p * n2 /s
3/02/2010
CS267 Lecture 13
56
SUMMA performance
• Total time = 2*n3/p + a * log p * n/b + b * log p * n2 /s
• Parallel Efficiency =
1/(1 + a * log p * p / (2*b*n2) + b * log p * s/(2*n) )
• Same b term as Cannon, except for log p factor
log p grows slowly so this is ok
• Latency (a) term can be larger, depending on b
When b=1, get a * log p * n
As b grows to n/s, term shrinks to
a * log p * s (log p times Cannon)
• Temporary storage grows like 2*b*n/s
• Can change b to tradeoff latency cost with memory
3/02/2010
CS267 Lecture 13
57
PDGEMM = PBLAS routine
for matrix multiply
Observations:
For fixed N, as P increases
Mflops increases, but
less than 100% efficiency
For fixed P, as N increases,
Mflops (efficiency) rises
DGEMM = BLAS routine
for matrix multiply
Maximum speed for PDGEMM
= # Procs * speed of DGEMM
Observations (same as above):
Efficiency always at least 48%
For fixed N, as P increases,
efficiency drops
For fixed P, as N increases,
efficiency increases
3/02/2010
CS267 Lecture 8
58
Summary of Parallel Matrix Multiplication
• 1D Layout
• Bus without broadcast - slower than serial
• Nearest neighbor communication on a ring (or bus with
broadcast): Efficiency = 1/(1 + O(p/n))
• 2D Layout
• Cannon
• Efficiency = 1/(1+O(a * ( sqrt(p) /n)3 +b* sqrt(p) /n)) – optimal!
• Hard to generalize for general p, n, block cyclic, alignment
• SUMMA
•
•
•
•
•
Efficiency = 1/(1 + O(a * log p * p / (b*n2) + b*log p * sqrt(p) /n))
Very General
b small => less memory, lower efficiency
b large => more memory, high efficiency
Used in practice (PBLAS)
3/02/2010
CS267 Lecture 13
59
ScaLAPACK Parallel Library
3/02/2010
CS267 Lecture 13
60
Extra Slides
3/02/2010
CS267 Lecture 13
61
Recursive Layouts
• For both cache hierarchies and parallelism, recursive
layouts may be useful
• Z-Morton, U-Morton, and X-Morton Layout
• Also Hilbert layout and others
• What about the user’s view?
• Fortunately, many problems can be solved on a
permutation
• Never need to actually change the user’s layout
2/27/08
CS267 Guest Lecture 1
62
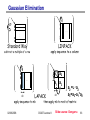
Gaussian Elimination
x
0
x
x
x
x
0
0
.
.
.
0
0
Standard Way
LINPACK
apply sequence to a column
subtract a multiple of a row
x
x
0
0
...
nb
L
a2
a1 a3
0
0
LAPACK
apply sequence to nb
02/09/2006
...
nb
a2 =L-1 a2
a3=a3-a1*a2
then apply nb to rest of matrix
CS267 Lecture 8
Slide source: Dongarra
63
Gaussian Elimination via a Recursive Algorithm
F. Gustavson and S. Toledo
LU Algorithm:
1: Split matrix into two rectangles (m x n/2)
if only 1 column, scale by reciprocal of pivot & return
2: Apply LU Algorithm to the left part
3: Apply transformations to right part
(triangular solve A12 = L-1A12 and
matrix multiplication A22=A22 -A21*A12 )
4: Apply LU Algorithm to right part
L
A12
A21
A22
Most of the work in the matrix multiply
Matrices of size n/2, n/4, n/8, …
02/09/2006
CS267 Lecture 8
Slide source: Dongarra
64
Recursive Factorizations
• Just as accurate as conventional method
• Same number of operations
• Automatic variable blocking
• Level 1 and 3 BLAS only !
• Extreme clarity and simplicity of expression
• Highly efficient
• The recursive formulation is just a rearrangement of the point-wise
LINPACK algorithm
• The standard error analysis applies (assuming the matrix
operations are computed the “conventional” way).
02/09/2006
CS267 Lecture 8
Slide source: Dongarra
65
DGEMM
& DGETRF
Recursive
PentiumATLAS
III 550 MHz
Dual Processor
LU 1GHz
Factorization
AMD Athlon
(~$1100
system)
Recursive
LU
MFlop/s
Mflop/s
800
Dual-processor
400
600
300
400
200
200
100
LAPACK
Recursive LU
LAPACK
Uniprocessor
00
500
1500
500 1000 1000
2000 15002500
3000
2000 3500
4000
2500
4500 3000
5000
Order
Order
02/09/2006
CS267 Lecture 8
Slide source: Dongarra
66
Review: BLAS 3 (Blocked) GEPP
for ib = 1 to n-1 step b … Process matrix b columns at a time
end = ib + b-1
… Point to end of block of b columns
apply BLAS2 version of GEPP to get A(ib:n , ib:end) = P’ * L’ * U’
… let LL denote the strict lower triangular part of A(ib:end , ib:end) + I
A(ib:end , end+1:n) = LL-1 * A(ib:end , end+1:n)
… update next b rows of U
A(end+1:n , end+1:n ) = A(end+1:n , end+1:n )
BLAS 3
- A(end+1:n , ib:end) * A(ib:end , end+1:n)
… apply delayed updates with single matrix-multiply
… with inner dimension b
02/09/2006
CS267 Lecture 8
67
Review: Row and Column Block Cyclic Layout
processors and matrix blocks
are distributed in a 2d array
pcol-fold parallelism
in any column, and calls to the
BLAS2 and BLAS3 on matrices of
size brow-by-bcol
serial bottleneck is eased
need not be symmetric in rows and
columns
02/09/2006
CS267 Lecture 8
68
Distributed GE with a 2D Block Cyclic Layout
block size b in the algorithm and the block sizes brow
and bcol in the layout satisfy b=brow=bcol.
shaded regions indicate busy processors or
communication performed.
unnecessary to have a barrier between each
step of the algorithm, e.g.. step 9, 10, and 11 can be
pipelined
02/09/2006
CS267 Lecture 8
69
Distributed GE with a 2D Block Cyclic Layout
02/09/2006
CS267 Lecture 8
70
02/09/2006
CS267 Lecture 8
71
green = green - blue * pink
Matrix multiply of
PDGESV = ScaLAPACK
parallel LU routine
Since it can run no faster than its
inner loop (PDGEMM), we measure:
Efficiency =
Speed(PDGESV)/Speed(PDGEMM)
Observations:
Efficiency well above 50% for large
enough problems
For fixed N, as P increases,
efficiency decreases
(just as for PDGEMM)
For fixed P, as N increases
efficiency increases
(just as for PDGEMM)
From bottom table, cost of solving
Ax=b about half of matrix multiply
for large enough matrices.
From the flop counts we would
expect it to be (2*n3)/(2/3*n3) = 3
times faster, but communication
makes it a little slower.
02/09/2006
CS267 Lecture 8
72
02/09/2006
CS267 Lecture 8
73
Scales well,
nearly full machine speed
02/09/2006
CS267 Lecture 8
74
Old version,
pre 1998 Gordon Bell Prize
Still have ideas to accelerate
Project Available!
Old Algorithm,
plan to abandon
02/09/2006
CS267 Lecture 8
75
Have good ideas to speedup
Project available!
Hardest of all to parallelize
Have alternative, and
would like to compare
Project available!
02/09/2006
CS267 Lecture 8
76
Out-of-core means
matrix lives on disk;
too big for main mem
Much harder to hide
latency of disk
QR much easier than LU
because no pivoting
needed for QR
Moral: use QR to solve Ax=b
Projects available
(perhaps very hard…)
02/09/2006
CS267 Lecture 8
77
A small software project ...
02/09/2006
CS267 Lecture 8
78
Work-Depth Model of Parallelism
• The work depth model:
• The simplest model is used
• For algorithm design, independent of a machine
• The work, W, is the total number of operations
• The depth, D, is the longest chain of dependencies
• The parallelism, P, is defined as W/D
• Specific examples include:
• circuit model, each input defines a graph with ops at
nodes
• vector model, each step is an operation on a vector of
elements
• language model, where set of operations defined by
language
02/09/2006
CS267 Lecture 8
79
Latency Bandwidth Model
• Network of fixed number P of processors
• fully connected
• each with local memory
• Latency (a)
• accounts for varying performance with number of
messages
• gap (g) in logP model may be more accurate cost if
messages are pipelined
• Inverse bandwidth (b)
• accounts for performance varying with volume of data
• Efficiency (in any model):
• serial time / (p * parallel time)
• perfect (linear) speedup efficiency = 1
02/09/2006
CS267 Lecture 8
80
Initial Step to Skew Matrices in Cannon
• Initial blocked input
A(0,0) A(0,1) A(0,2)
B(0,0) B(0,1) B(0,2)
A(1,0) A(1,1) A(1,2)
B(1,0) B(1,1) B(1,2)
A(2,0) A(2,1) A(2,2)
B(2,0) B(2,1) B(2,2)
• After skewing before initial block multiplies
A(0,0) A(0,1) A(0,2)
B(0,0) B(1,1) B(2,2)
A(1,1) A(1,2) A(1,0)
B(1,0) B(2,1) B(0,2)
A(2,2) A(2,0) A(2,1)
B(2,0) B(0,1) B(1,2)
02/09/2006
CS267 Lecture 8
81
Skewing Steps in Cannon
• First step
• Second
• Third
02/09/2006
A(0,0) A(0,1) A(0,2)
B(0,0) B(1,1) B(2,2)
A(1,1) A(1,2) A(1,0)
B(1,0) B(2,1) B(0,2)
A(2,2) A(2,0) A(2,1)
B(2,0) B(0,1) B(1,2)
A(0,1) A(0,2) A(0,0)
B(1,0) B(2,1) B(0,2)
A(1,2) A(1,0) A(1,1)
B(2,0) B(0,1) B(1,2)
A(2,0) A(2,1) A(2,2)
B(0,0) B(1,1) B(2,2)
A(0,2) A(0,0) A(0,1)
B(2,0) B(0,1) B(1,2)
A(1,0) A(1,1) A(1,2)
B(0,0) B(1,1) B(2,2)
A(2,1) A(2,2) A(2,0)
CS267 Lecture 8
B(1,0) B(2,1) B(0,2)
82
Motivation (1)
3 Basic Linear Algebra Problems
1. Linear Equations: Solve Ax=b for x
2. Least Squares: Find x that minimizes ||r||2 S ri2
where r=Ax-b
• Statistics: Fitting data with simple functions
3a. Eigenvalues: Find l and x where Ax = l x
• Vibration analysis, e.g., earthquakes, circuits
3b. Singular Value Decomposition: ATAx=2x
• Data fitting, Information retrieval
Lots of variations depending on structure of A
• A symmetric, positive definite, banded, …
2/25/2009
CS267 Lecture 8
83
Motivation (2)
• Why dense A, as opposed to sparse A?
• Many large matrices are sparse, but …
• Dense algorithms easier to understand
• Some applications yields large dense
matrices
• LINPACK Benchmark (www.top500.org)
• “How fast is your computer?” =
“How fast can you solve dense Ax=b?”
• Large sparse matrix algorithms often yield
smaller (but still large) dense problems
• Do ParLab Apps most use small dense matrices?
2/25/2009
CS267 Lecture 8
84
Algorithms for 2D (3D) Poisson Equation (N = n2 (n3) vars)
Algorithm
Serial
• Dense LU
N3
• Band LU
N2 (N7/3)
• Jacobi
N2 (N5/3)
• Explicit Inv.
N2
• Conj.Gradients N3/2 (N4/3)
• Red/Black SOR N3/2 (N4/3)
• Sparse LU
N3/2 (N2)
• FFT
N*log N
• Multigrid
N
• Lower bound N
PRAM
N
N
N (N2/3)
log N
N1/2(1/3) *log N
N1/2 (N1/3)
N1/2
log N
log2 N
log N
Memory
N2
N3/2 (N5/3)
N
N2
N
N
N*log N (N4/3)
N
N
N
#Procs
N2
N (N4/3)
N
N2
N
N
N
N
N
PRAM is an idealized parallel model with zero cost communication
Reference: James Demmel, Applied Numerical Linear Algebra, SIAM, 1997
(Note: corrected complexities for 3D case from last lecture!).
02/25/2009
CS267 Lecture 8
Lessons and Questions (1)
• Structure of the problem matters
• Cost of solution can vary dramatically (n3 to n)
• Many other examples
• Some structure can be figured out automatically
• “A\b” can figure out symmetry, some sparsity
• Some structures known only to (smart) user
• If performance not critical, user may be happy to settle for A\b
• How much of this goes into the motifs?
• How much should we try to help user choose?
• Tuning, but at algorithmic choice level (SALSA)
• Motifs overlap
• Dense, sparse, (un)structured grids, spectral
Organizing Linear Algebra (1)
• By Operations
• Low level (eg mat-mul: BLAS)
• Standard level (eg solve Ax=b, Ax=λx: Sca/LAPACK)
• Applications level (eg systems & control: SLICOT)
• By Performance/accuracy tradeoffs
• “Direct methods” with guarantees vs “iterative methods” that
may work faster and accurately enough
• By Structure
• Storage
•
•
Dense
– columnwise, rowwise, 2D block cyclic, recursive space-filling curves
Banded, sparse (many flavors), black-box, …
• Mathematical
•
•
Symmetries, positive definiteness, conditioning, …
As diverse as the world being modeled
Organizing Linear Algebra (2)
• By Data Type
• Real vs Complex
• Floating point (fixed or varying length), other
• By Target Platform
• Serial, manycore, GPU, distributed memory, out-ofDRAM, Grid, …
• By programming interface
• Language bindings
• “A\b” versus access to details
For all linear algebra problems:
Ex: LAPACK Table of Contents
• Linear Systems
• Least Squares
• Overdetermined, underdetermined
• Unconstrained, constrained, weighted
• Eigenvalues and vectors of Symmetric Matrices
•
Standard (Ax = λx), Generallzed (Ax=λxB)
• Eigenvalues and vectors of Unsymmetric matrices
•
•
Eigenvalues, Schur form, eigenvectors, invariant subspaces
Standard, Generalized
• Singular Values and vectors (SVD)
• Standard, Generalized
• Level of detail
• Simple Driver
• Expert Drivers with error bounds, extra-precision, other options
• Lower level routines (“apply certain kind of orthogonal transformation”)
For all matrix/problem structures:
Ex: LAPACK Table of Contents
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
BD – bidiagonal
GB – general banded
GE – general
GG – general , pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
•
•
•
•
•
•
•
•
•
•
•
•
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
For all matrix/problem structures:
Ex: LAPACK Table of Contents
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
BD – bidiagonal
GB – general banded
GE – general
GG – general , pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
•
•
•
•
•
•
•
•
•
•
•
•
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
For all matrix/problem structures:
Ex: LAPACK Table of Contents
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
BD – bidiagonal
GB – general banded
GE – general
GG – general, pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
•
•
•
•
•
•
•
•
•
•
•
•
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
For all matrix/problem structures:
Ex: LAPACK Table of Contents
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
BD – bidiagonal
GB – general banded
GE – general
GG – general, pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
•
•
•
•
•
•
•
•
•
•
•
•
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
For all matrix/problem structures:
Ex: LAPACK Table of Contents
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
BD – bidiagonal
GB – general banded
GE – general
GG – general, pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
•
•
•
•
•
•
•
•
•
•
•
•
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
For all matrix/problem structures:
Ex: LAPACK Table of Contents
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
BD – bidiagonal
GB – general banded
GE – general
GG – general , pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
•
•
•
•
•
•
•
•
•
•
•
•
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
For all matrix/problem structures:
Ex: LAPACK Table of Contents
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
BD – bidiagonal
GB – general banded
GE – general
GG – general, pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
•
•
•
•
•
•
•
•
•
•
•
•
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
For all data types:
Ex: LAPACK Table of Contents
• Real and complex
• Single and double precision
• Arbitrary precision in progress
Organizing Linear Algebra (3)
www.netlib.org/lapack
www.netlib.org/scalapack
gams.nist.gov
www.netlib.org/templates
www.cs.utk.edu/~dongarra/etemplates
Review of the BLAS
• Building blocks for all linear algebra
• Parallel versions call serial versions on each processor
• So they must be fast!
• Define q = # flops / # mem refs = “computational intensity”
• The larger is q, the faster the algorithm can go in the
presence of memory hierarchy
• “axpy”: y = a*x + y, where a scalar, x and y vectors
BLAS level
Ex.
# mem refs
# flops
q
1
“Axpy”,
Dot prod
3n
2n1
2/3
2
Matrixvector mult
n2
2n2
2
3
Matrixmatrix mult
4n2
2n3
n/2
2/27/08
CS267 Guest Lecture 1
99