* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download math 214 (notes) - Department of Mathematics and Statistics
Survey
Document related concepts
Transcript
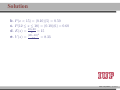
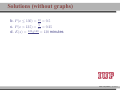
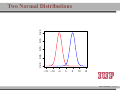
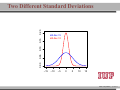
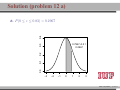
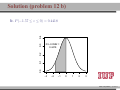
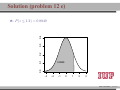
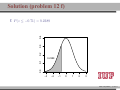
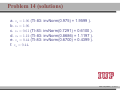
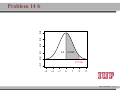
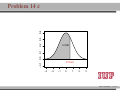
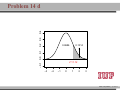
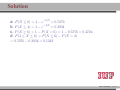
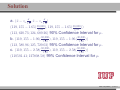
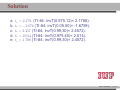
MATH 214 (NOTES) Math 214 Al Nosedal Department of Mathematics Indiana University of Pennsylvania MATH 214 (NOTES) – p. 1/11 CHAPTER 6 CONTINUOUS PROBABILITY DISTRIBUTIONS MATH 214 (NOTES) – p. 2/11 Simple example Random Experiment: Rolling a fair die 300 times. Class 1≤x<2 2≤x<3 3≤x<4 4≤x<5 5≤x<6 6≤x<7 Expected Freq. Expected Relative Freq. 50 1/6 50 1/6 50 1/6 50 1/6 50 1/6 50 1/6 MATH 214 (NOTES) – p. 3/11 Histogram 50 40 30 freq 60 70 Histogram of frequencies 1 2 3 4 5 6 7 MATH 214 (NOTES) – p. 4/11 Histogram (Relative Freqs.) 0.18 0.14 0.10 freq 0.22 Histogram of Relative Frequencies 1 2 3 4 5 6 7 MATH 214 (NOTES) – p. 5/11 Uniform Probability Distribution Uniform Probability Density Function 1 f (x) = b−a f (x) = 0 for a ≤ x ≤ b elsewhere MATH 214 (NOTES) – p. 6/11 Expected Value and Variance a+b E(X) = 2 (b − a)2 V ar(X) = 12 MATH 214 (NOTES) – p. 7/11 Problem 2 (page 230) The random variable x is known to be uniformly distributed between 10 and 20. a. Show the graph of the probability density function. b. Compute P (x < 15). c. Compute P (12 ≤ x ≤ 18). d. Compute E(x). e. Compute V ar(x). MATH 214 (NOTES) – p. 8/11 Solution 0.10 0.08 0.06 f(x) 0.12 0.14 Graph of Probability Density Function 10 12 14 16 18 20 MATH 214 (NOTES) – p. 9/11 Solution b. P (x < 15) = (0.10)(5) = 0.50 c. P (12 ≤ x ≤ 18) = (0.10)(6) = 0.60 = 15 d. E(x) = 10+20 2 e. V (x) = (20−10)2 12 = 8.33 MATH 214 (NOTES) – p. 10/11 Problem 3 (page 230) Delta Airlines quotes a flight time of 2 hours, 5 minutes for its flights from Cincinnati to Tampa. Suppose we believe that actual flight times are uniformly distributed between 2 hours and 2 hours, 20 minutes. a. Show the graph of the probability density function for flight time. b. What is the probability that the flight will be no more than 5 minutes late? c. What is the probability that the flight will be more than 10 minutes late? d. What is the expected flight time? MATH 214 (NOTES) – p. 11/11 Solution (problem 3 a) 0.05 0.04 0.03 f(x) 0.06 0.07 Graph of Probability Density Function 120 125 130 135 140 minutes MATH 214 (NOTES) – p. 12/11 Solution (problem 3 b) 10 20 = 0.5 0.05 0.04 0.03 f(x) 0.06 0.07 b. P (x ≤ 130) = 120 125 130 135 140 minutes MATH 214 (NOTES) – p. 13/11 Solution (problem 3 c) 5 20 = 0.25 0.05 0.04 0.03 f(x) 0.06 0.07 c. P (x > 135) = 120 125 130 135 140 minutes MATH 214 (NOTES) – p. 14/11 Solutions (without graphs) 10 = 0.5 b. P (x ≤ 130) = 20 5 = 0.25 c. P (x > 135) = 20 = 130 minutes d. E(x) = 120+140 2 MATH 214 (NOTES) – p. 15/11 Standard Normal Probability Distribution 0.0 0.1 0.2 0.3 0.4 Normal Distribution mean=0 and std.dev.=1 −3 −2 −1 0 1 2 3 MATH 214 (NOTES) – p. 16/11 Standard Normal Probability Distribution 1 −z2 f (z) = √ e 2 2π Note. Don’t worry about this formula, we are NOT going to use it to do calculations. MATH 214 (NOTES) – p. 17/11 Normal Probability Density Function −(x−µ)2 1 f (x) = √ e 2σ2 σ 2π where µ = mean, σ = standard deviation, e = 2.71828 and π = 3.14159. Note. Don’t worry about this formula, we are NOT going to use it to do calculations. MATH 214 (NOTES) – p. 18/11 0.00 0.05 0.10 0.15 0.20 Two Normal Distributions −15 −10 −5 0 5 10 15 MATH 214 (NOTES) – p. 19/11 0.20 Two Different Standard Deviations 0.00 0.05 0.10 0.15 std.dev.=5 std.dev.=2 −15 −10 −5 0 5 10 15 MATH 214 (NOTES) – p. 20/11 Problem 11 (page 241) Given that z is a standard normal random variable, compute the following probabilities. a. P (z ≤ −1). b. P (z ≥ −1) c. P (z ≥ −1.5) d. P (−2.5 ≤ z) e. P (−3 < z ≤ 0) MATH 214 (NOTES) – p. 21/11 Problem 12 (page 241) Given that z is a standard normal random variable, compute the following probabilities. a. P (0 ≤ z ≤ 0.83) b. P (−1.57 ≤ z ≤ 0) c. P (z ≥ 0.44) d. P (z ≥ −0.23) e. P (z ≤ 1.2) f. P (z ≤ −0.71) MATH 214 (NOTES) – p. 22/11 Solution (problem 12 a) 0.4 a. P (0 ≤ z ≤ 0.83) = 0.2967 0.0 0.1 0.2 0.3 0.7967−0.5 = 0.2967 −3 −2 −1 0 1 2 3 MATH 214 (NOTES) – p. 23/11 Solution (problem 12 b) 0.5−0.0582 = 0.4418 0.0 0.1 0.2 0.3 0.4 b. P (−1.57 ≤ z ≤ 0) = 0.4418 −3 −2 −1 0 1 2 3 MATH 214 (NOTES) – p. 24/11 Solution (problem 12 c) 0.4 c. P (z ≥ 0.44) = 0.3300 0.1 0.2 0.3 1−0.6700 = 0.3300 0.0 0.6700 −3 −2 −1 0 1 2 3 MATH 214 (NOTES) – p. 25/11 Solution (problem 12 d) 0.4 d. P (z ≥ −0.23) = 0.5910 0.1 0.2 0.3 1−0.4090 = 0.5910 0.0 0.4090 −3 −2 −1 0 1 2 3 MATH 214 (NOTES) – p. 26/11 Solution (problem 12 e) 0.1 0.2 0.3 0.4 e. P (z ≤ 1.2) = 0.8849 0.0 0.8849 −3 −2 −1 0 1 2 3 MATH 214 (NOTES) – p. 27/11 Solution (problem 12 f) 0.2 0.3 0.4 f. P (z ≤ −0.71) = 0.2389 0.0 0.1 0.2389 −3 −2 −1 0 1 2 3 MATH 214 (NOTES) – p. 28/11 Problem 14 (page 241) Given that Z is a standard normal random variable, find z∗ for each situation. a. The area to the left of z∗ is 0.9750. b. The area between 0 and z∗ is 0.4750. c. The area to the left of z∗ is 0.7291. d. The area to the right of z∗ is 0.1314. e. The area to the left of z∗ is 0.6700. f. The area to the right of z∗ is 0.3300. MATH 214 (NOTES) – p. 29/11 Problem 14 (solutions) a. z∗ = 1.96 (TI-83: invNorm(0.975) = 1.9599 ). b. z∗ = 1.96 c. z∗ = 0.61 (TI-83: invNorm(0.7291) = 0.6100 ). d. z∗ = 1.12 (TI-83: invNorm(0.8686) = 1.1197 ). e. z∗ = 0.44 (TI-83: invNorm(0.6700) = 0.4399 ). f. z∗ = 0.44. MATH 214 (NOTES) – p. 30/11 0.2 0.3 0.4 Problem 14 a 0.0 0.1 0.9750 −0.1 z*=1.96 −3 −2 −1 0 1 2 3 MATH 214 (NOTES) – p. 31/11 0.1 0.2 0.3 0.4 Problem 14 b 0.4750 0.0 0.5 −0.1 z*=1.96 −3 −2 −1 0 1 2 3 MATH 214 (NOTES) – p. 32/11 0.2 0.3 0.4 Problem 14 c 0.0 0.1 0.7291 −0.1 z*=0.61 −3 −2 −1 0 1 2 3 MATH 214 (NOTES) – p. 33/11 0.2 0.3 0.4 Problem 14 d 0.1314 0.0 0.1 0.8686 −0.1 z*=1.12 −3 −2 −1 0 1 2 3 MATH 214 (NOTES) – p. 34/11 0.1 0.2 0.3 0.4 Problem 14 e 0.0 0.67 −0.1 z*=0.44 −3 −2 −1 0 1 2 3 MATH 214 (NOTES) – p. 35/11 0.1 0.2 0.3 0.4 Problem 14 f 0.33 0.0 0.67 −0.1 z*=0.44 −3 −2 −1 0 1 2 3 MATH 214 (NOTES) – p. 36/11 Problem 15 (page 242) Given that z is a standard normal random variable, find z for each situation. a. The area to the left of z∗ is 0.2119. b. The area between −z∗ and z∗ is 0.9030. c. The area between −z∗ and z∗ is 0.2052. d. The area to the left of z∗ is 0.9948. e. The area to the right of z∗ is 0.6915. MATH 214 (NOTES) – p. 37/11 Problem 15 (solutions) a. z∗ = −0.80. b. z∗ = 1.66. c z∗ = 0.26. d. z∗ = 2.56. e. z∗ = −0.50. MATH 214 (NOTES) – p. 38/11 Problem 17 (page 242) For borrowers with good credit scores, the mean debt for revolving and installment accounts is $ 15,015. Assume the standard deviation is $ 3540 and that debt amounts are normally distributed. a. What is the probability that the debt for a randomly selected borrower with good credit is more than $ 18,000? b. What is the probability that the debt for a randomly selected borrower with good credit is less than $ 10,000? c. What is the probability that the debt for a randomly selected borrower with good credit is between $ 12,000 and $ 18,000? d. What is the probability that the debt for a randomly selected borrower with good credit is no more than $ 14,000? MATH 214 (NOTES) – p. 39/11 Problem 17 (solutions) Let X = debt amount. a. P (X > 18000) = P ( X−µ σ > 18000−15015 ) 3540 = P (Z > 0.8432) = 1 − P (Z < 0.8432) = 1 − 0.7995 = 0.2005 10000−15015 < ) = P (Z < −1.4166) w b. P (X < 10000) = P ( X−µ σ 3540 0.0773 c. P (12000 < X < 18000) = X−µ 18000−15015 < < ) = P (−0.8516 < Z < 0.8432) = P ( 12000−15015 3540 σ 3540 P (Z < 0.8432) − P (Z < −0.8516) w 0.7995 − 0.1977 = 0.6018 14000−15015 d. P (X ≤ 14000) = P ( X−µ ≤ ) = P (Z < −0.2867) w σ 3540 0.3897 MATH 214 (NOTES) – p. 40/11 Problem 21 (page 242) A person must score in the upper 2% of the population on an IQ test to qualify for membership in MENSA, the international high-IQ society. If IQ scores are normally distributed with a mean of 100 and a standard deviation of 15, what score must a person have to qualify for MENSA?. MATH 214 (NOTES) – p. 41/11 Problem 21 (solution) 1. State the problem. Let X = IQ score of a randomly selected person. We want to find the IQ score x∗ with area 0.02 to its right under the Normal curve with mean µ = 100 and standard deviation σ = 15. That’s the same as finding the IQ score x∗ with area 0.98 to its left. Because our table gives the areas to the left of z-values, always state the problem in terms of the area to the left of x∗ . MATH 214 (NOTES) – p. 42/11 Solution (cont.) 2. Use the table. Look in the body of our table for the entry closest to 0.98. It is 0.9798. This is the entry corresponding to z∗ = 2.05. So z∗ = 2.05 is the standardized value with area 0.98 to its left. 3. Unstandardize to transform the solution from the Z back to the original X scale. We know that the standardized value of the unknown x∗ is z∗ = 2.05. So x∗ itself satisfies: x∗ −100 = 2.05. Solving this equation for x∗ gives: 15 x∗ = 100 + (2.05)(15) = 130.75. We see that a person must score at least 130.75 (131 perhaps) to place in the highest 2%. MATH 214 (NOTES) – p. 43/11 Problem 25 (page 243) According to the Sleep Foundation, the average night’s sleep is 6.8 hours. Assume the standard deviation is 0.6 hours and that the probability distribution is normal. a. What is the probability that a randomly selected person sleeps more than 8 hours? b. What is the probability that a randomly selected person sleeps 6 hours or less? c. Doctors suggest getting between 7 and 9 hours of sleep each night. What percentage of the population gets this much sleep? MATH 214 (NOTES) – p. 44/11 Problem 25 (solution) Let X = number of hours a randomly selected person sleeps per night. 8−6.8 a. P (X > 8) = P ( X−µ > σ 0.6 ) = P (Z > 2) = 1 − 0.9772 = 0.0228 6−6.8 ≤ b.P (X ≤ 6) = P ( X−µ σ 0.6 ) = P (Z ≤ −1.33) = 0.0918 X−µ 9−6.8 c.P (7 ≤ X ≤ 9) = P ( 7−6.8 ≤ ≤ 0.6 σ 0.6 ) = P (0.33 ≤ Z < 3.66) ' 1 − 0.6293 = 0.3707 MATH 214 (NOTES) – p. 45/11 Standard Normal Distribution (again) The Standard Normal Distribution is the Normal Distribution N (0, 1) with mean 0 and standard deviation 1. If a variable X has any Normal Distribution N (µ, σ) with mean µ and standard deviation σ , then the standardized variable X −µ Z= σ has the Standard Normal Distribution. MATH 214 (NOTES) – p. 46/11 Finding Normal Probabilities 1. State the problem in terms of the observed variable X . 2. Standardize X to restate the problem in terms of a Standard Normal variable Z . Draw a picture to show the area under the Standard Normal curve. 3. Find the required area under the Standard Normal curve, using a table (or a calculator) and the fact that the total area under the curve is 1. MATH 214 (NOTES) – p. 47/11 Exponential Probability Distribution EXPONENTIAL PROBABILITY DENSITY FUNCTION 1 −x f (x) = e µ µ for x ≥ 0 and µ ≥ 0 (where µ = expected value or mean) MATH 214 (NOTES) – p. 48/11 Exponential Distribution (cont.) CUMULATIVE PROBABILITIES. P (X ≤ k) = 1 − e−k/µ MATH 214 (NOTES) – p. 49/11 Problem 32 (page 249) Consider the following exponential probability density function. 1 −x/8 f (x) = e 8 a. Find P (X ≤ 6). b. Find P (X ≤ 4). c. Find P (X ≥ 6). d. Find P (4 ≤ X ≤ 6). MATH 214 (NOTES) – p. 50/11 Solution a. P (X ≤ 6) = 1 − e−6/8 = 0.5276 b. P (X ≤ 4) = 1 − e−4/8 = 0.3934 c. P (X ≥ 6) = 1 − P (X < 6) = 1 − 0.5276 = 0.4724 d. P (4 ≤ X ≤ 6) = P (X ≤ 6) − P (X < 4) = 0.5276 − 0.3934 = 0.1342 MATH 214 (NOTES) – p. 51/11 Problem 34 (page 249) The time required to pass through security screening at the airport can be annoying to travelers. The mean wait time during peak periods at Cincinnati/Northern Kentucky International Airport is 12.1 minutes. Assume the time to pass through security screening follows an exponential distribution. a. What is the probability it will take less than 10 minutes to pass through security screening during a peak period? MATH 214 (NOTES) – p. 52/11 Problem 34 (cont.) b. What is the probability it will take more than 20 minutes to pass through security screening during a peak period? c. What is the probability it will take between 10 and 20 minutes to pass through security screening during a peak period? d. It is 8:00 a.m. (a peak period) and you just entered the security line. To catch your plane you must be at the gate within 30 minutes. If it takes 12 minutes from the time you clear security until you reach your gate, what is the probability you will miss your flight? MATH 214 (NOTES) – p. 53/11 Solution Let T be the time required to pass through security screening. T has an exponential distribution with µ = 12.1 a. P (T < 10) = 1 − e−10/12.1 = 0.5623 b. P (T > 20) = 1 − P (T ≤ 20) = 1 − (1 − e−20/12.1 ) = 1 − 0.8085 = 0.1915 c. P (10 < T < 20) = P (T < 20) − P (T < 10) = 0.8085 − 0.5623 = 0.2462 d. P (missing your flight) = P (T > 18) = 1 − P (T ≤ 18) = 1 − (1 − e−18/12.1 ) = 1 − 0.7740 = 0.226 MATH 214 (NOTES) – p. 54/11 CHAPTER 7 SAMPLING AND SAMPLING DISTRIBUTIONS MATH 214 (NOTES) – p. 55/11 Toy example Consider a population of 5 families with annual incomes shown below. We want to choose a simple random sample of size 2 from this population. How can this be done? And how do the sample mean of the chosen families compare to population mean? Incomes: 30,000 35,000 40,000 45,000 50,000. MATH 214 (NOTES) – p. 56/11 Solution 30,000+40,000 x̄1 = 30,000+35,000 = 32, 500 x̄ = = 35, 000 2 2 2 30,000+50,000 x̄3 = 30,000+45,000 = 37, 500 x̄ = = 40, 000 4 2 2 35,000+45,000 = 37, 500 x̄ = = 40, 000 x̄5 = 35,000+40,000 6 2 2 40,000+45,000 x̄7 = 35,000+50,000 = 42, 500 x̄ = = 42, 500 8 2 2 45,000+50,000 = 45, 000 x̄ = = 47, 500 x̄9 = 40,000+50,000 10 2 2 µ = 40, 000 (population mean). MATH 214 (NOTES) – p. 57/11 1.0 0.5 0.0 frequency 1.5 2.0 Graph 32500 37500 42500 47500 income MATH 214 (NOTES) – p. 58/11 Population, Sample The entire group of individuals that we want information about is called the population. A sample is a part of the population that we actually examine in order to gather information. MATH 214 (NOTES) – p. 59/11 Simple Random Sample A simple random sample (SRS) of size n consists of n individuals from the population chosen in such a way that every set of n individuals has an equal chance to be the sample actually selected. MATH 214 (NOTES) – p. 60/11 Example A couple plans to have three children. There are 8 possible arrangements of girls and boys. For example, GGB means the first two children are girls and the third child is a boy. All 8 arrangements are (approximately) equally likely. a) Write down all 8 arrangements of the sexes of three children. What is the probability of any one of these arrangements? MATH 214 (NOTES) – p. 61/11 Example (cont.) b) Let X be the number of girls the couple has. What is the probability that X = 2 ? c) Starting from your work in a), find the distribution of X . That is, what values can X take, and what are the probabilities for each value? MATH 214 (NOTES) – p. 62/11 Binomial Probability Function n! f (x) = px (1 − p)n−x x!(n − x)! f (x)= the probability of x successes in n trials. n= the number of trials. p= the probability of a success on any one trial. 1 − p= the probability of a failure on any one trial. MATH 214 (NOTES) – p. 63/11 More about Binomial Distributions E(X) = µ = np V ar(X) = σ 2 = np(1 − p) MATH 214 (NOTES) – p. 64/11 Problem We are interested in estimating the average number of cars per household in a little town call Statstown. Let X represent the number of cars in a house picked at random. God knows that X has a Binomial distribution with n = 4 and p = 0.5. Suppose that we can only afford a sample of size 4 and that we are going to use this sample to estimate that population average. MATH 214 (NOTES) – p. 65/11 Problem (cont.) What we are going to do next is called a simulation. First, we will draw a lot of random samples coming from a Binomial Distribution with n = 4 and p = 0.5. Then we will make a histogram for all the x̄’s corresponding to our samples. We are going to do this to see what the histogram of x̄ looks like. This will give us an idea of what to expect in a similar situation. MATH 214 (NOTES) – p. 66/11 Sampling Distribution of x̄ 0.6 0.4 0.2 0.0 Density 0.8 1.0 Histogram of means 0 1 2 3 4 means MATH 214 (NOTES) – p. 67/11 Central Limit Theorem Draw a random sample of size n from any population with mean µ and finite standard deviation σ . When n is large, the sampling distribution of the sample mean x̄ is approximately Normal: (1) x̄ σ is approximately N (µ, √ ) n MATH 214 (NOTES) – p. 68/11 Example The number of accidents per week at a hazardous intersection varies with mean 2.2 and standard deviation 1.4. This distribution takes only whole-number values, so it is certainly not Normal. a) Let x̄ be the mean number of accidents per week at the intersection during a year (52 weeks). What is the approximate distribution of x̄ according to the central limit theorem? MATH 214 (NOTES) – p. 69/11 Example (cont.) b) What is the approximate probability that x̄ is less than 2? c) What is the approximate probability that there are fewer than 100 accidents at the intersection in a year? (Hint: Restate this event in terms of x̄) MATH 214 (NOTES) – p. 70/11 Solution a) By the Central Limit Theorem, x̄ is roughly Normal with = 0.1941. mean µ = 2.2 and standard deviation √σn = √1.4 52 b) P (x̄ < 2) = P ( x̄−µ < √σ n 2−2.2 0.1941 ) = P (Z < −1.0303) = 0.1515. c) Let xi be the number of accidents during week i. P52 P52 i=1 xi P (Total < 100) = P ( i=1 xi < 100) = P ( 52 < P (x̄ < 1.9230) = P (Z < −1.4270) = 0.0768 100 52 ) = MATH 214 (NOTES) – p. 71/11 Problem 18 (page 278) A population has a mean of 200 and a standard deviation of 50. A simple random sample of size 100 will be taken and the sample mean x̄ will be used to estimate the population mean. a. What is the expected value of x̄. b. What is the standard deviation of x̄. c. Show the sample distribution of x̄. MATH 214 (NOTES) – p. 72/11 Solution a. E(x̄) = µ = 200. =5 b. σx̄ = √σn = √50 100 c. By the Central Limit Theorem, x̄ is roughly Normal with mean µ = 200 and standard deviation √σn = 5. MATH 214 (NOTES) – p. 73/11 Problem 19 (page 278) A population has a mean of 200 and a standard deviation of 50. Suppose a simple random sample of size 100 is selected and x̄ is used to estimate µ. a. What is the probability that the sample mean will be within ±5 of the population mean? b. What is the probability that the sample mean will be within ±10 of the population mean? MATH 214 (NOTES) – p. 74/11 Solution By the Central Limit Theorem, x̄ is roughly Normal with mean µ = 200 and standard deviation √σn = 5. a. P (195 ≤ x̄ ≤ 205) = P ( 195−200 ≤ 5 x̄−µ √σ n ≤ 205−200 ) 5 = P (−1 ≤ Z ≤ 1) = P (Z ≤ 1) − P (Z ≤ −1) = 0.8413 − 0.1587 = 0.6826 x̄−µ 210−200 ≤ b. P (190 ≤ x̄ ≤ 210) = P ( 190−200 ≤ )= σ √ 5 5 n P (−2 ≤ Z ≤ 2) = P (Z ≤ 2) − P (Z ≤ −2) = 0.9772 − 0.0228 = 0.9544 MATH 214 (NOTES) – p. 75/11 Problem 24 The mean tuition cost at state universities throughout the United States is $ 4260 per year . Use this value as the population mean and assume that the population standard deviation is σ = $900. Suppose that a random sample of 50 state universities will be selected. a. Show the sampling distribution of x̄ where x̄ is the sample mean tuition cost for the 50 state universities. b. What is the probability that the simple random sample will provide a sample mean within $250 of the population mean? c. What is the probability that the simple random sample will provide a sample mean within $100 of the population mean? MATH 214 (NOTES) – p. 76/11 Solution a. By the Central Limit Theorem, x̄ has roughly a N (µ, √σn ). In this case, x̄ has roughly a N (4260, √900 ), that is, x̄ has 50 roughly a N (4260, 127.28) 4510−4260 b. P (4010 ≤ x̄ ≤ 4510) = P ( 4010−4260 ≤ Z ≤ 127.28 127.28 ) = P (−1.96 ≤ Z ≤ 1.96) = 0.9750 − 0.025 = 0.95 4360−4260 ≤ Z ≤ c. P (4160 ≤ x̄ ≤ 4360) = P ( 4160−4260 127.28 127.28 ) = P (−0.79 ≤ Z ≤ 0.79) = 0.7852 − 0.2148 = 0.5704 MATH 214 (NOTES) – p. 77/11 Problem 25 The College Board College Testing Program reported a population mean SAT score of µ = 1020. Assume that the population standard deviation is σ = 100. a. What is the probability that a random sample of 75 students will provide a sample mean SAT score within 10 of the population mean? b. What is the probability a random sample of 75 students will provide a sample mean SAT score within 20 of the population mean? MATH 214 (NOTES) – p. 78/11 CHAPTER 8 INTERVAL ESTIMATION MATH 214 (NOTES) – p. 79/11 M & M’s If you buy an 8 pack of m & m’s fun size you will find the following information: Nutrition Facts Serving Size 3 packs (45 g) Which implies that: 1 pack = 15 g, right?. Since we are buying an 8 pack the net weight should be (8)(15) = 120 g, right?. However, the net weight on the label is 117.1 g, How can we explain that?. MATH 214 (NOTES) – p. 80/11 Interval Estimate of a Population Mean:σ kn σ x̄ ± z∗ ( √ ) n where z∗ is a number coming from a Standard Normal that depends on the confidence level required. MATH 214 (NOTES) – p. 81/11 Problem 1 A simple random sample of 40 items resulted in a sample mean of 25. The population standard deviation is σ = 5. a. What is the standard error of the mean, σx̄ ? b. At 95% confidence, what is the margin of error? MATH 214 (NOTES) – p. 82/11 Solution a. standard error of the mean = σx̄ = √σn = √540 = 0.7905 b. margin of error = z∗ √σn = (1.96)(0.7905) = 1.5493 MATH 214 (NOTES) – p. 83/11 Problem 2 (page 306) A simple random sample of 50 items from a population with σ = 6 resulted in a sample mean of 32. a. Provide a 90% confidence interval for the population mean? b. Provide a 95% confidence interval for the population mean? c. Provide a 99% confidence interval for the population mean? MATH 214 (NOTES) – p. 84/11 Solution a. x̄ = 32, σ = 6, n = 50 and z∗ = 1.65 (x̄ − z∗ √σn , x̄ − z∗ √σn ) (32 − 1.65( √650 ), 32 − 1.65( √650 )) (30.5999, 33.4000) 90% Confidence Interval for µ. b. (32 − 1.96( √650 ), 32 − 1.96( √650 )) (30.3368, 33.6631) 95% Confidence Interval for µ. MATH 214 (NOTES) – p. 85/11 Problem 5 (page 306) In an effort to estimate the mean amount spent per customer for dinner at a major Atlanta restaurant, data were collected for a sample of 49 customers. Assume a population standard deviation of $ 5. a. At 95% confidence, what is the margin of error? b. If the sample mean is $ 24.80, what is the 95% confidence interval for the population mean? MATH 214 (NOTES) – p. 86/11 Solution In this case, µ = mean amount spent per customer for dinner for all customers at a major Atlanta restaurant. a. margin of error = z∗ ( √σn ) = 1.96( √549 ) = 1.4 b. (x̄ − z∗ √σn , x̄ − z∗ √σn ) (24.80 − 1.4, 24.80 + 1.4)) (23.40, 26.20) 95 % Confidence Interval for µ. MATH 214 (NOTES) – p. 87/11 Problem 10 (page 306) Playbill magazine reported that the mean annual household income of its readers is $ 119,155. Assume this estimate of the mean annual household income is based on a sample of 80 households, and based on past studies, the population standard deviation is known to be σ = $ 30,000. a. Develop a 90 % confidence interval estimate of the population mean. b. Develop a 95 % confidence interval estimate of the population mean. c. Develop a 99 % confidence interval estimate of the population mean. MATH 214 (NOTES) – p. 88/11 Solution a. (x̄ − z∗ √σn , x̄ − z∗ √σn ) 30,000 √ √ ), 119, 155 − 1.65( (119, 155 − 1.65( 30,000 )) 80 80 (113, 620.73; 124, 689.26) 90% Confidence Interval for µ. 30,000 √ √ ), 119, 155 − 1.96( )) b. (119, 155 − 1.96( 30,000 80 80 (112, 580.96; 125, 729.03) 95% Confidence Interval for µ. 30,000 √ √ c. (119, 155 − 2.58( 30,000 )) ), 119, 155 − 2.58( 80 80 (110501.41; 127808.58) 99% Confidence Interval for µ. MATH 214 (NOTES) – p. 89/11 Problem 11 (page 314) For a t distribution with 16 degrees of freedom, find the area, or probability, in each region. a. To the right of 2.120. b. To the left of 1.337. c. To the left of -1.746. d. To the right of 2.583. e. Between -2.120 and 2.120. f. Between -1.746 and 1.746. MATH 214 (NOTES) – p. 90/11 Solution (Go to page 920) Let T represent a t distribution with 16 degrees of freedom. a. P (T > 2.120) = 0.025. b. P (T < 1.337) = 0.10. c. P (T < −1.746) = P (T > 1.746) = 0.05. (Because t distributions are symmetric). d. P (T > 2.583) = 0.01. e. P (−2.120 < T < 2.120) = 0.95. f. P (−1.746 < T < 1.746) = 0.90. MATH 214 (NOTES) – p. 91/11 Problem 12 (page 314) Find the t value(s) for each of the following cases. a. Upper tail area of 0.025 with 12 degrees of freedom. b. Lower tail area of 0.05 with 50 degrees of freedom. c. Upper tail area of 0.01 with 30 degrees of freedom. d. Where 90 % of the area falls between these two t values with 25 degrees of freedom? e. Where 95 % of the area falls between these two t values with 45 degrees of freedom? MATH 214 (NOTES) – p. 92/11 Solution a. t∗ = 2.179. (TI-84: invT(0.975,12)= 2.1788). b. t∗ = −1.676 (TI-84: invT(0.05,50)= -1.6759). c. t∗ = 2.457 (TI-84: invT(0.99,30)= 2.4572). d. t∗ = 2.014 (TI-84: invT(0.975,45)= 2.014). e. t∗ = 1.708 (TI-84: invT(0.99,30)= 2.4572). MATH 214 (NOTES) – p. 93/11 Problem 13 (page 314) The following sample data are from a normal population: 10, 8, 12, 15, 13, 11, 6, 5. a. What is the point estimate of the population mean? b. What is the point estimate of the population standard deviation? c. With 95 % confidence, what is the margin of error for the estimation of the population mean? d. What is the 95 % confidence interval for the population mean? MATH 214 (NOTES) – p. 94/11 Solution a. x̄ = 10. b. s = 3.4641. √ ) = 2.8965. c. margin of error = t∗ √sn = 2.365( 3.4641 8 d. (x̄ − t∗ ( √sn ), x̄ + t∗ ( √sn )) (7.1039, 12.896) (using a TI-84). MATH 214 (NOTES) – p. 95/11 Problem 14 (page 314) A simple random sample with n = 54 provided a sample mean of 22.5 and a sample standard deviation of 4.4. a. Develop a 90% confidence interval for the population mean. b. Develop a 95% confidence interval for the population mean. c. Develop a 99% confidence interval for the population mean. MATH 214 (NOTES) – p. 96/11 Solution a. (x̄ − t∗ ( √sn ), x̄ + t∗ ( √sn )) 4.4 √ (22.5 − 1.674( √4.4 ), 22.5 + 1.674( )) 54 54 (21.498, 23.502). (using a TI-84) 4.4 √ b. (22.5 − 2.006( √4.4 )) ), 22.5 + 2.006( 54 54 (21.299, 23.701) (using a TI-84) 4.4 √ c. (22.5 − 2.672( √4.4 ), 22.5 + 2.672( )) 54 54 (20.9, 24.1) (using a TI-84) MATH 214 (NOTES) – p. 97/11 Problem 15 (page 315) Sales personnel for Skillings Distributors submit weekly reports listing the customer contacts made during the week. A sample of 65 weekly reports showed a sample mean of 19.5 customer contacts per week. The sample standard deviation was 5.2. Provide a 90% and 95% confidence intervals for the population mean number of weekly customer contacts for the sales personnel. MATH 214 (NOTES) – p. 98/11 Solution 90 % Confidence. (x̄ − t∗ ( √sn ), x̄ + t∗ ( √sn )) 5.2 √ ), 19.5 + 1.669( )) (19.5 − 1.669( √5.2 65 65 (18.42, 20.58) 95 % Confidence. (x̄ − t∗ ( √sn ), x̄ + t∗ ( √sn )) 5.2 √ (19.5 − 1.998( √5.2 ), 19.5 + 1.998( )) 65 65 (18.21, 20.79) MATH 214 (NOTES) – p. 99/11 Problem 23 (page 318) How large a sample should be selected to provide a 95% confidence interval with a margin of error of 10? Assume that the population standard deviation is 40. MATH 214 (NOTES) – p. 100/11 Problem 24 (page 318) The range for a set of data is estimated to be 36. a. What is the planning value for the population standard deviation? b. At 95% confidence, how large a sample would provide a margin of error of 3? c. At 95% confidence, how large a sample would provide a margin of error of 2? MATH 214 (NOTES) – p. 101/11 Problem 25 (page 318) Scheer Industries is considering a new computer-assisted program to train maintenance employees to do machine repairs. In order to fully evaluate the program, the director of manufacturing requested an estimate of the population mean time required for maintenance employees to complete the computer-assisted training. Use 6.84 days as a planning value for the population standard deviation. a. Assuming 95% confidence, what sample size would be required to obtain a margin of error of 1.5 days? b. If the precision statement was made with 90% confidence, what sample size would be required to obtain a margin of error of 2 days? MATH 214 (NOTES) – p. 102/11 Problem 28 (page 318) Smith Travel Research provides information on the one-night cost of hotel rooms through-out the United States. Use $ 2 as the desired margin of error and $ 22.50 as the planning value for the population standard deviation to find the sample size recommended in a), b), and c). a. A 90% confidence interval estimate of the population mean cost of hotel rooms. b. A 95% confidence interval estimate of the population mean cost of hotel rooms. c. A 99% confidence interval estimate of the population mean cost of hotel rooms. MATH 214 (NOTES) – p. 103/11 Problem A market research consultant hired by the Pepsi-Cola Co. is interested in determining the proportion of IUP students who favor Pepsi-Cola over Coke Classic. A random sample of 100 students shows that 40 students favor Pepsi over Coke. Use this information to construct a 95% confidence interval for the proportion of all students in this market who prefer Pepsi. MATH 214 (NOTES) – p. 104/11 Bernoulli Distribution xi = ( 1 i-th person prefers Pepsi 0 i-th person prefers Coke µ = E(xi ) = p σ 2 = V (xi ) = p(1 − p) Pn xi Let p̂ be our estimate of p. Note that p̂ = n = x̄. If n is "large", by the Central Limit Theorem, we know that: x̄ is roughly N (µ, √σn ), that is, i=1 q p̂ is roughly N p, p(1−p) n MATH 214 (NOTES) – p. 105/11 Problem 31 (page 322) A simple random sample of 400 individuals provides 100 Yes responses. a. What is the point estimate of the proportion of the population that would provide Yes responses? b. What is the point estimate of the standard error of the proportion, σp̂ ? c. Compute the 95% confidence interval for the population proportion. MATH 214 (NOTES) – p. 106/11 Problem 32 (page 323) A simple random sample of 800 elements generates a sample proportion p̂ = 0.70. a. Provide a 90% confidence interval for the population proportion. b. Provide a 95% confidence interval for the population proportion. MATH 214 (NOTES) – p. 107/11 Problem 35 (page 323) A survey of 611 office workers investigated telephone answering practices, including how often each office worker was able to answer incoming telephone calls and how often incoming telephone calls went directly to voice mail. A total of 281 office workers indicated that they never need voice mail and are able to take every telephone call. a. What is the point estimate of the proportion of the population of office workers who are able to take every telephone call? b. At 90% confidence, what is the margin of error? c. What is the 90% confidence interval for the proportion of the population of office workers who are able to take every telephone call? MATH 214 (NOTES) – p. 108/11 Problem 33 (page 323) In a survey, the planning value for the population proportion is p∗ = 0.35. How large a sample should be taken to provide a 95% confidence interval with a margin of error of 0.05? MATH 214 (NOTES) – p. 109/11 Problem 34 (page 323) At 95% confidence, how large a sample should be taken to obtain a margin of error of 0.03 for the estimation of a population proportion? Assume that past data are not available for developing a planning value for p∗ . MATH 214 (NOTES) – p. 110/11 TO BE CONTINUED... MATH 214 (NOTES) – p. 111/11