* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download lies opposite the longest side
History of geometry wikipedia , lookup
Golden ratio wikipedia , lookup
Euler angles wikipedia , lookup
Riemann–Roch theorem wikipedia , lookup
Four color theorem wikipedia , lookup
Noether's theorem wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Brouwer fixed-point theorem wikipedia , lookup
Rational trigonometry wikipedia , lookup
Euclidean geometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
Incircle and excircles of a triangle wikipedia , lookup
History of trigonometry wikipedia , lookup
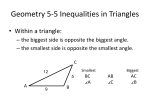
LESSON 5-5 INEQUALITIES IN TRIANGLES OBJECTIVE: To use inequalities involving angles and sides of triangles Theorem 5-10 If a triangle is scalene, then the largest angle lies opposite the longest side and the smallest angle lies opposite the shortest side. X Example 1: List the angles from smallest to largest Z Y X 17” Y 29” 32” Z Theorem 5-11(Converse of Theorem 5-10) If a triangle is scalene, then the longest side lies opposite the largest angle, and the shortest side lies opposite the smallest angle. Example 2: In QRS, list the sides from smallest to largest SR QS QR Q 30° S R Example 3: In TUV, which side is the shortest? Use sum to find mT. mT = 60°, so U is smallest T Therefore VT is shortest U 58° 62° V Theorem 5-12 The Triangle Inequality Theorem The sum of the lengths of any two sides of a triangle is greater than the length of the third side. Example 4: Can a triangle have sides with the given lengths? Explain. b) 3cm., 6cm., 10cm. a) 3ft., 7ft., 8ft. Yes, 3 + 7 > 8 NO, 3 + 6 < 10 Example 5: A triangle has sides of lengths 8cm and 10cm. Describe the lengths possible for the third side. Let x = the length of the 3rd side. The sum of any 2 sides must be greater than the 3rd. So, there are 3 possibilities. x + 8 > 10 x>2 x + 10 > 8 x > -2 8 + 10 > x 18 > x x < 18 So, x must be longer than 2cm & shorter than 18cm. 2 < x < 18 ASSIGNMENT: Page 277 #4-25, 34-36, 43-46