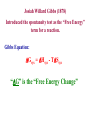* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Entropy and Free Energy
Heat transfer physics wikipedia , lookup
Conservation of energy wikipedia , lookup
Adiabatic process wikipedia , lookup
Internal energy wikipedia , lookup
Non-equilibrium thermodynamics wikipedia , lookup
History of thermodynamics wikipedia , lookup
Thermodynamic system wikipedia , lookup
Second law of thermodynamics wikipedia , lookup
Maximum entropy thermodynamics wikipedia , lookup
Entropy in thermodynamics and information theory wikipedia , lookup
Gibbs free energy wikipedia , lookup
Entropy and Free Energy The Basis for Thermodynamics First law of thermodynamics: The change in the energy of a system ∆U = q + w is the sum of the heat and the work done by or on the system. the first law does not, however, account for the observation that natural processes have a direction of progress. q ∆S T Second Law of Thermodynamics: The Second Law of Thermodynamics states that the state of entropy of the entire universe, as a closed isolated system, will always increase over duration. Entropy always increases in the direction of duration. The second law also states that the changes in the entropy in the universe can never be negative Spontaneous Physical and Chemical Processes • A waterfall runs downhill • A lump of sugar dissolves in a cup of coffee • At 1 atm, water freezes below 0 0C and ice melts above 0 0C • Heat flows from a hotter object to a colder object • A gas expands in an evacuated bulb • Iron exposed to oxygen and water forms rust spontaneous nonspontaneous 18.2 spontaneous nonspontaneous 18.2 Entropy (S): A measure of the degrees of freedom of the system. (A measure of the disorder of the system.) Second Law of Thermodynamics: All processes occur spontaneously in the direction that increases the entropy of the universe. ∆Suniv = ∆Ssys+ ∆Ssurr > 0 k – Boltzmann constant 1.38 x 10-23 J/K R/NA S = k ln W W – ways of arranging the components of a system without changing its energy. (microstates) Third Law of Thermodynamics: A perfect crystal has zero entropy at a temperature of absolute zero. Random Motion in a Crystal [Not at 0 K] ∆Suniv = 0 at 0 K Richard Feynman on Entropy : “So we now have to talk about what we mean by disorder and what we mean by order. ... Suppose we divide the space into little volume elements. If we have black and white molecules, how many ways could we distribute them among the volume elements so that white is on one side and black is on the other? On the other hand, how many ways could we distribute them with no restriction on which goes where? Clearly, there are many more ways to arrange them in the latter case. We measure "disorder" by the number of ways that the insides can be arranged, so that from the outside it looks the same. The logarithm of that number of ways is the entropy. The number of ways in the separated case is less, so the entropy is less, or the "disorder" is less.” Adding energy to a system always changes the entropy of the system. The definition of entropy derived from the second law of thermodynamics has no molecular interpretation. The Austrian physicist Ludwig Boltzmann (1844-1907) showed in 1877 that entropy has a fundamental molecular significance: It is a measure of the disorder of a system. This disorder can be asymmetry or displacement. This significance is relevant in the sub-atomic nature of the physical universe as well. Boltzmann proposed that entropy is related to the number of different microscopic views of obtaining a specified macroscopically definable and observable situation. If the number of equivalent ways of constructing a system is W, then the entropy is proportional to the logarithm of W: “In the admission of synthetic expertise among chemists, it is embarrassingly admitted also that it is impossible to re-create even the simplest enzyme or structural protein found in biotic materials. The process that requires entropy reduction to increase complexity also requires heat energy to form chemical bonds. This produces an obstacle for our un-hindered production of amazingly complex molecules.” Pharmaceuticals, polymers, enzymes and structural and nutrient proteins all require the original biotic material to begin with, as it contains an entropy reducing structure: catalysts and replication directing chemical structures containing information (RNA,DNA) as well as sophisticated electronic energy work. The smallest DNA/RNA strand contains more information than the whole of the Encyclopedia Britannica Information is capable of reducing entropy-but information is also susceptible to entropy. An example is the polymerization of amino acids to form protenoids: a Amino acid A + b Amino acid B c polymer + d H2O La Chateliers principle indicates that this equilibrium would lie far to the left and entropy requirements will grow rapidly with molecular weight. Some small protenoids have been formed in the laboratory, but they are small molecular weight species. The free energy to incorporate many high M.W. amino acids into larger polymers has a limiting factor we shall derive later. Binomial Distribution Only four states Are solid crystals The rest are gases Counter examples exist: A new state function can be defined, the free energy, G: G = H - TS For reactions at constant temperature and pressure, any reaction is spontaneous when G decreases. In a reversible process in which no external work is involved the free energy of a reacting system does not change and G=0. If the system does electric, magnetic or gravitational work then: where all other work is wext so that: When a system does work on its surroundings in a reversible way, the decrease In the free energy exactly balances the work done other than pressure-volume Work. Thermodynamics State functions are properties that are determined by the state of the system, regardless of how that condition was achieved. energy, enthalpy, pressure, volume, temperature, entropy. Potential energy of hiker 1 and hiker 2 is the same even though they took different paths. 6.7 Entropy Changes in the System (∆Ssys) The standard entropy of reaction (∆S0 ) is the entropy change for a reaction carried out at rxn 1 atm and 250C. aA + bB ∆S0 [ = rxn ∆S0 rxn cS0(C) + = Σ nS0(products) cC + dD dS0(D) ] - [ aS0(A) + bS0(B) ] - Σ mS0(reactants) What is the standard entropy change for the following reaction at 250C? 2CO2 (g) 2CO (g) + O2 (g) S0(CO) = 197.9 J/K•mol S0(CO2) = 213.6 J/K•mol S0(O2) = 205.0 J/K•mol ∆S0 ∆S0 rxn rxn = 2 x S0(CO2) – [2 x S0(CO) + S0 (O2)] = 427.2 – [395.8 + 205.0] = -173.6 J/K•mol 18.3 3 Factors Involved in Determining Whether a Reaction is Spontaneous or Not ∆H; a negative value (exothermic reactions) favors a spontaneous reaction ∆S; a positive value (disorder increases) favors a spontaneous reaction Temperature; If the above factors conflict; temperature determines if reaction is spontaneous or not ∆S -∆H +∆S Spontaneous at all Temperatures ∆G=∆H-T∆S +∆H +∆S Spontaneous at High Temperatures ∆H -∆H -∆S Spontaneous at Low Temperatures +∆H -∆S NonSpontaneous at all Temperatures Conditions for Spontaneity of a Reaction ∆S osurroundings = - Recall: ∆H osystem T ∆Suniv = ∆Ssys + ∆Ssurr > 0 Josiah Willard Gibbs (1878) Introduced the spontaneity test as the “Free Energy” term for a reaction. Gibbs Equation: ∆Gsys = ∆Hsys - T∆Ssys “∆G” is the “Free Energy Change” Gibbs Free Energy and Spontaneity ∆G < 0 Spontaneous ∆G > 0 Nonspontaneous ∆G = 0 Equilibrium The value of ∆G indicates the amount of energy which is available to do useful work! Gibbs Free Energy For a constant-temperature process: Gibbs free energy (G) ∆G = ∆Hsys -T∆Ssys ∆G < 0 The reaction is spontaneous in the forward direction. ∆G > 0 The reaction is nonspontaneous as written. The reaction is spontaneous in the reverse direction. ∆G = 0 The reaction is at equilibrium. 18.4 ∆G; Change in Gibb’s Free Energy ∆G = ∆Hsys -T∆Ssys 1. Determine if reaction is spontaneous or not. 2. wmax; free energy available to do useful work. ∆G = wmaximum ∆Hsys; represents energy available for useful work -T∆Ssys; represents energy that can’t Be harnessed to do useful work Ways to Obtain ∆Greaction 1. From ∆Gfo Values 2. From Gibb’s Free Energy Equation ∆G = ∆Hsys -T∆Ssys The standard free-energy of reaction (∆G0 ) is the free-energy change for a reaction rxn when it occurs under standard-state conditions. aA + bB ∆G0 ∆G0 rxn = [ c∆G0 (C) + f = Σ n∆G0 (products) rxn f d∆G0 (D) ] - [ f cC + dD a∆G0 (A) + f b∆G0 (B) ] f - Σ m∆G0 (reactants) f Standard free energy of formation (∆G0) is the free-energy change that occurs when 1 mole of the f compound is formed from its elements in their standard states. ∆G0 of any element in its stable form is zero. f 18.4 What is the standard free-energy change for the following reaction at 25 0C? 2C6H6 (l) + 15O2 (g) ∆G0 ∆G0 ∆G0 rxn rxn 12CO2 (g) + 6H2O (l) = Σ n∆G0 (products) rxn f 12∆G0 (CO2) + f - Σ m∆G0 (reactants) f 6∆G0 (H2O)] - [ f = [ = [ 12x–394.4 + 6x–237.2 ] – [ 2x124.5 ] = -6405 kJ 2∆G0 (C6H6)] f Is the reaction spontaneous at 25 0C? ∆G0 = -6405 kJ <0 spontaneous 18.4 Temperature and Spontaneity of Chemical Reactions CaCO3 (s) CaO (s) + CO2 (g) ∆H0 = 177.8 kJ; Does not favor spontaneous reaction ∆S0 = 160.5 J/K; Favors spontaneous reaction ∆G0 = ∆H0 – T∆S0 Determine the temperature range where the above reaction will be spontaneous. -∆G; spontaneous ∆G=0;equilibrium +∆G;nonspontaneous 0 = ∆H0 – T∆S0 ∆H0 = T∆S0 T=∆Η0/ ∆S0 T = 177.8 kJ/ 0.1605 kJ/K =1108K Entropy and States of Matter [Note entropy and temperature changes.] Predicting Relative Standard Molar Entropy Values [So] of a System 1 atm 1M 298 K (25oC) Most Stable Form for Solids or Liquids Fig. 20.5 Gibbs Free Energy and Phase Transitions Ice melting; Liquid vaporizing Solid subliming H2O (l) H2O (g) Phase changes happen at equilibrium ∆G0 = ∆H0 – T∆S0 ∆G0 = 0 T=∆H0/ ∆S0 Determine the boiling point of water given that ∆Svap = 109.3 J/mole K and ∆Hvap = 40.62 kJ/mole. T = 40.6 kJ/mole = 373 K = 100 °C 0.1093 kJ/mole K 18.4