Download Lecture Notes 2

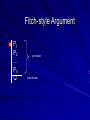
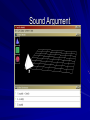
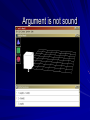
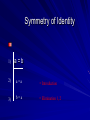
CS1502 Formal Methods in
Computer Science
Lecture Notes 2
Introduction to Logic
Part 2
What is an argument?
A series of statements in which one
(called the conclusion) is meant to follow
from the others (called the premises).
Not talking about the *&^%$% type of
argument
Fitch-style Argument
P1
P2
...
Pn
Q
premises
conclusion
Valid Argument
A valid argument is one that guarantees
the truth of its conclusion on the
assumption that the premises are true.
A valid argument ensures the conclusion
is true provided the premises are true.
Often written premises |= conclusion
Valid Argument - Example
•
Large(b) v Cube(b)
Cube(b)
Large(b)
premises
Large(b)
T
T
F
F
Cube(b)
T
F
T
F
Large(b) v Cube(b)
T
T
T
F
conclusion
 Cube(b)
F
T
F
T
Large(b)
T
T
F
F
Sound Argument
If an argument is valid and its premises
are true, then the argument is said to be
sound.
Sound Argument
Argument is not sound
Examples
Which are valid? Sound?
(worked out in lecture)
All men are mortal. Socrates is a man. So,
Socrates is Mortal.
Bill is a man. After all, Bill is mortal and all men
are mortal.
All women are taller than all men. Ralph is a
woman and Bill is a man. Therefore, Ralph is
taller than Bill.
Examples
Which are valid? Sound?
Since this class meets Tuesday after
12:45pm, it is January.
Tom Hanks is a good actor. After all, all rich
actors are good actors, and Tom Hanks is
a rich actor.
Methods of Proof
Formal: We will use a Fitch-style proof
employed in the software.
Informal: This style of proof, used by
mathematicians, is just as rigorous. It consists
of sentences describing the situation at hand,
the inferences being made, and the
justification of each inference.
Difference? The amount of explicit detail.
What constitutes a proof?
Proof that P1,P2,…,Pn |= Q is:
a step-by-step demonstration showing
that Q must be true in any circumstances
in which all of P1,P2,…,Pn are true.
Fitch-style Proof
P1
P2
…
Pn
S1
S2
…
Sn
Q
Premises
Deductions & Justifications
may contain sub-proofs
Conclusion
Proof Rules
Proof rules are used to construct proofs (both
formal and informal)
That is, each step but the premises has to be
justified by a proof rule
As we introduce more pieces of FOL, we will
introduce more proof rules
We’ll start now with proof rules involving identity
=
Rules
= Elimination
If b = c and P(b) then P(c).
= Introduction
a=a
Symmetry of Identity
If a = b then b = a.
Transitivity of Identity
If a = b and b = c then a = c
These follow from above
= Elimination
P(n)
n=m
P(m)
= Introduction
n=n
Symmetry of Identity
1)
a=b
2)
a=a
= Introduction
3)
b=a
= Elimination 1, 2
Example Formal Proof
1)
2)
Larger(a,b)
c=b
3) Smaller(b,a)
Ana Con 1
4)
c=c
= Introduction
5)
b=c
= Elim 2, 4
6)
Smaller(c,a)
= Elim 5, 3
Explicit Proof of Ana Con step
This is a look ahead – we haven’t seen these proof rules before.
Note: As this is displaying, the line is in the wrong place. It should be
between lines 2 and 3.
Example Informal Proof
Prove: If a is smaller than b and c is identical to b
then c is larger than a.
Since we are given that a is smaller than b, it follows
that b must be larger than a. Moreover, since c is
identical to b, it follows that c must be larger than a.
QED