* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
History of genetic engineering wikipedia , lookup
Heritability of IQ wikipedia , lookup
Public health genomics wikipedia , lookup
Genetic engineering wikipedia , lookup
Genome (book) wikipedia , lookup
Human genetic variation wikipedia , lookup
Genetic testing wikipedia , lookup
Koinophilia wikipedia , lookup
Genetic drift wikipedia , lookup
Computational phylogenetics wikipedia , lookup
Microevolution wikipedia , lookup
What is Genetic Programming?
• Genetic programming is a model of programming which
uses the ideas (and some of the terminology) of biological
evolution to handle a complex problem. … Genetic
programming can be viewed as an extension of the genetic
algorithm, a model for testing and selecting the best choice
among a set of results, each represented by a string.
Definition: Genetic Programming
•
•
•
•
One of the central problems in computer science is how to make
computers solve problems without being explicitly programmed
to do so.
Genetic programming offers a solution through the evolution of
computer programs by methods of natural selection.
Genetic programming is a recent development in the area of
evolutionary computation. It was greatly stimulated in the 1990s
by John Koza.
According to Koza, genetic programming searches the space of
possible computer programs for a program that is highly fit for
solving the problem at hand.
Outline of the Genetic Algorithm
• Randomly generate a set of possible solutions to a problem,
representing each as a fixed length character string
• Test each possible solution against the problem using a
fitness function to evaluate each solution
• Keep the best solutions, and use them to generate new
possible solutions
• Repeat the previous two steps until either an acceptable
solution is found, or until the algorithm has iterated
through a given number of cycles (generations)
GA flowchart
GP flowchart
Why Genetic Programming?
• “It is difficult, unnatural, and overly restrictive to
attempt to represent hierarchies of dynamically
varying size and shape with fixed length character
strings.” “For many problems in machine learning
and artificial intelligence, the most natural
representation for a solution is a computer
program.” [Koza, 1994]
• A parse tree is a good representation of a
computer program for Genetic Programming
Using Trees To Represent
Computer Programs
(+ 2 3 (* X 7) (/ Y 5))
Functions
+
2
3
*
X
Terminals
/
7
Y
5
Genetic Operations
• Random Generation of the initial population
of possible solutions
• Mutation of promising solutions to create
new possible solutions
• Genetic Crossover of two promising
solutions to create new possible solutions
Randomly Generating Programs
• Randomly generate a program that takes two arguments
and uses basic arithmetic to return an answer
– Function set = {+, -, *, /}
– Terminal set = {integers, X, Y}
• Randomly select either a function or a terminal to represent
our program
• If a function was selected, recursively generate random
programs to act as arguments
Initialisation
• Maximum initial depth of trees Dmax is set
• Full method (each branch has depth = Dmax):
– nodes at depth d < Dmax randomly chosen from function set F
– nodes at depth d = Dmax randomly chosen from terminal set T
• Grow method (each branch has depth Dmax):
– nodes at depth d < Dmax randomly chosen from F T
– nodes at depth d = Dmax randomly chosen from T
• Common GP initialisation: ramped half-and-half, where
grow & full method each deliver half of initial population
Full Method
Grow Method
Randomly Generating Programs
(+ …)
+
Randomly Generating Programs
(+ 2 …)
+
2
Randomly Generating Programs
(+ 2 3 …)
+
2
3
Randomly Generating Programs
(+ 2 3 (* …) …)
+
2
3
*
Randomly Generating Programs
(+ 2 3 (* X 7) (/ …))
+
2
3
*
X
/
7
Randomly Generating Programs
(+ 2 3 (* X 7) (/ Y 5))
+
2
3
*
X
/
7
Y
5
Selection
• Fitness-proportional Selection
– all individuals have a chance of being selected
at any given point.
– the probability that a given individual will be
selected is equal to its normalized fitness
• Tournament Selection
– selecting a number of individuals from the
population at random, a tournament, and then
selecting only the best of those individuals.
Codes for Fitness-Proportional
Selction
Codes for Tournament Selection
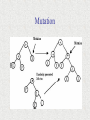
Mutation
• Most common mutation: replace randomly
chosen subtree by randomly generated tree
– A function node could for example change its
function type or turn into a terminal node.
– A terminal node representing a variable could
for example change its index and thus in the
following refer to another variable.
– A terminal node representing a constant could
be multiplied with a factor.
Mutation
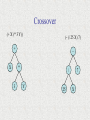
Crossover/Recombination
• Most common recombination: exchange
two randomly chosen subtrees among the
parents
• Recombination has two parameters:
– Probability to chose an internal point within
each parent as crossover point
– Two-point crossover
• The size of offspring can exceed that of the
parents
Crossover
(+ X (* 3 Y))
(- (/ 25 X) 7)
+
-
X
*
3
/
Y
25
7
X
Crossover
(+ X (* 3 Y))
Pick a random node in
each program
+
X
(- (/ 25 X) 7)
-
*
3
/
Y
25
7
X
Crossover
(+ X (* (/ 25 X) Y))
Swap the two nodes
+
X
*
/
25
(- 3 7)
3
Y
X
-
7
Crossover (Conti.)
• One-point crossover
– First the two parent trees are traversed to
identify the parts with the same shape, i.e. with
the same arity in the nodes encountered
traversing the tree from the roots node.
– A random crossover point is selected with a
uniform probability among the links belonging
to the common parts identified in the previous
step.
• An important consequences of the convergence property of
GP with one-point crossover is that like in GAs mutation
becomes a very important operator to prevent premature
convergence and to maintain diversity.
Fitness
• The fitness measure is the way we define
the problem to GP.
• The fitness function determines how well a
program is able to solve the problem.
– Mean squared errors function (MSE)
– Coefficient of determination
– Variance accounted for function
Symbolic Regression Problem
• The following Java code shows how the raw
fitness can be calculated for the symbolic
regression problem:
Bloat
• Bloat = “survival of the fattest”, i.e., the tree
sizes in the population are increasing over
time
• Ongoing research and debate about the
reasons
• Needs countermeasures, e.g.
– Prohibiting variation operators that would
deliver “too big” children
– Parsimony pressure: penalty for being
oversized
Controlling Bloat
• Depth limitation for the generation of
individuals in the initial population.
• Depth limitation for the generation of subtrees for sub-trees mutation and crossover
operators.
• Pruning and planting a sub-tree
– The worst tree in a population will be
substituted by branches pruned from one of the
best tree and planted in its place.
Another Examples for Pruning
Problems involving “physical”
environments
• Trees for data fitting vs. trees (programs) that are “really”
executable
• Execution can change the environment the calculation
of fitness
• Example: robot controller
• Fitness calculations mostly by simulation, ranging from
expensive to extremely expensive (in time)
• But evolved controllers are often to very good
What About Just Randomly
Generating Programs?
• Is Genetic Programming really better than just randomly
creating new functions?
• Yes!
– Pete Angeline compared the result of evolving a tic-tac-toe
algorithm for 200 generations, with a population size of 1000 per
generation, against 200,000 randomly generated algorithms
– The best evolved program was found to be significantly superior to
the best randomly generated program [Genetic Programming FAQ,
2002]
• The key lies in using a fitness measure to determine which
functions survive to reproduce in each generation
END~