Download Significant Figures and Scientific Notation for Chem Tech and Chem

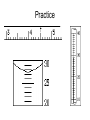
Significan Digits
aka
Significant Figures
What are they?
They show the certainty (precision) of your measuring
device.
0.1g
0.1000g
What’s the difference in these two numbers?
*Sig. Figs. are only for measurements. So always ask, is
the value you are looking at a measurement of some
kind. The sig. figs. for exact values are ignored.
*The last digit is always the digit that is least certain (the
digit you are estimating).
More Difficult Rules
(1) All nonzero digits are significant:
1.234 g has 4 significant figures,
1.2 g has 2 significant figures.
(2) Zeroes between nonzero digits are significant:
1002 kg has 4 significant figures,
3.07 mL has 3 significant figures.
(3) Leading zeros to the left of the first nonzero digits are not significant; such zeroes merely indicate the position of the
decimal point:
o
0.001 C has only 1 significant figure,
0.012 g has 2 significant figures.
(4) Trailing zeroes that are also to the right of a decimal point in a number are significant:
0.0230 mL has 3 significant figures,
0.20 g has 2 significant figures.
(5) When a number ends in zeroes that are not to the right of a decimal point, the zeroes are not necessarily significant:
190 miles may be 2 or 3 significant figures,
50,600 calories may be 3, 4, or 5 significant figures.
The potential ambiguity in the last rule can be avoided by the use of standard exponential, or "scientific," notation. For
example, depending on whether the number of significant figures is 3, 4, or 5, we would write 50,600 calories as:
4
5.06 × 10 calories (3 significant figures)
4
5.060 × 10 calories (4 significant figures), or
4
5.0600 × 10 calories (5 significant figures).
Another potential ambiguity comes from an ending decimal
50,600. calories (5 significant figures)
The decimal makes all digits significant
How do you find how many sig.
figs. a number has?
If a decimal point is Present, ignore zeros
on the Pacific (left) side (except if there are
zeros between non-zero numbers; in this
case all are significant from the first nonzero number on). If the decimal point
is Absent, ignore zeros on the Atlantic
(right) side. Everything else is significant.
Ex:
1) 0.003200 (4 sig. figs)
2) 1.003200 (7 sig. figs)
Doing math with Sig. figs.!
Adding and subtracting: line the numbers’ decimal points
up. Add (or subtract) the numbers.
• To decide where to round, the result should have as
many decimal places as the measured number with the
smallest number of decimal places.
– Ex: 121.23 (two decimal places) + 1.2540 (four
decimal places) = 122.4840
*Answer should round based on two decimal places
which would give 122.48
Example #1
A) 13.559 + 1.22599 + 20.23=
B) 100.9552 – 29.059 ‒ 79.8 =
C) 0.98 – 0.099 – 0.422 =
Rounding to the right number of
sig. figs.
Given a value, start from the left (using the
concept of pacific ocean for decimal
numbers) and begin counting the number
of sig. figs. you are told to have.
Replace whole numbers with zeros for place
holders, decimal numbers just leave them
off.
Example #2
Round each number to three significant
digits:
1. 0.0050505
2. 123040
3. 3500
4. 2.0309
5. 1.4592
How to multiply and divide?
Multiply or divide the numbers given.
Count the number of sig.figs. in each value.
Round your answer to the number of sig. figs. that
has the least of the values.
So… if you are multiplying or dividing two values
one with 3 sig. figs. and one with 2 sig. figs.,
your answer should only have two sig. figs.
Example #3
A) 25 x 2.39 x 0.1
B) 950/0.0359
C) 7.228 x 40.3
3.4
D) 6.53 x 0.00042
Add/subtract with multiply/divide
Break into components (like operations) and
perform an order of operations. Follow individual
rules for each component.
PEMDAS (Parenthesis, Exponent, Multiplication,
Division, Addition, Subtraction)
1. Parenthesis
2. Multiply/Division
3. Addition/Subtraction
Ex: 3.2 + 2.35 x 1.560 vs. (3.2 + 2.35) x 1.560
=6.9
=8.7
Example #4
A) (0.0035 – 0.0021)
0.0245
B) 375 + 27.33 x 25
C)
4.523
(2.2 – 2.1)
D) 0.036 – 3.2/1.37
Scientific Notation
It’s the way to handle very large or small numbers.
Ex: 0.0000000000032 is a very small number
Ex: 1,231,500,000 is a very large number
To go from a number to scientific notation
1) Find the first non-zero value and place a decimal in between it and the
next number (located to the right).
2) Now, starting from your newly added decimal, count how many spaces
are between the decimal you added and the original decimal. Each space
represents a factor of 10 (why you see x 10x). If there is no decimal count
from your newly added decimal to the end of number.
3) If you move left, your exponent (superscript) x will be negative the
number of spaces counted. If you move right, your exponent (superscript) x
will be positive the number of spaces counted.
4) Keep number of sig. figs. In original value.
Scientific Notation
It’s the way to handle very large or small numbers.
Ex: 0.0000000000032 is a very small number
1) 0.000000000003.2
2) There are 12 spaces to the left
3) Left tells you x 10-12 and negative
4) There were two sig. figs. to begin with so converted value is now
3.2 x 10-12
Ex: 1,231,500,000 is a very large number
1) 1.231500000
2) There are 9 spaces to the right (end of number)
3) Right tells you x 109 and positive (we do not put +)
4) There were 5 sig. figs. to begin with so converted value is now
1.2315 x 109
* You can also work backwards from scientific notation to number. If the
exponent (superscript) is positive move that many spaces right and fill in
zeros. If exponent (superscript) is negative, move that many spaces left and
fill in zeros (keep decimal).
Example #5
A) 0.00068 (give scientific notation)
B) 1.38 x 105 (give number)
C) 585,000 (give scientific notation)
D) 6 x 10-6 (give number)
E) 695.1 x 10-4 (give standard scientific
notation; tricky)
Example #6
Sig. Figs with scientific notation. How many
sig. figs. does each number have?
A) 6.80 x 10-3
B) 1.3821 x 105
C) 3 x 108
Round each to two sig. figs.
Sig. Figs. and Actual Measurements
• The number you estimate determines the sig. figs.
You can tell this is between 2.8 and 2.9. What numbers
come between 2.8 and 2.9?
2.81, 2.82, 2.83, etc
*2.811 comes between 2.8 and 2.9 as well but in this case
you would be estimating the last two decimal places.
-In this case the hundredths place determines the sig. figs.
because it is the number you are estimating.
- Rule of thumb when taking a measurement, the number
of sig. figs. will be a tenths place to the right of the decimal
place you can actually read with a tick mark.
Practice