* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Hooke`s Law
Specific impulse wikipedia , lookup
Hunting oscillation wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Atomic theory wikipedia , lookup
Equations of motion wikipedia , lookup
Mass in special relativity wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Centripetal force wikipedia , lookup
Electromagnetic mass wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Classical central-force problem wikipedia , lookup
Work (physics) wikipedia , lookup
Seismometer wikipedia , lookup
Hooke's law wikipedia , lookup
Relativistic mechanics wikipedia , lookup
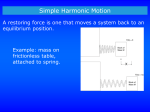
Hooke’s Law Introduction In this experiment, you will investigate Hooke’s law and simple harmonic motion and gain experience in graphical analysis. Equipment and Materials 1. Hooke’s law apparatus (spring, rod, and clamps) and slotted masses 2. Timer 3. Meter stick Important Concepts Robert Hooke was an English physicist and a contemporary of Isaac Newton. In 1678, he discovered a directly-proportional relationship between the force applied to a spring and the elongation of the spring. Consider a spring suspended vertically with its lower end at a marked position, as shown in Figure 1a. Now suspend a mass, m, from the spring, as shown in Figure 1b. Of course, the spring stretches; let’s call the distance of stretch, or elongation, d. The stretching stops when the restoring force of the spring, FS, reaches a value equal to the force of gravity, FG, on the mass, as shown in figure 1c. The mass is now in equilibrium between the two opposing, equal forces. The force of gravity, FG, on an object is known as the object’s weight, w, which can be found by multiplying the object’s mass, m, by g, the acceleration due to gravity (9.8 m/s2). (w = mg is a special case of Newton’s second law of motion, force = mass x acceleration, where w is the force and g is the acceleration.) Figure 1: (a) The suspended, unstretched spring. (b) Adding mass m causes the spring to stretch a distance d. (c) When the restoring force, FS, equals the force of gravity, FG (that is, the weight mg), the mass is in equilibrium and is stationary. (d) If the mass is doubled (to 2m), the distance of stretch also doubles (to 2d). What happens if the mass on the spring is now doubled, as shown in figure 1d? That doubles the force of gravity (to 2mg), and the distance of elongation doubles (to 2d) as the mass moves to a new equilibrium position where the force of gravity and the restoring force are again equal. A tripling of the mass results in a tripling of the distance, and so forth. In other words, the distance is directly proportional to the force applied to the spring, FG or mg, and to the restoring force FS. d ∝ FG = mg = FS To make the proportionality an equality, Hooke introduced the spring constant, k. kd = FG = mg = FS Hooke’s law is usually given in the for FS = -kd, where the minus sign indicates that the restoring force is in the opposite direction from the distance of elongation. However, you will be using it in a rearranged form of kd = mg, namely Equation 1: k mg d The spring constant is a measure of the stiffness of the particular spring (how hard it is to stretch it). The stiffer the spring, the larger the value of k. As you can see from Equation 1, k has the units of force divided by distance (N/m). (A newton, N, is equivalent to a kg m/s2.) Of course, all laws have their limitations, and Hooke’s law is no exception. There comes a point where the addition of more mass to the spring exceeds the ability of the restoring power of the spring. Then the spring distorts irretrievably or may even break; it has reached its elastic limit and no longer follows Hooke’s law. Therefore, be careful not to overload the spring. Measuring the Spring Constant Figure 1b shows a common technique to find the value of the spring constant; namely, hang the spring vertically, add a mass, and measure the displacement distance. The spring stretches a distance d from its initial position because of the weight (mg) of the mass. The upward-directed spring force (kd) must balance this downward force at equilibrium. For example, suppose a spring is stretched 0.031 m (3.1 cm) by a mass of 0.110 kg (110 g). k mg 0.110 kg x 9.8 m/s 2 =k = 35 N/m d 0.031m In this experiment, you will use six different masses to stretch the spring six different distances. You will plot these six pairs of values on a graph. The slope of the line obtained will be the average value of m/d, which you will then multiply by g to get the spring constant. Simple Harmonic Motion Suppose the mass on the end of the spring is pulled down and then released. What happens? As you know from experience, it vibrates up and down (oscillates) around the equilibrium position (Figure 2b). When the mass is below the equilibrium position (Figure 2a), the restoring force is greater than the force of gravity (the weight), and the mass tends to move up. But when the mass is above the equilibrium position (Figure 2c), the force of gravity is greater than the restoring force, causing the mass to tend to move back down. If it were not for friction, the oscillation would go on forever, with no change in the amplitude of the distance of displacement. Figure 2: (a) At the bottom of the oscillation, the restoring force FS (or kd) is greater than the force of gravity FG (or mg), and the mass moves up. (b) At the mid-point of the oscillation, FS is equal to FG,, but the object’s momentum keeps it moving up. (c) At the top of the oscillation, FG is greater than FS, and the object moves down. The time required for one round trip (from the lowest position to the highest and back to the lowest) is known as the period, symbolized T. Often, physicists speak of the frequency, f, of the oscillation. The frequency is just the number of oscillations per second. Its unit is reciprocal seconds, s-1 (also called hertz, Hz), and it is found by dividing the period into 1. Equation 2: f 1 T A situation like this, where a restoring force causes a particle to oscillate back and forth through an equilibrium position, is termed simple harmonic motion, sometimes abbreviated SHM. If a piece of paper were drawn along at a constant rate at right angles to the oscillation, the particle would trace out a wave-like cosine curve as shown in Figure 3. Such a curve is characteristic of displacement versus time for simple harmonic motion. The mid-line of the curve represents the equilibrium position. The distance from one crest to the next is the wavelength, λ (lambda). Figure 3: As the paper strip moves to the right under the oscillating mass, a wave is sketched. The greater the distance of elongation, the greater the amplitude (height and depth of the humps) of the wave. The greater the period, the longer the wavelength. Much of the motion that occurs in nature is simple harmonic motion. Because of its thermal energy, an atom in a solid vibrates around its equilibrium position with simple harmonic motion, the amplitude of which is determined by the temperature. Other examples of simple harmonic motion are a pendulum and a vibrating string of a musical instrument. All oscillating systems have a great deal in common, so what you learn about masses on springs is applicable to a variety of other situations. The criterion for simple harmonic motion is the presence of a restoring force that is proportional to the displacement. Oscillating systems provide a good example of the law of conservation of energy. Consider the oscillatingmass-on-a-spring situation. At the bottom, the energy is all in the form of potential energy due to the spring; at the top, it is all in gravitational potential energy. At points in between, the mass is moving, so some of the energy is kinetic energy. The mass will be moving fastest when it reaches the equilibrium position, so that is where the kinetic energy is at a maximum; and at that point, the total potential energy is zero, since the gravitational potential energy is cancelled by the potential energy due to the spring. (See figure 4). Figure 4: When a mass is oscillating up and down, its total potential energy is at a maximum at the top and at the bottom, and its kinetic energy is zero. At the mid-point, its, kinetic energy is at a maximum, and its total potential energy is zero. In this experiment, you will find the period of oscillation for several different masses attached to the spring. You will find that the period changes with different masses, but not in a directly proportional fashion; when you plot mass versus period, you will get a parabola, not a straight line. However, when you square the periods and plot T2 versus mass, you will get an ascending straight line, characteristic of a directly proportional relationship. The period, T, of an object in simple harmonic motion is found by Equation 3a: T 2 dis tan ce acceleration But you have seen that kd = mg. Rearranging, distance divided by acceleration, d/g, equals mass divided by the spring constant, m/k. Substituting into Equation 3a gives Equation 3b: T 2 m k 4 2 m Squaring both sides gives T . Rearranging for k gives k 2 Equation 4: k 4 2 m T2 Since the slope of the graph of mass versus T2 gives the average value of m/T T2, you can find the value of the 2 spring constant by multiplying the slope by 4π (which is 39.4). Thus, you have a second value of the spring constant, and it should be in reasonable agreement with the value found directly from Hooke’s Law. Instructions Part A: Finding the Spring Constant by Spring Elongation 1. You will use a Hooke’s law apparatus like that shown in Figure 5. Hang the spring so that the horizontal wire falls over the distance scale, which reads in cm. Place 20 g (two slotted masses) on the weight hanger. Move the sliding distance scale (pinch at the back) until the horizontal pointer is lined up. (In order to avoid parallax errors, be sure your eye is level with the pointer and scale.) You will define this point as zero mass and zero distance; so from now on, ignore the mass of the hanger and of this original 20 g. Figure 5: Hooke’s Law Apparatus 2. Add 50 g more, let the system come to equilibrium, and read the distance to the nearest 0.1 cm. Have your partner check the reading. After changing the distance to meters by dividing by 100 cm/m, record it in the data table. Note that the mass has been recorded in kg by dividing the mass in g by 1000 g/kg. 3. Repeat four times, adding 50 g each time, until the total mass is 270 g. Remove all masses as soon as you have the final reading. 4. Use graph paper to plot distance (in meters, m) on the horizontal scale and mass (in kilograms, kg) on the vertical scale. Scale each axis, starting with 0 at the origin. Use a dot inside a circle for each point. Draw the best straight line through the points. Title this plot Graph 1. Be sure to label your axes. 5. Find the slope of the line by using the values for the two points farthest apart but lying dead on the line. Show both setup and answer on the data sheet. 6. To find k, use Equation 1, multiplying the slope by g, 9.8 m/s2. Part B: Finding the Spring Constant by Simple Harmonic Motion 1. Reverse the spring so that the pointer is pointing away from the scale. This will lessen friction as the masses oscillate. 2. Add 70 g to the empty hanger. Set the timer to zero, and get ready to depress the bar to start it. With the other hand, pull down the hanger about a centimeter. As you let go, start the timer. Time to the nearest 0.1 s how long it takes for the spring to return to the bottom position 10 times. The time is a very few seconds, so because of reaction time it is best for one partner at a time to do it all. This is going to take some practice, because it is hard to keep count since the mass is oscillating very fast. Watch the bottom of the spring. Repeat at least three times for each mass until you have three readings the same. (It gets easier as you go, because the oscillation is not as fast as you add more mass, but you will need to pull down a little farter as the mass gets greater.) Your partner will repeat Part B after you are through, and you can then repeat any values on which the two of you are not in reasonable agreement. 3. Record on the data sheet the time for the 10 periods with 70 g of mass. Divide that time by 10 to get the period, T. Square T and record that value (watch significant figures). Use Equation 2 to calculate the frequency. 4. Repeat the process five more times, adding 50 g more each time (the last time add only 20 g) until the total is 290 g. You will have six values. 5. Plot the period, T ( in seconds, s) on the horizontal axis and the mass (in kilograms, kg) on the vertical axis for each of the six pairs of values. Title this Graph 2. Be sure to label your axes. 6. Draw the best smooth curve through the points. 7. Plot T2 (in seconds squared, s2) on the horizontal axis and the mass (in kilograms, kg) on the vertical axis for each of the six pairs of values. Draw the best straight line through the points and find the slope as you did in Part A. Title this Graph 3. Be sure to label your axes. 8. Use Equation 4 to find the value of k by multiplying your value of the slope by 39.4 (4p2). Your result seems to come out in kg/s2, but this multiplied by m/m shows it is equivalent to N/m, so give that latter combination as your k units. 9. Calculate the percent difference between the calculated values of k for parts A and B. Prelab Sheet for “Hooke’s Law” Section: Your Name: 1. In what year was Hooke’s law discovered? 2. Weight is found by multiplying mass by 3. What units are expected for a spring constant? 4. 6.2 cm = ________ m 85 g = __________ kg 5. Calculate the spring constant, k, for a spring that is elongated 0.060 m by a mass of 0.150 kg. Show the setup. 6. In physics, the letters SHM stand for _____________ _____________ ______________ 7. In order for an object to undergo SHM, there must be ___________________________ 8. Which one of the graphs below shows a directly proportional relationship between X and Y? The arrows on the axes point in the direction of increasing values. a. (a) (b) (c) 9. Pi, π, has a value of 3.14. How much is 4π2? 10. In Part B, if your partner operates the timer, who counts the periods? 11. What is T if it takes 4.6 s for the mass to go up and come back down ten times? What is the frequency, f? (d) Data Sheet for “Hooke’s Law” Section ______ Partner’s Last Name _____________________ Your Name ____________________ A. Finding the Spring Constant by Spring Elongation Total mass (kg) 0 0.050 0.100 0.150 0.200 0.250 Total Distance (m) Slope of Graph 1 line (∆m/∆d) Setup: Answer: ___________ Calculated value for k Setup: Answer: ____________ B. Finding the Spring Constant by Simple Harmonic Motion Total mass (kg) 0.070 0.120 0.170 0.220 0.270 0.290 Time for 10 periods (s) Period, T (s) Period Squared, T2 (s2) Frequency, f (s-1) Slope of Graph 3 line (∆m/∆T 2) Setup: Answer: ____________ Calculated value for k Setup: Answer: ____________ % Difference in the Part A and Part B k values Setup: Answer ____________