Download Unit-16-Confidence-Intervals-for

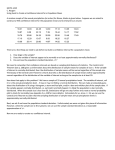
Elementary Statistics
Triola, Elementary Statistics 11/e
Unit 16 The Confidence Interval for Variation
Estimation
Unit 16 The Confidence Interval for Variation (Section 7-5)
The sampling distribution of the population variance, 𝝈𝟐 is the Chi Square distribution. This is a new
probability distribution for us. It is pictured below,
There are a few things to notice about this distribution. The most obvious is that it is not symmetrical,
but rather, skewed to the right. Another interesting point is that the left tail ends at zero. There are no
negative values along the 𝑋 2 axis. Finally, similar to the Student t distribution, the exact shape of the
Chi Square distribution depends on the degrees of freedom which equal one less than the sample size.
The symbol for the Chi Square variable is 𝑋 2 . This is not X squared. The superscript is just part of the
notation. Because the distribution is not symmetrical, we can’t come up with interval expression like
𝑠 2 ± 𝐸. Instead, we find a left critical value, 𝑋𝐿2 that has an area under the curve to the left of it equal to
𝛼⁄ and a right critical value, 𝑋 2 , that has an area under the curve to the right of it equal to 𝛼⁄ . See
𝑅
2
2
the figure below,
This figure illustrates the situation when we are calculating a 95% confidence interval for a sample of
size 10. The degrees of freedom is 9 and the areas that are shaded red sum to 𝛼 = 0.05.
There is no margin of error when calculating confidence intervals for variances. There is only an upper
bound and a lower bound as shown by the following expression for the interval,
57
Elementary Statistics
Triola, Elementary Statistics 11/e
Unit 16 The Confidence Interval for Variation
(𝑛 − 1)𝑠 2
(𝑛 − 1)𝑠 2
√
√
<
𝜎
<
𝑋𝑅2
𝑋𝐿2
Notice a few things here. First, the only information that you need from the sample is its size and its
standard deviation, s. Also notice that 𝑋𝑅2 is on the left side of the expression and 𝑋𝐿2 is on the right.
This makes sense since they are in the denominators and 𝑋𝑅2 > 𝑋𝐿2 .
When we calculated the confidence interval for means, we used T.INV.2T to find the critical value. This
Excel tool is a two-tail tool and we only need one critical value, 𝑡𝛼⁄2 because the Student t distribution is
symmetrical. This is not the case here. We will need to find two critical value, 𝑋𝑅2 and 𝑋𝐿2 , and we will
need two separate Excel tools to do so, CHISQ.INV.RT and CHISQ.INV respectively.
Remember, variation, 𝜎 2 , is simple the square of standard deviation, 𝜎.
Worked Example
Let’s say that we want to estimate variation of the weight of U.S. quarters. We collect a simple random
sample of 30 quarters, weigh them and calculate the standard deviation of the sample, 𝑠 = 4.7 gm. It’s
our goal to calculate the 95% confidence interval for the population standard deviaiton, 𝝈.
𝛼
𝛼
We will need to calcualte 𝑋𝐿2 . The area to the left of 𝑋𝐿2 is 2 where 𝛼 = 1.0 − .095 = 0.05. Hence , 2 =
0.05. We use CHISQ.INV to find 𝑋𝐿2 ,
58
Elementary Statistics
Triola, Elementary Statistics 11/e
Unit 16 The Confidence Interval for Variation
In a similar fashion, we find 𝑋𝑅2 ,
Here is an excel spreadsheet for this example. If you double click on the cells below, you will open Excel
and you can explore the contents of the cells.
s
n
4.7
XL
XR
LB
UB
30 16.04707 45.72229 3.743113 6.318281
The confidence interval is thus given by,
3.7431 < 𝜎 < 6.3183
This is the end of Unit 16. In class, you will get more practice with these
concepts by working exercises in MyMathLab.
59