Download Using Excel to Create Confidence Intervals for One Population Mean

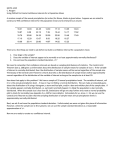
MATH-1410
C. Haugen
Using Excel to Create a Confidence Interval for a Population Mean
A random sample of the annual precipitation (in inches) for Nome, Alaska is given below. Suppose we are asked to
construct a 95% confidence interval for the population mean and to interpret our answer.
18.31
14.93
24.38
14.30
17.13
13.05
13.43
19.87
9.08
22.15
7.39
10.44
14.17
17.62
19.76
20.66
24.25
20.09
22.06
15.46
17.49
17.10
12.29
13.67
9.93
19.25
16.27
19.06
20.14
20.80
14.97
14.92
15.23
There are a few things we need to ask before we build a confidence interval for a population mean.
1. How large is the sample?
2. Does the variable of interest appear to be normally or at least approximately normally distributed?
3. Do we know the population standard deviation,  ?
We need to remember that confidence intervals are based on sampling distributions of statistics. The Central Limit
Theorem (see p. 268) gives us information about the distribution of sample means for samples of size n. If the variable
of interest is normally distributed, then the distribution of sample means will be normal regardless of the sample size.
The beauty of the Central Limit Theorem is that it also tells us the distribution of sample means will be approximately
normal regardless of the distribution of the variable of interest as long as the sample size is at least 30.
How does that apply to this problem? We have a sample of 33 annual precipitation levels. The variable of interest, call
it X, is the annual precipitation level. X may or may not follow a normal distribution. We can make an educated guess
about the distribution of X using a histogram, a stem-and-leaf plot, and/or a box-and-whisker plot of the sample data. If
the sample appears normally distributed, i.e. symmetric and bell-shaped, it is likely the population is also normally
distributed. When the sample size is less than 30, Statisticians will go one step further and create a normal probability
plot to check for normality (see Appendix C p. A28 for more details). Fortunately for us, since n = 33, we can use the
Central Limit Theorem to claim that the sampling distribution of sample mean annual precipitation levels is
approximately normally distributed.
Next, we ask if we know the population standard deviation. Unfortunately we were not given this piece of information.
However, when the sample size is 30 or greater, we can use the sample standard deviation as a reasonable
approximation of  .
Now we are ready to create our confidence interval.
1. Open a new Excel Workbook and enter the sample data in the first or second column. Unfortunately, Excel does
not have a built-in function that will create confidence intervals for us. Instead, we will have Excel calculate the
margin of error of our estimate and then use it locate the left and right endpoints of the confidence interval.
Before we ask Excel to calculate the margin of error, we need three pieces of information: the size of the
sample, the sample standard deviation, and α (Greek letter alpha). Alpha is a number related to our confidence
level. If we let c represent the confidence level, alpha is defined as 1 – c. So, for example, if we want to build a
90% confidence interval, c would be 0.90 and α would be 1 – 0.90 or 0.10.
We know our sample size is 33. To find the sample standard deviation, we could have Excel calculate the
summary statistics of our data set (click on the Using Excel to Calculate Summary Statistics link on my website
for more details). Since we want to build a 95% confidence interval estimate for the mean, we know α = 1 – 0.95
=0.05.
2. Before we move forward, it would probably be a good idea to click on an open cell. Excel will store the result of
the next calculation there, so it would help to click somewhere away from the data set and the summary
statistics. I happened to pick cell G3. Once you’ve done that, click on the Formulas tab, then on More Functions
in the Formulas ribbon, and then select Statistical. A list of statistical functions should appear. We need to
make our way down to CONFIDENCE.NORM.*
*Note: If we needed to create a t-interval estimate for the population mean, we would select CONFIDENCE.T
and then proceed to the next step.
Once we click on CONFIDENCE.NORM, a dialog box should appear:
We are asked for the three pieces of information I mentioned earlier. We already know α = 1 – 0.95 = 0.05.
From the summary statistics, we know the sample standard deviation is 4.234554979 and the sample size is 33.
Click on the OK button and the margin of error will appear in cell G3 (or wherever you clicked earlier).
3. Next, we will use the margin of error to calculate the left and right endpoints of our confidence interval. Since
𝑥̅ − 𝐸 < 𝜇 < 𝑥̅ + 𝐸, we can ask Excel to subtract the margin of error from the sample mean…
…and then add the margin of error to the sample mean:
The endpoints of the interval are shown below:
The last step is to interpret our results:
We are 95% confident that the mean annual precipitation in Nome, Alaska is somewhere between 15.211 and
18.101 inches.