Download Five-Minute Check (over Lesson 5–2) CCSS Then/Now Key

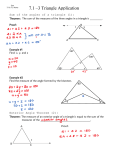
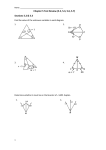
12/1/2015
Five-Minute Check (over Lesson 5–2)
CCSS
Then/Now
Key Concept: Definition of Inequality
Key Concept: Properties of Inequality for Real Numbers
Theorem 5.8: Exterior Angle Inequality
Example 1: Use the Exterior Angle Inequality Theorem
Theorems: Angle-Side Relationships in Triangles
Example 2: Order Triangle Angle Measures
Example 3: Order Triangle Side Lengths
Example 4: Real-World Example: Angle-Side Relationships
1
12/1/2015
Over Lesson 5–2
Find the coordinates of the centroid of the triangle
with vertices D(–2, 9), E(3, 6), and F(–7, 0).
Find the coordinates of the orthocenter of the
triangle with vertices F(–1, 5), G(4, 4), and H(1, 1).
___
(3-4)___
In ∆RST, RU is an altitude
and SV is a median.
Find y if m∠
∠RUS = 7y + 27.
Find RV if RV = 6a + 3 and RT = 10a + 14.
What is the center of gravity of a triangle named?
Over Lesson 5–2
Find the coordinates of the centroid of the triangle
with vertices D(–2, 9), E(3, 6), and F(–7, 0).
A. (–4, 5)
B. (–3, 4)
C. (–2, 5)
D. (–1, 4)
2
12/1/2015
Over Lesson 5–2
Find the coordinates of the orthocenter of the
triangle with vertices F(–1, 5), G(4, 4), and H(1, 1).
A.
B.
C. (2, 3)
D.
Over Lesson 5–2
___
___
In ∆RST, RU is an altitude and SV is a median.
Find y if m∠
∠RUS = 7y + 27.
A. 5
B. 7
C. 9
D. 11
3
12/1/2015
Over Lesson 5–2
___
___
In ∆RST, RU is an altitude and SV is a median.
Find RV if RV = 6a + 3 and RT = 10a + 14.
A. 3
B. 4
C. 21
D. 27
Over Lesson 5–2
Which of the following points is the center of
gravity of a triangle?
A. centroid
B. circumcenter
C. incenter
D. orthocenter
4
12/1/2015
Content Standards
G.CO.10 Prove theorems about triangles.
Mathematical Practices
1 Make sense of problems and persevere in
solving them.
3 Construct viable arguments and critique
the reasoning of others.
You found the relationship between the angle
measures of a triangle.
• Recognize and apply properties of
inequalities to the measures of the angles of
a triangle.
• Recognize and apply properties of
inequalities to the relationships between the
angles and sides of a triangle.
5
12/1/2015
6
12/1/2015
Use the Exterior Angle Inequality Theorem
Exterior Angle Inequality
∠14 > ∠4
∠9 > ∠6
∠14 > ∠11
∠9 > ∠7
∠14 > ∠2
∠14 > ∠3 + ∠4
Vertical Angles
∠14 > ∠11 = ∠9
Definition of
Inequality
∠14 > ∠3
Answer: Thus m∠14 is greater than m∠2, m∠3, m∠4,
m∠6, m∠7, m∠9, and m∠11
Use the Exterior Angle Inequality Theorem
Exterior Angle Inequality
Vertical Angles
∠10 > ∠5
∠16 > ∠10 > ∠5
∠15 > ∠12 > ∠5
∠17 > ∠5 + ∠6
∠12 = ∠10 > ∠5
Definition of
Inequality
∠17 > ∠5
Answer: Thus m∠5 is less than than m ∠ 10, m∠12,
m∠15, m∠16, and m∠17
7
12/1/2015
A.
B.
C.
D.
A.
B.
C.
D.
8
12/1/2015
Summary:
1. The longest side is across
from the largest angle.
2. The largest angle is across
from the longest side.
Order Triangle Angle Measures
List the angles of ∆ABC in order from smallest to
largest.
Recall:
The largest angle is across
from the longest side.
Answer: ∠C, ∠A, ∠B
9
12/1/2015
List the angles of ∆TVX in
order from smallest to largest.
A. ∠X, ∠T, ∠V
B. ∠X, ∠V, ∠T
C. ∠V, ∠T, ∠X
D. ∠T, ∠V, ∠X
Order Triangle Side Lengths
List the sides of ∆ABC in order from
shortest to longest.
Recall:
The longest side is across
from the largest angle.
Answer: AC, AB, BC
10
12/1/2015
List the sides of ∆RST in order from
shortest to longest.
A. RS, RT, ST
B. RT, RS, ST
C. ST, RS, RT
D. RS, ST, RT
Angle-Side Relationships
HAIR ACCESSORIES Ebony is following directions
for folding a handkerchief to make a bandana for
her hair. After she folds the handkerchief in half, the
directions tell her to tie the two smaller angles of
the triangle under her hair. If she folds the
handkerchief with the dimensions shown, which
two ends should she tie?
Recall:
The largest angle is across
from the longest side.
Answer: So, Ebony should tie the ends marked
Y and Z.
11
12/1/2015
KITE ASSEMBLY Tanya is
following directions for making a
kite. She has two congruent
triangular pieces of fabric that
need to be sewn together along
their longest side. The directions
say to begin sewing the two pieces
of fabric together at their smallest angles. At which
two angles should she begin sewing?
A. ∠A and ∠D
B. ∠B and ∠F
C. ∠C and ∠E
D. ∠A and ∠B
12