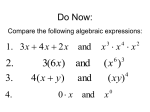* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Doc Hoyer`s
Bra–ket notation wikipedia , lookup
Abuse of notation wikipedia , lookup
Elementary mathematics wikipedia , lookup
Location arithmetic wikipedia , lookup
Positional notation wikipedia , lookup
History of mathematical notation wikipedia , lookup
Musical notation wikipedia , lookup
NAME_____________________DATE_____________PERIOD_______
Exponents
Exponents are a way to show how many times something is multiplied by itself. The small
superscript number is the number of times you multiply the number below it by itself
Examples:
42 =
4 x 4 = 16
43 =
4 x 4 x 4 = 64
28 =
2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 256
Laws of Exponents (Always write as positive exponent)
Law
x1 = x
x0 = 1
x-n = 1/xn
xmxn = xm+n
xm/xn = xm-n
(xm)n = xmn
x-n = 1/xn
Example
61 = 6
70 = 1
4-2 = 1/42
2223 = 22+3 = 25
46/42 = 46-2 = 44
(32)3 = 32×3 = 36
5-3 = 1/53
a) 35 ______
b) (-2)4 ______
c) 31 ______
d) 53______
e) 2-10______
f) 12300 _____
g) -23_____
h) 5452______
i) 737-5 _______
j) 53 ÷ 52_____
k) 28 ÷2-3______
k) (32)3_______
1
l) (4-2)3________
m) (83)-5_______
n) -120________
Scientific Notation
The number before the “x (multiplication)” is called the coefficient and must be a number
between 1 and 10. The number after the “x (multiplication)” is called the base.
For example, 1 x 109
coefficient = 1
Standard to Scientific Notation
EX 1:
1500 = 1.5 x 103
base = 10 exponent = 9
1.500
{If you make the coefficient 3 powers of 10 smaller (1500 to 1.5) than you must make the
exponent 3 powers of 10 higher}
Scientific to Standard
EX 2:
4 x 105 = 400,000 4.00000
{If you make the exponent 5 powers of 10 smaller (5 to 0) than you must make the coefficient
5 powers of 10 larger (4 to 400,000)}
2) 17,000 = __________
3) 1.7x 106 =
4) 9 x 10-5 = _____________ 5) 43,800,000 = ____________
_____________
6) 7 x 1012 =
1) 1000 = _________
_____________
7) 226,000,000 = ___________ 8) 0.823 =____________________ 9) 0.00467 = _________
Writing numbers in correct SN form
12.53 × 104 = 1.253 ×104+1 = 1.253 ×105 (number gets small; exponents becomes larger)
127.53 × 10-4 = 1.2753 × 10-4 +2 =1.2753 × 10-2
0.0067 × 105 = 6.7 × 105-3 = 6.7 × 102 (number gets big; exponents becomes smaller)
0.012 × 10-3 = 1.2 × 10-3-2 = 1.2 × 10-5
a) 72.35 × 108 =
b) 346.026 × 10-5 = ____________
2
c) 0.0023 × 108 =
d) 0.305 × 10-4 =____________
Multiplying Numbers in Scientific Notation
When you multiply numbers in scientific notation you multiply the coefficients (the numbers
before the “x”) and you add the exponents. (make sure the answer is in scientific notation)
1) (2 x 103) (4 x 106) = 8 x 109
multiply coefficients [2 x 4 = 8] and add exponents [3 + 9 = 12]
2) 5 x 103 (4 x 103) = 20 x 106 = 2.0 x 107
{coefficients; 5 x 4 = 20} & {exponents; 3 + 3 = 6}
3) 2 x 107 (5 x 104)
{coefficients; 2 x 5 = 10} & {exponents; 7 + 4 = 11}
= 10 x 1011 = 1 x 1012
1) (3 x 103 ) (2 x 104) = ____________
2) (5.7 x 107) (1.5 x 10-4) = ____________
3.) (2 .8x 10-9 )(4.75 x 10-3) = ____________
4) (6 x 10-3 )(4 x 105) = _________________
5) (7.5 x 105) (5.3 x 102) = _____________
6) (3.2 x 10-5) )(4.9x 105) = _______________
Dividing Numbers in Scientific Notation
When you divide numbers in scientific notation you divide the coefficients (the numbers before
the “x”) and you subtract the exponents .(make sure the answer is in scientific notation)
Ex.: 6 x 106 = 3 x 102
2 x 104
Ex
8 x 106 = 4 x 10-2
2 x 108
{Divide coefficients [6/2 = 3] and subtract exponents [6 - 4 = 2]}
{divide the coefficients [8/2 = 4] and subtract the exponents [6 - 8 = -2]}
1. 8.4 x 109 = __________
3 x 104
2. 9 x 107 = __________
4.2 x 105
3. 7 x 108 = __________
1 x 107
4. 2 x 103 = __________
3.5 x 103
5. 6 x 104 = __________
3 x 108
6. 9 x 104 = __________
3 x 106
3
Adding/Subtracting Numbers in Scientific Notation
Step 1 – Rewrite so the exponents are the same
Step 2 - add/subtract the decimal
Step 3 – Bring down the given exponent on the 10 (make sure the answer is in scientific
notation)
It is usually easier to change the number with the lowest exponent to the higher exponent to
the higher exponent since it represents only a small fraction of the larger number.
Ex1:
Ex 2:
2 x 103 + 4 x 102 = 2 x 103 + 0.4 x 103 [To raise 4 x 102 one power of 10 to 3 you must reduce the
= 2.4 x 103
coefficient by one power of 10]
5 x 107 + 3 x 109 = 0.05 x 109 + 3 x 109 [To raise 5 x 107 two powers of 10 to 9 you must reduce the
= 3.05 x 109
coefficient by two powers of 10]
1) 3 x 108 + 5 x 108 = _______________
2) 6.7 x 107 + 2.4 x 108 = _______________
3) 8.7 x 108 + 6.3 x 105 = _______________
4) 4.5 x 107 + 5.2 x 103 = _______________
5) 8 x 103 + 6 x 105 = _______________
6) 3.2 x 106 - 2 x 106 = _____________
Ex 1:
4 x 107 - 2 x 106 = 4 x 107 - 0.2 x 107 [To raise 2 x 106 one power of 10 to 7 you must reduce the
= 3.8 x 107
coefficient by one power of 10]
Ex 2:
8 x 105 - 5 x 103 = 8 x 105 – 0.05 x 105 [To raise 5 x 103 two powers of 10 to 5 you must reduce the
= 7.95 x 105
coefficient by two powers of 10]
1) 9 x 108 - 3 x 108 = _______________
2) 6.8 x 1010 - 4 .9x 108 = _______________
3) 8 .7x 107 - 2.3 x 104 = _______________
4) 7 x 104 - 8 x 103 = _______________
4