Download MPM 1D - bell231

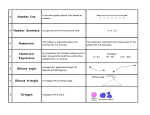
MPM 1D
Geometry
Group 1
1. Explain why a triangle cannot have two obtuse interior angles
2. Draw an example of a quadrilateral with each of set of interior angles, or
explain why the quadrilateral is not possible.


Four obtuse angles
One obtuse angle and two right angles
3. Are all regular polygons convex? Justify your answer.
4. Draw and label an example of each shape, or explain why it is not possible.


A triangle with one acute exterior angle
A quadrilateral with three obtuse angles
Group 2
1. Can a triangle have three obtuse exterior angles? Justify.
2. Draw an example of a quadrilateral with each of set of interior angles, or
explain why the quadrilateral is not possible.


Exactly two obtuse angles
One obtuse angle and three acute angles
3. Does the formula for the sum of the interior angles apply for concave
polygons? Explain your reasoning.
4. Draw and label an example of each shape, or explain why it is not possible.


A triangle with two right angles
A pentagon with two obtuse angles and three acute angles
Group 3
1.
What is the minimum number of angles you need to measure to calculate
the measure of all of the interior and exterior angles of a quadrilateral?
Justify your answer.
2. Draw an example of a quadrilateral with each of set of interior angles, or
explain why the quadrilateral is not possible.


Exactly two obtuse angles
Exactly three right angles
3. Can you determine the number of sides a polygon has from the sum of its
exterior angles? Explain your reasoning.
4. Draw and label an example of each shape, or explain why it is not possible.


A quadrilateral with four equal sides
A convex hexagon with five acute angles